Kostenloser Gleichungen Rechner – Schritt-für-Schritt Mathematikrechner
Der kostenlose Gleichungen Rechner löst lineare, quadratische und Gleichungssysteme aus Text oder Bild. Er enthält Grafiken, Wurzeln und alternative Formen.
![\sqrt[x]{y}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIwAAACgCAYAAADeroRzAAAACXBIWXMAABYlAAAWJQFJUiTwAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAATSSURBVHgB7d1daNVmHMfxbIyN9Wa2qwwZkx633XTOdgjqhjuV7tbNrmed4MV0yvCwDXchbAi+rGtB5nBjxU2FTa3vihVFby22CiqCtlV7IeLxBRGxVL2p6I3KP0kxsW3yT+JJPPl+bv59cpJyWprfeZ4nyVPDAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAJLuJcWej4wkeqT4GRDaywag8IqhtPd8MoLm68kESxxIGKjwBwMV/mCgou7DlLqKd6ukkzZ4+YqRKj5HmyQMVEgYS8exTkmWXLbewOhIGKiQMJZt7Vsd7SUtq6S2LW9mwucpJAxU1NeSEjfTG/Ja0sDDIfmBKl8rc2wvDN6WmikfT8I8hYSBSur7MOs3b3K0ZzXOkUqyjIyEgUrq+zDumd2O7k6puU/rSZgRkDBQSW0fpu96QZJlysSMuWHcG1JIlrGRMFBJbcKsbG52tOcvXCC1fe3fhi9JvcfZr4B9PxIGKqkbJQ3P7E5429wweEeKemY3Yb8Pv8KOLkkYqKSuD7Pv8CHzCytZauvrpDKz6w8JA5XUJczGf9c72vkfvjfrkS4D3kgYqKQmYQp3bstwJlMx3txgzex+NftzqXkDfpAwUElNwvza2upoN+S+lFr5ahmjIwUSBirpmel9s9x849b8S9+1gtQp72SCJQwzvYC3ku/DbNi/RyIgn5sr7cxHNVIDJ0vKkTBQKfmE2b1jp6O9cPF3Ulcs/tGAHgkDlZIdJT0zs2sZeDAkNfT8C6MkwFvJ9mH++medo92waIFUZnbDIWGgUrIrgbufaOw+3ys1+0FNNAlDHwbw5r8P84Ks6e9eq25c1USpkSVLypEwUCm5UZJ7rbpvFn0rtW15s4HwSBiolMznetHXqmOUBHiLvA9jn+ktf6yRdjabldrf3y/1yVXi55JqrFVXHCQMVCI7++xkmTpturSv9p5z7lBRLqVw6aLUqM/8oq9VRx8G8Ba6D2Mny7SPP5H2cLKUvW7Woftmte7Wb2xqMqLEWnXFRcJAJXDCuJPl8pkeqfZd+dt2bJc6s/pDx3FnjxyV2rJxnRwfdtQUeq06qJAwUFGf3V7JcvrkCan2nW1LWlfJ/m0rXNdyrFHTwM0bjv217yP0WnVBMUoCvKn7MF2nTkr1Shbbyp9/kbr1/81S7165Zr5gJULTvHlGEKxVFw8SBiqBz0b7zra66TOk7dUH6b7QK/tnJ9eM/P2UM7OTptbK97OTbkPHHqn5xrnFSRj6MIC3on/ez1/6k5yS7X+65kl8jppGW6tu4NbNMY+LHAkDeCv6Pb1rV6+W2r5pi7nh7j2zWqOdpcuWjXk8a9XFi4SBSmxnpfv5IbdRn1SMeq26oOjDAN5iey7Jnm+ZlZsjp+jR/Qcdrzd8Yd6Ta18zsmd2WasuXiQMVGJ/8nHfrl1SK9+aYG6wRk32vbm/rfldat/ZHsdxrFUXDxIGKon5/B++Ay/vLzEiW6suKEZJgLfEjTBqP6uTU7ans2vE1+216g78tyXe987/rQa8JS5hhq9GT3rP3GBfa7IcPnFc6uwZM5l/iQEJA5XEnqX2qKm6ulra71eZTzYysxsvEgYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMCnx7casgoVoq9MAAAAAElFTkSuQmCC)
![\text{[x]}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIwAAACgCAYAAADeroRzAAAACXBIWXMAABYlAAAWJQFJUiTwAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAGXSURBVHgB7d09ThtRAEbRB6FLUiVNlD5VSsRSWCQ7QaKkYguYJYCRDBUF6PIzzMPnSNY0lmWNrz49VzMGAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAwk4OxlIOxHa+xXfA7rtHK7tvhgGC1wXz/+2f32ns/fzy8VsLCkHzeGWbfzybvbaH7a2FIjsasXvvvYa0mWVwLQzLvwjw6u5x7aE7/z3WUszAkgiERDIlgSARDIhgSwZAIhkQwJIIhEQyJYEgEQyIYEsGQCIZEMCSCIREMiWBIBEMiGBLBkAiGRDAkgiERDIlgSARDIhgSwZAIhkQwJIIhEQyJYEgEQyIYEsGQCIZEMCSCIREMiWBIBEMiGBLBkAiGRDAkgiERDIlgSARDIhgSwZAs99Dkp0+yf+uT4J9+3uze+35sP+a3tTAkR2NW2zHXI+W/CAtD8nkL88IZ5N/J8e56dX6x30uysrOahSFZfmEOHxu9u3v2bZvNZtB9+/1rd729vhkfwcIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB8YfdjnSIL80RMvQAAAABJRU5ErkJggg==)
Was ist eine Gleichung?
Eine Gleichung ist eine mathematische Aussage, die Unbekannte enthält. Das Lösen von Gleichungen bedeutet,
die Werte der Unbekannten zu finden, indem eine Beziehung zwischen bekannten und unbekannten Größen
hergestellt wird. Zu den häufigsten Arten von mathematischen Gleichungen gehören lineare Gleichungen,
quadratische Gleichungen, trigonometrische Gleichungen, logarithmische Gleichungen und kubische
Gleichungen.
Gleichungen sind in Mathematik, Physik, Ingenieurwesen und Wirtschaftswissenschaften von
zentraler Bedeutung. Sie sind leistungsstarke Werkzeuge zur Lösung realer Probleme und zum Verständnis
komplexer Systeme.
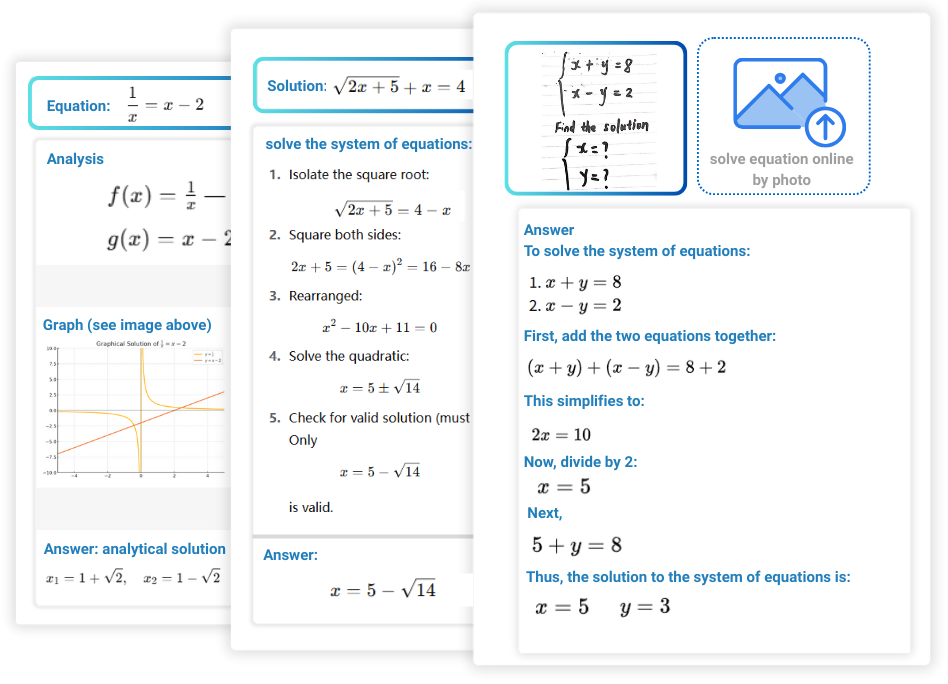
Was ist ein Gleichungsrechner?
Ein Gleichungsrechner ist ein KI-gestütztes Tool zur Lösung von mathematischen Gleichungen. Es analysiert Eingaben mithilfe von Algorithmen, um verschiedene Arten von Gleichungen und Gleichungssystemen schnell und genau zu lösen. Benutzer können Gleichungen eingeben oder Fotos mit Gleichungen hochladen. Der Decopy AI-Gleichungslöser erkennt automatisch den Inhalt, wendet standardisierte Lösungsverfahren an und zeigt die schrittweise Lösung an.
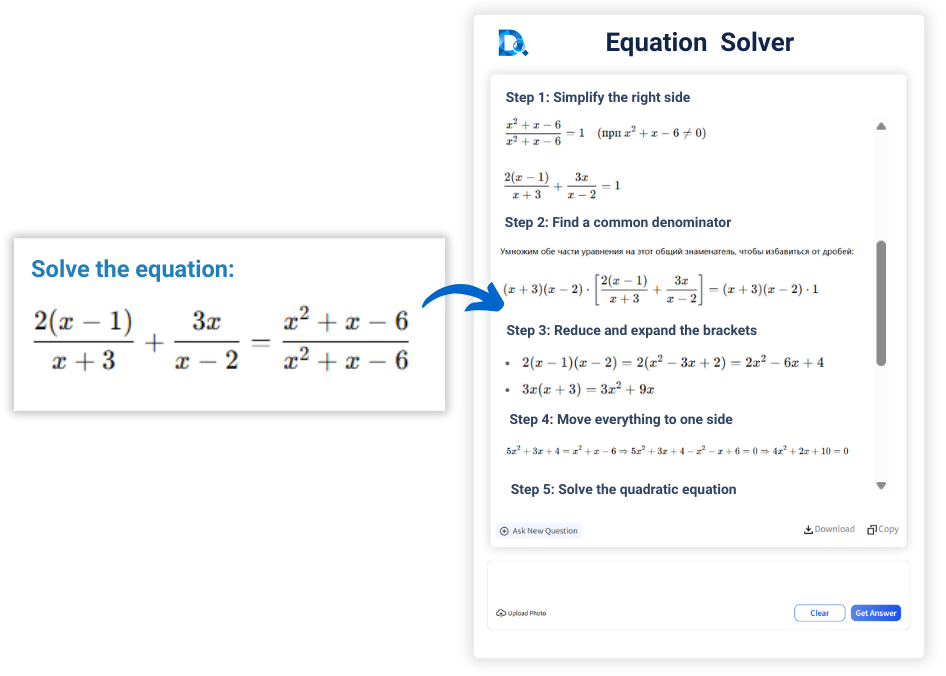
Wie löst man Gleichungen?
Traditionell erfordert das Lösen von Gleichungen manuelle Vorbereitungen, Umformungen und Berechnungen,
wie zum Beispiel Faktorisierung, Verwendung des Diskriminanten oder die Anwendung der Gauß-Elimination.
Für Gleichungen höheren Grades oder komplexe nichtlineare Systeme sind fortgeschrittene mathematische
Methoden und numerische Techniken erforderlich.
Mit einem Online-Gleichungsrechner können Sie
einfach ein Foto der Formel hochladen oder sie direkt eingeben. Der KI-gestützte
Mathematik-Gleichungslöser liefert schnell präzise Antworten. Um den Prozess verständlicher zu machen,
simuliert der Decopy AI-Gleichungsrechner menschliche Lösungsverfahren – wie Elimination, Substitution
oder die quadratische Formel – und zeigt alle schrittweisen Lösungen an.
Wie funktioniert der Decopy AI-Gleichungsrechner?
Der Decopy AI-Gleichungsrechner wird von einer fortschrittlichen KI-Mathematik-Engine betrieben, die
Algebra, numerische Analyse und algorithmische Optimierung kombiniert.
Wenn Benutzer
mathematische Gleichungen eingeben oder hochladen, erkennt das System automatisch den Gleichungstyp (wie
lineare Gleichungen, quadratische Gleichungen, trigonometrische oder logarithmische Gleichungen) und wählt
entsprechend die beste Lösungsmethode aus:
Für lineare Gleichungen und Gleichungssysteme
verwendet es die Gauß-Elimination oder Matrixmethoden für schnelle Lösungen.
Für quadratische
Gleichungen wendet es die diskriminantenbasierte quadratische Formel an, um die Lösung Schritt für Schritt
zu finden.
Für trigonometrische, logarithmische und kubische Gleichungen nutzt es
Standardumformungen, Faktorisierungen oder numerische Annäherungen.
Für komplexe nichtlineare Systeme werden numerische Methoden oder fortgeschrittene Lösungsverfahren
angewendet.
Dieser Gleichungslöser liefert die Endergebnisse und zeigt schrittweise Lösungen,
um den Benutzern zu helfen, die mathematischen Prinzipien zu verstehen.
Funktionen des Gleichungsrechners
Lösen Sie mathematische Gleichungen schnell und genau online, indem Sie Fotos hochladen oder manuelle Eingaben vornehmen. Unterstützt alle Gleichungstypen mit einer schrittweisen Analyse.
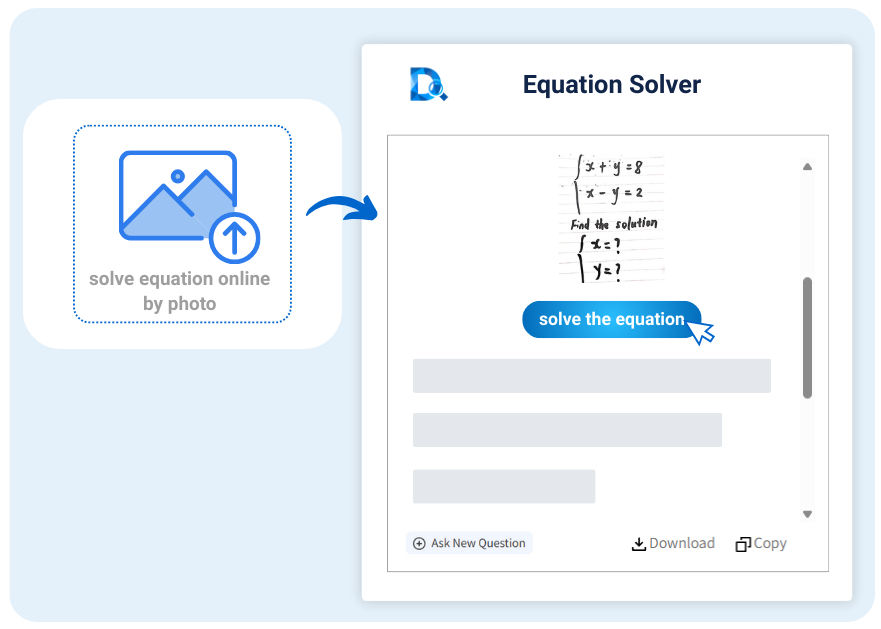
Foto-Lösung
Manuelle Eingabe
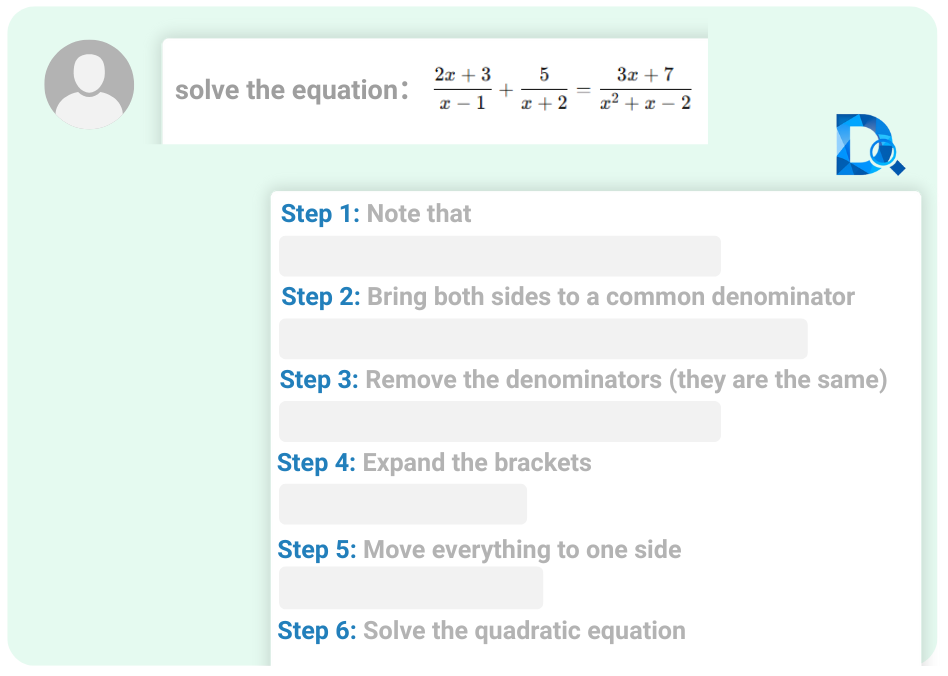
Schritt-für-Schritt Lösungen
Unterstützung für verschiedene Gleichungstypen
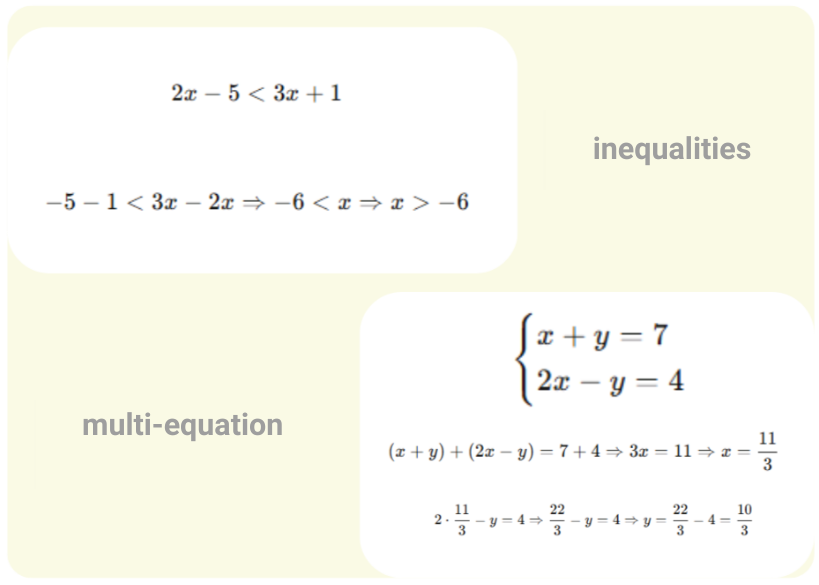
Ungleichungen und Gleichungssysteme lösen
Mobil-optimiert
Ein jederzeit und überall zugänglicher Mathematischer Gleichungsrechner
Ein mobiler, benutzerfreundlicher Online-Gleichungsrechner, der sowohl Foto- als auch manuelle Eingaben unterstützt und eine schrittweise Analyse bietet.
Schüleraufgaben
Prüfungsvorbereitung
Unterstützung im Unterricht
Komplexe Überprüfung
Lehrbewertung
Selbststudium
Unterstützte Typen von Gleichungen
Unser Gleichungsrechner kann die folgenden Arten von mathematischen Gleichungen lösen. Egal wie komplex, Sie erhalten eine detaillierte, schrittweise Lösung.
| Typ der Gleichung | Allgemeine Form | Lösungsmerkmale |
|---|---|---|
| Lineare Gleichungen | ax + b = 0 | Eine Wurzel, gelöst durch Umstellen und Teilen |
| Quadratische Gleichungen | ax² + bx + c = 0 | Quadratische Formel, bis zu zwei Lösungen |
| Biquadratische Gleichungen | x⁴ + bx² + c = 0 | gelöst durch Variablensubstitution |
| Polynomgleichungen | aₙxⁿ + ... + a₀ = 0 | Bis zu n reelle oder komplexe Wurzeln |
| Logarithmische Gleichungen | log_b(f(x)) = g(x) | gelöst durch Umformen in f(x) = b^g(x) |
| Exponentielle Gleichungen | a^{f(x)} = b^{g(x)} | Logarithmische Transformation beider Seiten |
| Radikale Gleichungen | √f(x) = g(x) | Beide Seiten quadrieren und Domain überprüfen |
| Absolute-Wert-Gleichungen | |f(x)| = g(x) | Zwei Fälle: f(x)=g(x) und f(x)=–g(x) |
| Trigonometrische Gleichungen | sin(x), cos(x), ... | Verwendung von Periodizität und Identitäten |
| Komplexe Gleichungen | f(z) = 0 | Lösungen in der komplexen Ebene |
| Matrixgleichungen | AX = B | Lineare Algebra Methoden, inverse Matrizen |
| Rationale Gleichungen | P(x)/Q(x) = 0 | Überprüfung des Definitionsgebietes und Finden rationaler Wurzeln |
| Floor-Funktion-Gleichungen | ⌊f(x)⌋ = g(x) | gelöst innerhalb ganzzahliger Intervalle |
| Wurzel-basierte Konstruktion | f(x) = (x − r₁)... | Polynom aufbauen aus bekannten Wurzeln |
| Punkt-basierte Konstruktion | f(x) durch (x₁, y₁)... | Interpolationsmethoden |
| Numerische Methoden | f(x) = 0 | Approximative Wurzelsuche (z.B. Newtonsche Methode) |
| Differentialgleichungen | y', y'' = f(x) | Finden der Funktion y(x) via Lösungsmethoden |
So verwenden Sie den Decopy AI Gleichungsrechner?
- 1
Öffnen Sie die Website und gehen Sie zur Seite des Gleichungsrechners.
- 2
Laden Sie ein Foto hoch oder geben Sie Ihre Gleichung direkt ein.
- 3
Klicken Sie auf „Lösen starten“ und das System wird die Gleichung automatisch analysieren.
- 4
Sehen Sie sich die schrittweise Lösung an oder stellen Sie Folgefragen.
Wer nutzt den Online-Gleichungsrechner?
Lösen Sie mathematische Gleichungen schnell und präzise – von der Grundschule bis zur Universität. Der Rechner unterstützt standardisierte Tests und staatliche Prüfungen.
Grundschüler
Fördert frühes mathematisches Denken in Algebra und einfachen Gleichungen.
Sekundarstufe I und II
Hilft bei der Vorbereitung auf Prüfungen in Algebra, Funktionen und Trigonometrie.
Studierende
Ideal für höhere Mathematik und komplexe Gleichungen in Kursen wie Analysis und Linearer Algebra.
Selbstlernende Erwachsene
Unterstützt Erwachsene beim Entwickeln von mathematischem Denken und logischer Strukturierung.
Lehrkräfte und Tutoren
Erleichtert die Unterrichtsplanung mit standardisierten Lösungen und der Analyse von Schülerantworten.
Internationale Studierende
Deckt mathematische Abschnitte in internationalen Aufnahmeprüfungen und standardisierten Tests ab.
Warum unseren Gleichungsrechner verwenden
100 % kostenlos
Keine Anmeldung, keine Werbung und absolut keine versteckten Kosten. Beginnen Sie sofort mit dem Lösen von Mathematikaufgaben online.
Präzise und zuverlässig
Angetrieben von einem intelligenten Algorithmus löst der Decopy AI-Gleichungslöser alle Arten von Mathematikaufgaben exakt.
Einfach und effektiv
Selbst Anfänger können mit diesem Rechner problemlos mathematische Gleichungen lösen.
Mehrsprachige Unterstützung
Dieser Rechner erkennt mathematische Gleichungen in acht verschiedenen Sprachen, was ihn für internationale Prüfungen geeignet macht.
Keine Installation erforderlich
Der Gleichungsrechner funktioniert direkt in Ihrem Browser und benötigt keine App-Installation.
Unterstützung aller Gleichungstypen
Löst grundlegende Gleichungstypen und Systeme (lineare Gleichungen, quadratische Gleichungen, trigonometrische Gleichungen und mehr).
Was unsere Kunden sagen
Häufig gestellte Fragen (FAQs)
Verschiedene Arten von mathematischen Gleichungen erfordern unterschiedliche Lösungsansätze:
Substitutionsmethode
– wird verwendet, um Gleichungssysteme mit zwei Variablen zu lösen;
Eliminationsmethode – dient
dazu, Variablen zu eliminieren und eine bestimmte Lösung zu finden;
Quadratische Ergänzung / Wurzelnformel
– geeignet zur Lösung quadratischer Gleichungen;
Graphische oder numerische Methoden – anwendbar
auf Gleichungen höheren Grades oder solche, die keine analytische Lösung haben;
Gleichungsrechner
– ideal, um strukturell komplexe oder zeitaufwendige Gleichungen schnell zu lösen, während er auch einen
detaillierten, schrittweisen Lösungsprozess bietet.
Die Methode des Quadratische Vervollständigens ist eine Technik zur Lösung quadratischer Gleichungen der
Form
𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0.
Dabei wird der Ausdruck in eine vollständige quadratische Form umgewandelt,
wie zum Beispiel
(𝑥 + 𝑑)² = 𝑒,
was die Gleichung visuell leichter lösbar macht. Diese Methode ist
besonders nützlich, wenn man quadratische Gleichungen löst, bei denen die Koeffizienten schwer mit den
Standardmethoden zu handhaben sind.
Die wichtigste Regel beim Lösen von Gleichungen online ist das Bewahren des Gleichgewichts zwischen der
linken und rechten Seite einer Gleichung.
Egal, welche Operation Sie auf einer Seite durchführen – sei
es Addition, Subtraktion, Multiplikation oder Division – Sie müssen dasselbe auf der anderen Seite tun.
Andernfalls wird das grundlegende Prinzip der Gleichung als Gleichheit verletzt, und das Ergebnis des Lösens
einer Gleichung wird falsch sein.
Die Schritte sind wie folgt:
1. Terme verschieben: Überführen Sie die Unbekannten auf eine Seite
der Gleichung und die Konstanten auf die andere Seite.
2. Vereinfachen: Fassen Sie ähnliche
Terme zusammen und vereinfachen Sie den Ausdruck.
3. Lösen: Verwenden Sie Addition, Subtraktion,
Multiplikation oder Division, um die Gleichung in die Form 𝑥 = Wert zu bringen. Achten Sie darauf, dass jede
Operation gleichzeitig auf beiden Seiten der Gleichung angewendet wird, wenn Sie Gleichungen online lösen.
Das Vereinfachen ist eine grundlegende Operation beim Lösen von Gleichungen und umfasst normalerweise:
1.
Entfernen von Klammern;
2. Entfernen von Klammern;
3. Befolgen der Rechenregeln (PEMDAS: Klammern
→ Exponenten → Multiplikation/Division → Addition/Subtraktion), um die mathematische Gleichung zu
vereinfachen und das Lösen von Gleichungen online zu erleichtern.
1. Vereinfache beide Seiten: Fasse ähnliche Terme zusammen und erweitere Klammern.
2. Isoliere die Variable: Bringe alle Terme, die die Variable enthalten, auf eine Seite. Move all terms containing the variable to
one side.
3. Bestimme den Wert der Variable: Verwende inverse Operationen, um die Koeffizienten
zu vereinfachen und das endgültige Ergebnis zu finden.
Geben Sie einfach eine mathematische Gleichung online ein. Dieser Gleichungsrechner erkennt automatisch die Variablen und die Struktur der Gleichung und verwendet intelligente Algorithmen (wie algebraische Transformationen, numerische Methoden und andere), um die Gleichung online zu lösen. Anschließend zeigt er schrittweise Lösungen mit Begründungen für jede Phase an. Dies ist ideal zum Lernen, Überprüfen von Mathematikhausaufgaben oder zur Verifikation komplexer Beispiele.
📘 Vollständige Liste der unterstützten mathematischen Funktionen
Erforschen Sie die Syntax und Notationen, die Sie im Decopy AI Gleichungsrechner verwenden können.
📂 Klicken Sie, um die unterstützten Funktionen anzuzeigen
| Funktion | Beschreibung |
|---|---|
| abs(x) | Absolute value of x |
| arccos(x) | Arkuskosinus von x |
| arccosh(x) | Hyperbolischer Arkuskosinus |
| arcsin(x) | Arkussinus von x |
| arcsinh(x) | Hyperbolischer Arkussinus |
| arctg(x) | Arkustangens von x |
| arctgh(x) | Hyperbolischer Arkustangens |
| asec(x) | Arkusekans von x |
| asech(x) | Hyperbolischer Arkusekans |
| cbrt(x) | Kubikwurzel von x |
| ceiling(x) | Runden auf die nächste ganze Zahl |
| chi(x) | Hyperbolischer Kosinusintegral |
| cos(x) | Kosinus von x |
| cosh(x) | Hyperbolischer Kosinus |
| cosec(x), csc(x) | Kosekans von x |
| ctg(x) | Kotangens von x |
| diracdelta(x) | Dirac-Delta-Funktion |
| e | Eulersche Zahl ≈ 2.71828 |
| exp(x) | Exponentialfunktion (e^x) |
| factorial(x), x! | Fakultät von x |
| floor(x) | Runden auf die nächste ganze Zahl |
| gamma(x) | Gamma-Funktion |
| heaviside(x) | Heaviside-Sprungfunktion |
| i | Imaginäre Einheit (√-1) |
| lambertw(x) | Lambert-W-Funktion |
| ln(x), log(x) | Natürlicher Logarithmus |
| log(a,x) | Logarithmus mit Basis a |
| oo | Unendlichkeit |
| pi | Pi ≈ 3.14159 |
| sec(x) | Sekans von x |
| sech(x) | Hyperbolischer Sekans |
| sign(x) | Zeichen einer Zahl |
| sin(x) | Sinus von x |
| sinh(x) | Hyperbolischer Sinus |
| sqrt(x) | Quadratwurzel |
| sqr(x), x^2 | Quadrat von x |
| Si(x), Ci(x), Shi(x), Chi(x) | Integrale trigonometrische und hyperbolische Funktionen |
| tg(x), tan(x) | Tangens |
| tgh(x) | Hyperbolischer Tangens |
| x + y, x - y | Addition, Subtraktion |
| x * y, x / y | Multiplikation, Division |
| x^n, pow(x,n) | Potenzierung |