Schüler
Erkunden Sie die Verbindung zwischen Algebra und Geometrie, vertiefen Sie das Verständnis mathematischer Konzepte und nutzen Sie den Geometrie-Rechner für Aufgaben und Projekte.
Der kostenlose Geometrie-Rechner kann geometrische Figuren zeichnen und deren Eigenschaften berechnen, wodurch eine effiziente Lösung für das Lernen und Erkunden von Geometrieproblemen bereitgestellt wird.
Der Geometrie-Rechner ist ein leistungsstarker Rechner für Geometrie, der Funktionen aus Algebra, Geometrie und Datenanalyse integriert. Er ist für das Lernen, Lehren und die Durchführung verschiedener Arten von geometrischer Forschung konzipiert. Der Online-Geometrie-Rechner hilft Nutzern, geometrische Probleme intuitiver und effizienter zu erkunden und zu berechnen.
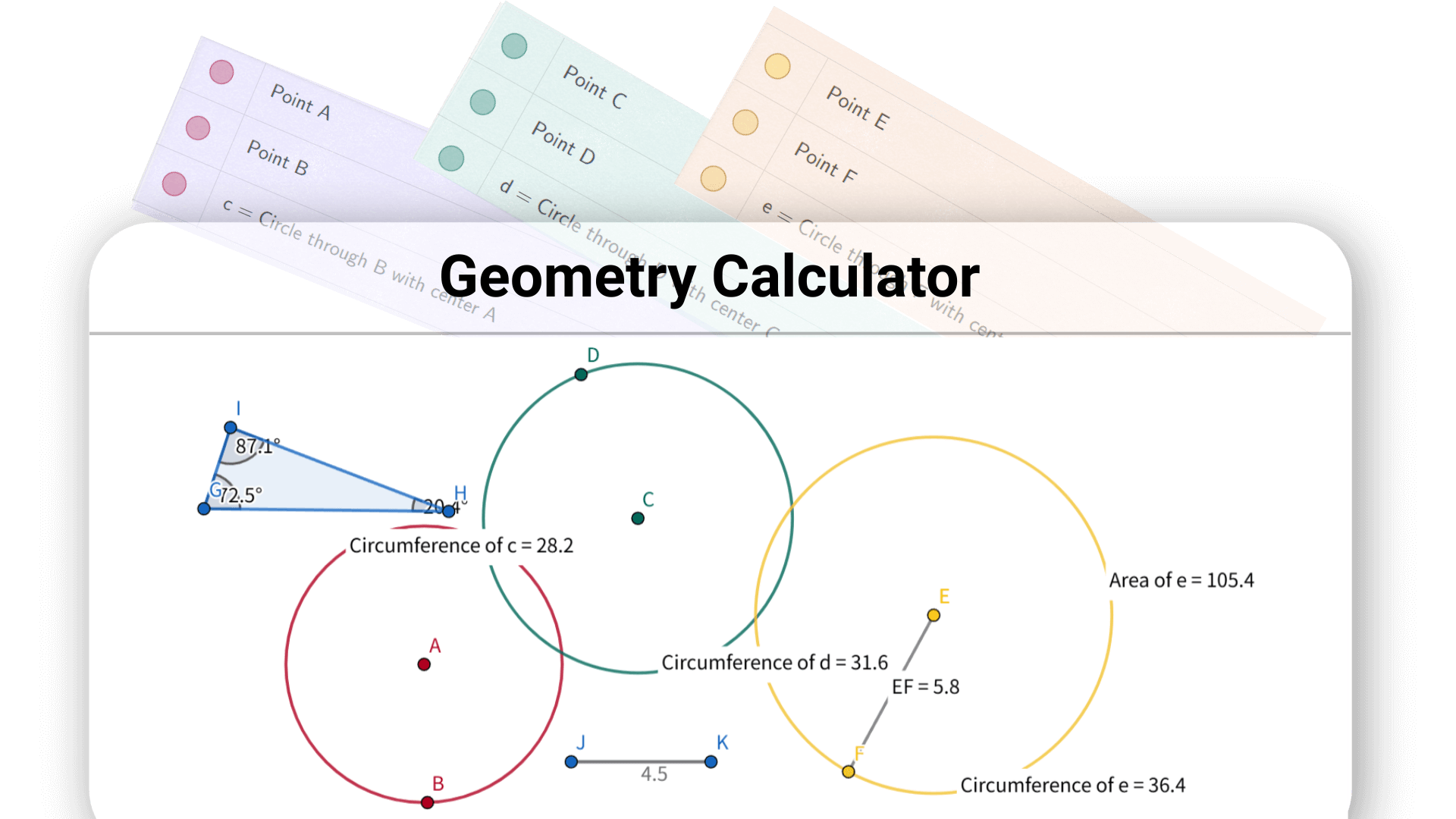
Decopys bester Geometrie-Rechner spart Ihnen wertvolle Zeit – kein Blättern mehr in Lehrbüchern oder Skizzieren auf Papier. Sie können sich auf das Verständnis geometrischer Konzepte konzentrieren, anstatt sich in komplexen Berechnungen zu verlieren.
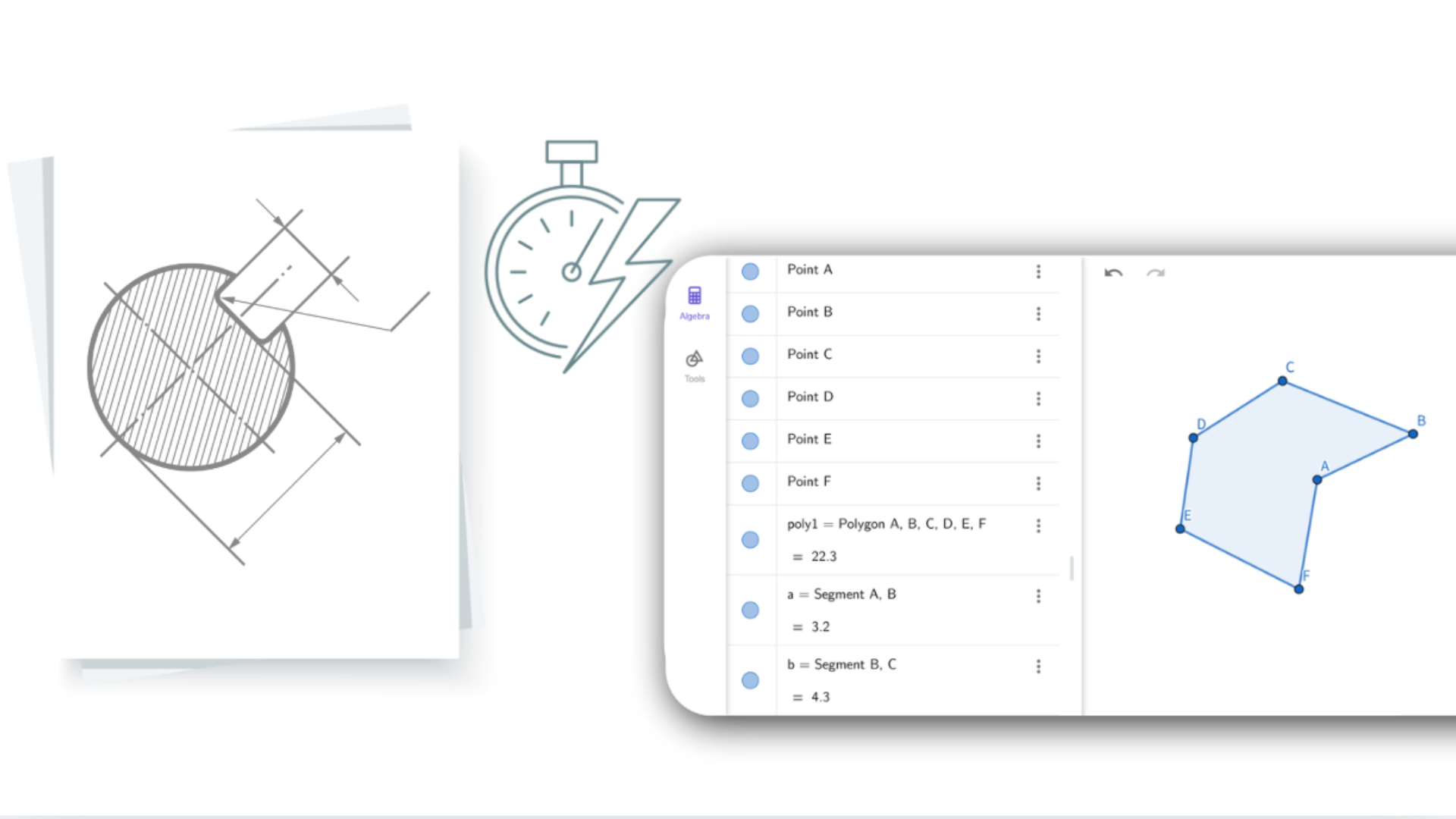
Durch die Eingabe von Gleichungen oder Koordinaten zeigt der Geometrie-Rechner sofort die entsprechenden Formen an. Das Anpassen einer Figur aktualisiert die zugehörigen algebraischen Ausdrücke in Echtzeit. Diese dynamische Interaktion verbindet Algebra mit Geometrie und hilft den Nutzern, Probleme aus verschiedenen Blickwinkeln zu verstehen. Abstrakte Mathematik wird durch den Geometrie-Rechner anschaulich und leichter verständlich.
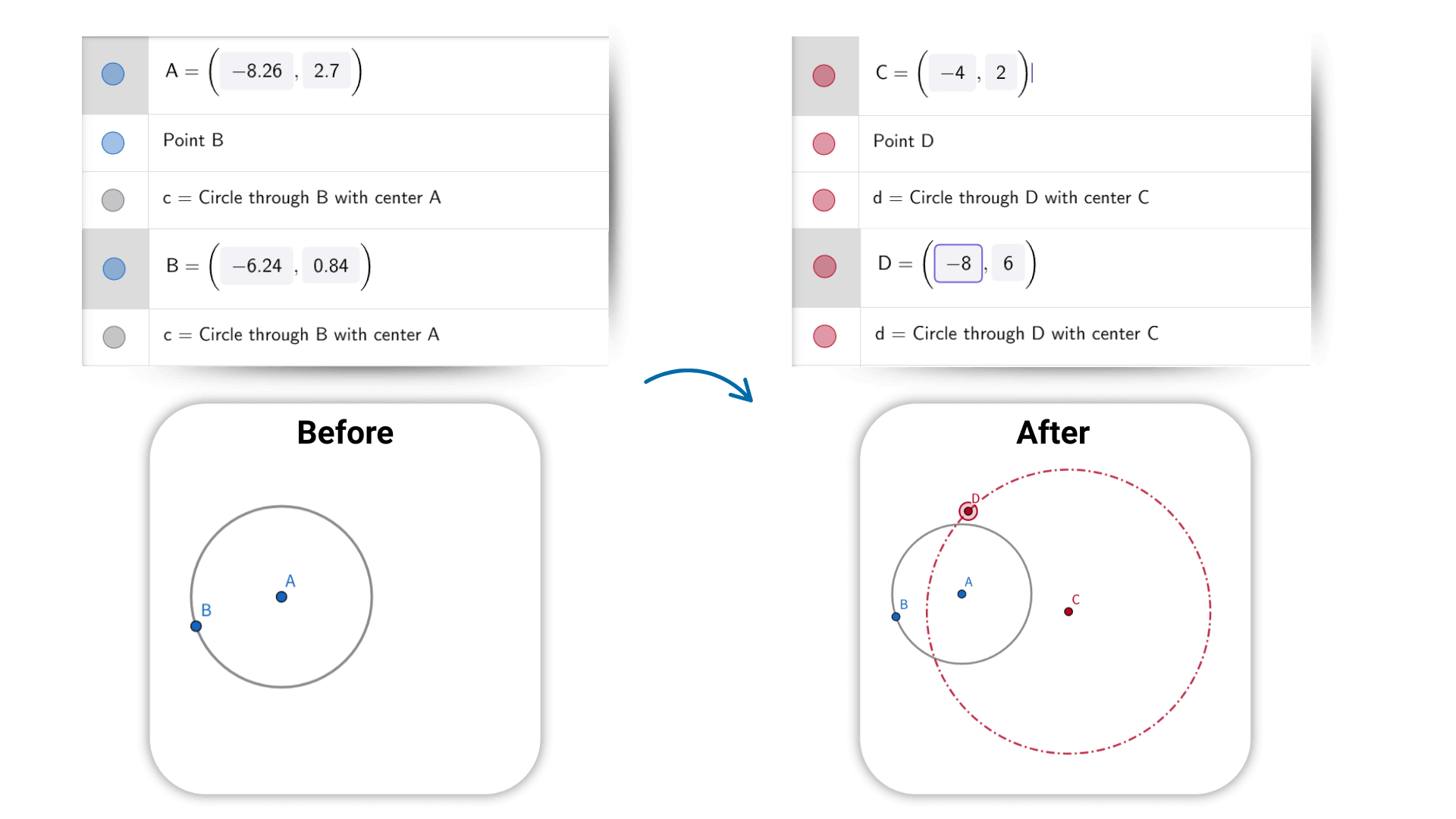
Der Geometrie-Rechner unterstützt Transformationen wie Verschiebung, Drehung und Skalierung. Mit einfachen Aktionen können Sie Formänderungen in Echtzeit sehen. Figuren, Ausdrücke und Daten sind vollständig interaktiv – das Ziehen eines Punktes oder das Anpassen eines Parameters aktualisiert automatisch die zugehörigen Beziehungen und Ergebnisse. Dieser Online-Geometrie-Rechner hilft Ihnen, zu erforschen, wie geometrische Objekte miteinander verbunden sind und sich verhalten, was das Verständnis ihrer dynamischen Natur erleichtert.
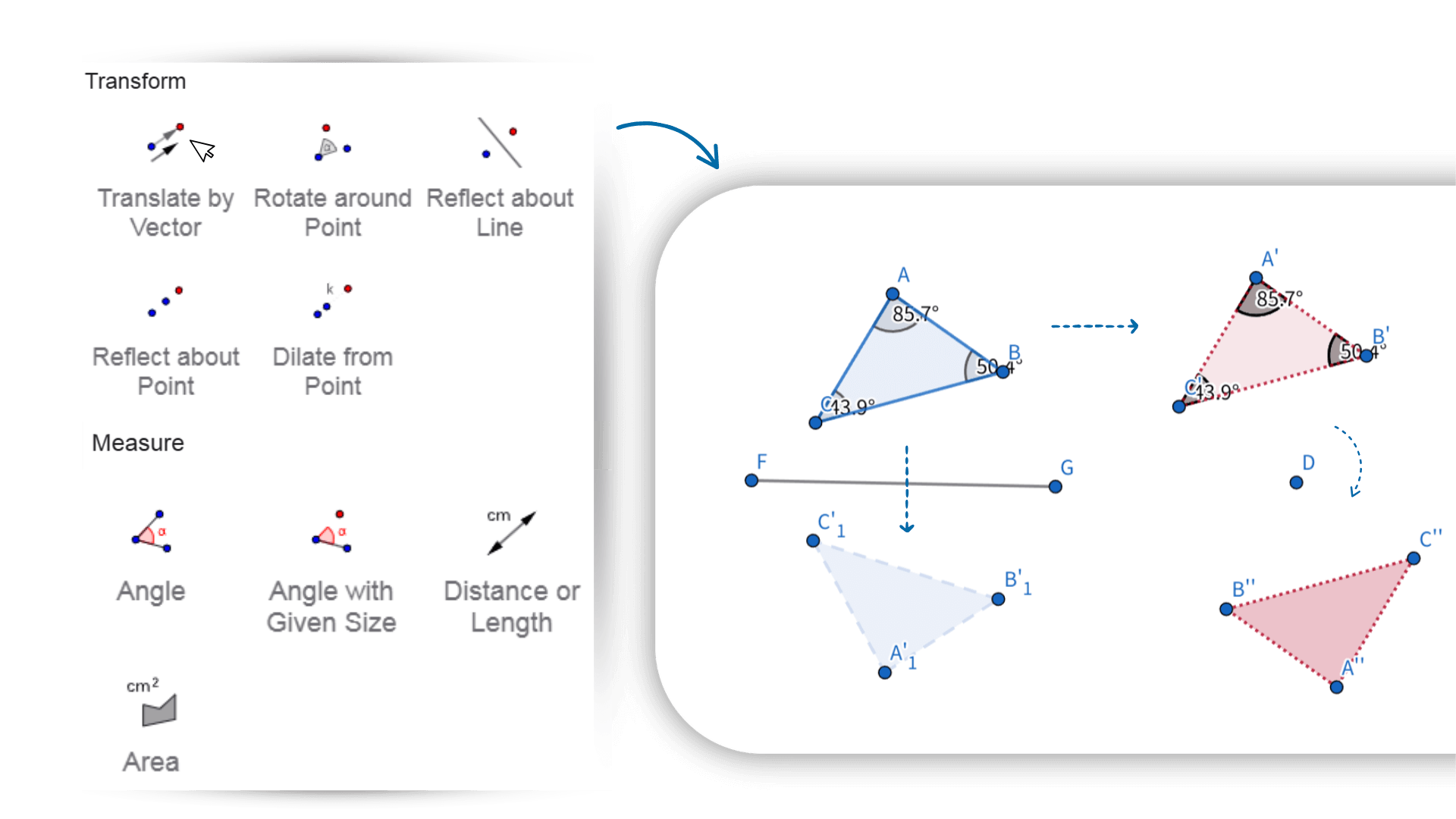
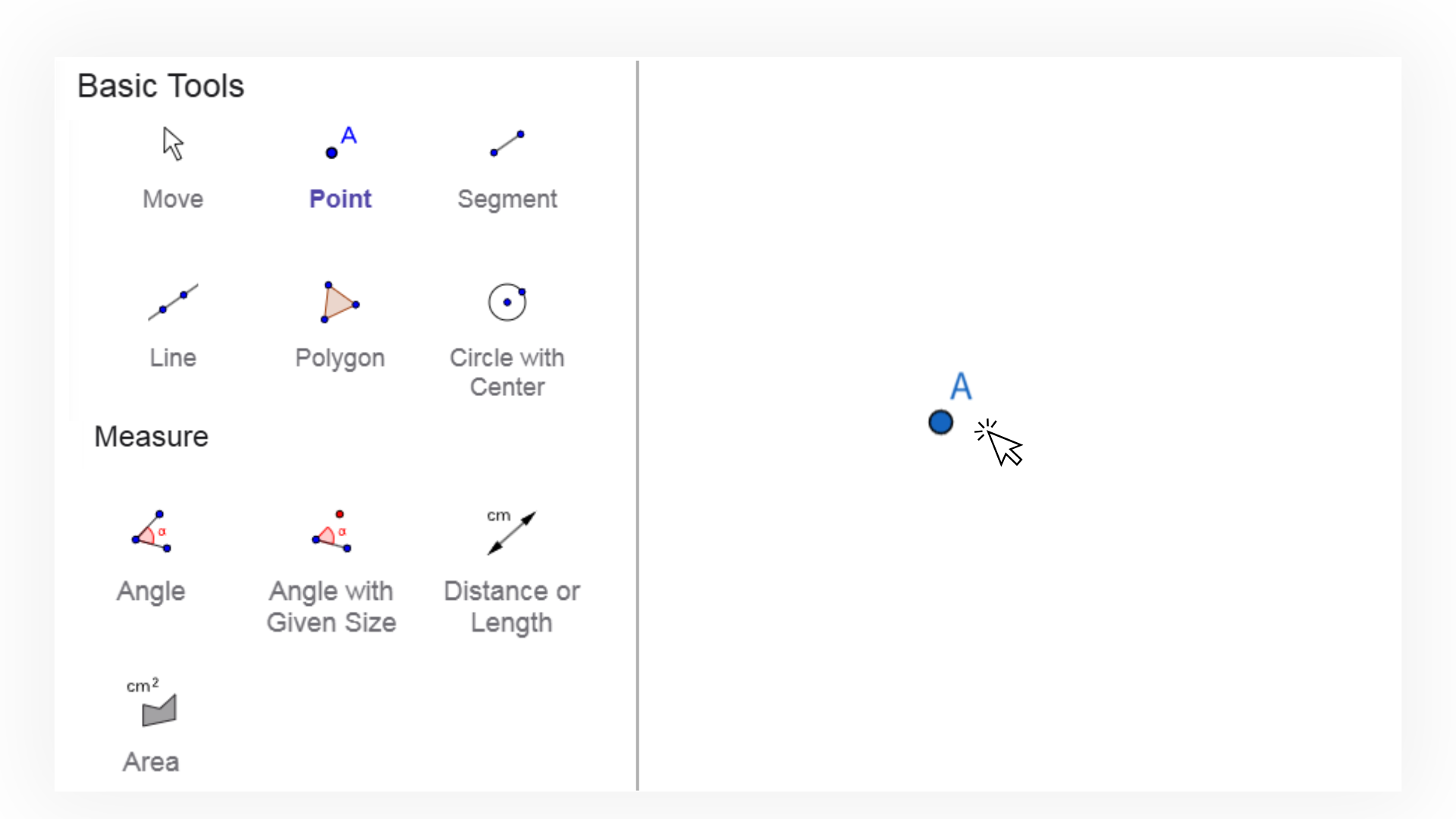
1. ![]() Wählen Sie das Geraden-Werkzeug aus und erstellen Sie eine
beliebige Gerade AB, indem Sie zweimal in die Grafikansicht
klicken.
Wählen Sie das Geraden-Werkzeug aus und erstellen Sie eine
beliebige Gerade AB, indem Sie zweimal in die Grafikansicht
klicken.
2. ![]() Erstellen Sie eine Gerade BC erneut mit dem
Geraden-Werkzeug.
Erstellen Sie eine Gerade BC erneut mit dem
Geraden-Werkzeug.
Tipp: Wählen Sie Punkt B und
klicken Sie dann in die Grafikansicht, um Punkt C zu
erstellen.
3. ![]() Aktivieren Sie das Parallelen-Werkzeug und erstellen Sie
eine Parallele zu AB durch Punkt C.
Aktivieren Sie das Parallelen-Werkzeug und erstellen Sie
eine Parallele zu AB durch Punkt C.
Tipp: Öffnen
Sie die Werkzeugkiste für spezielle Geraden, aktivieren Sie
das Parallelen-Werkzeug und wählen Sie zuerst die Gerade AB
und dann Punkt C.
4. ![]() Erstellen Sie erneut mit dem Parallelen-Werkzeug eine
Parallele zu BC durch Punkt A.
Erstellen Sie erneut mit dem Parallelen-Werkzeug eine
Parallele zu BC durch Punkt A.
5. ![]() Wählen Sie das Schnittpunkt-Werkzeug und erstellen Sie den
Schnittpunkt D der beiden Geraden.
Wählen Sie das Schnittpunkt-Werkzeug und erstellen Sie den
Schnittpunkt D der beiden Geraden.
Tipp: Öffnen
Sie die Werkzeugkiste für Punkte, aktivieren Sie das
Schnittpunkt-Werkzeug und klicken Sie direkt auf den
Schnittpunkt.
6. ![]() Aktivieren Sie das Polygon-Werkzeug und erstellen Sie das
Parallelogramm ABCD, indem Sie nacheinander alle Eckpunkte
auswählen.
Aktivieren Sie das Polygon-Werkzeug und erstellen Sie das
Parallelogramm ABCD, indem Sie nacheinander alle Eckpunkte
auswählen.
Hinweis: Um das Polygon zu schließen,
wählen Sie erneut den ersten Punkt.
7. ![]() Wählen Sie das Verschieben-Werkzeug und ziehen Sie die
Eckpunkte des Parallelogramms, um zu überprüfen, ob es
korrekt konstruiert wurde.
Wählen Sie das Verschieben-Werkzeug und ziehen Sie die
Eckpunkte des Parallelogramms, um zu überprüfen, ob es
korrekt konstruiert wurde.
1. ![]() Erstellen Sie die Strecke AB, indem Sie zweimal in die
Grafikansicht klicken.
Erstellen Sie die Strecke AB, indem Sie zweimal in die
Grafikansicht klicken.
2. ![]() Konstruiere einen Kreis mit Mittelpunkt B durch A, indem
Sie beide Punkte in dieser Reihenfolge auswählen.
Konstruiere einen Kreis mit Mittelpunkt B durch A, indem
Sie beide Punkte in dieser Reihenfolge auswählen.
3. ![]() Ziehen Sie die Punkte A und B, um zu überprüfen, ob der
Kreis mit ihnen verbunden ist.
Ziehen Sie die Punkte A und B, um zu überprüfen, ob der
Kreis mit ihnen verbunden ist.
4. ![]() Konstruiere einen Kreis mit Mittelpunkt B durch A, indem
Sie beide Punkte in dieser Reihenfolge auswählen.
Konstruiere einen Kreis mit Mittelpunkt B durch A, indem
Sie beide Punkte in dieser Reihenfolge auswählen.
5. ![]() Schneiden Sie beide Kreise, indem Sie sie auswählen, um
Punkt C zu erhalten.
Schneiden Sie beide Kreise, indem Sie sie auswählen, um
Punkt C zu erhalten.
6. ![]() Erstellen Sie das Polygon ABC gegen den Uhrzeigersinn. Um
das Polygon zu schließen, wählen Sie erneut den ersten
Punkt.
Erstellen Sie das Polygon ABC gegen den Uhrzeigersinn. Um
das Polygon zu schließen, wählen Sie erneut den ersten
Punkt.
7. ![]() Blenden Sie die beiden Kreise aus, indem Sie das Objekt
ein-/ausblenden-Werkzeug aktivieren und sie auswählen.
Bestätigen Sie Ihre Auswahl, indem Sie das
Verschieben-Werkzeug wählen.
Blenden Sie die beiden Kreise aus, indem Sie das Objekt
ein-/ausblenden-Werkzeug aktivieren und sie auswählen.
Bestätigen Sie Ihre Auswahl, indem Sie das
Verschieben-Werkzeug wählen.
8. ![]() Zeigen Sie die Innenwinkel des Dreiecks an, indem Sie in
das Dreieck klicken.
Zeigen Sie die Innenwinkel des Dreiecks an, indem Sie in
das Dreieck klicken.
Tipp: Wenn Sie die Außenwinkel Ihres Dreiecks
erhalten, haben Sie das Polygon wahrscheinlich im
Uhrzeigersinn erstellt.
9. ![]() Führen Sie den Zieh-Test durch, um zu überprüfen, ob die
Konstruktion korrekt ist.
Führen Sie den Zieh-Test durch, um zu überprüfen, ob die
Konstruktion korrekt ist.
1. ![]() Erstellen Sie ein beliebiges Dreieck ABC, indem Sie dreimal
in die Grafikansicht klicken und dann erneut den zuerst
erstellten Punkt auswählen.
Erstellen Sie ein beliebiges Dreieck ABC, indem Sie dreimal
in die Grafikansicht klicken und dann erneut den zuerst
erstellten Punkt auswählen.
2. ![]() Konstruiere die Mittelsenkrechte für jede Seite des
Dreiecks.
Konstruiere die Mittelsenkrechte für jede Seite des
Dreiecks.
Tipp: Das Mittelsenkrechten-Werkzeug
kann auf ein vorhandenes Segment angewendet werden.
3. ![]() Erstellen Sie den Schnittpunkt D von zwei der
Mittelsenkrechten.
Erstellen Sie den Schnittpunkt D von zwei der
Mittelsenkrechten.
Tipp: Das
Schnittpunkt-Werkzeug kann auf den Schnittpunkt von drei
Geraden oder durch sukzessive Auswahl von zwei der drei
Mittelsenkrechten angewendet werden.
4. ![]() Konstruiere einen Kreis mit Mittelpunkt D durch einen der
Eckpunkte des Dreiecks ABC, indem Sie zuerst D und dann
einen der Eckpunkte auswählen.
Konstruiere einen Kreis mit Mittelpunkt D durch einen der
Eckpunkte des Dreiecks ABC, indem Sie zuerst D und dann
einen der Eckpunkte auswählen.
5. ![]() Führen Sie den Zieh-Test durch, indem Sie die Eckpunkte des
Dreiecks verschieben, um zu überprüfen, ob Ihre Konstruktion
korrekt ist.
Führen Sie den Zieh-Test durch, indem Sie die Eckpunkte des
Dreiecks verschieben, um zu überprüfen, ob Ihre Konstruktion
korrekt ist.
1. ![]() Stellen Sie sicher, dass Sie das Bild der gelben Blume auf
Ihrem Computer gespeichert haben, bevor Sie mit der
eigentlichen Konstruktion beginnen.
Stellen Sie sicher, dass Sie das Bild der gelben Blume auf
Ihrem Computer gespeichert haben, bevor Sie mit der
eigentlichen Konstruktion beginnen.
2. ![]() Erstellen Sie einen neuen Punkt A.
Erstellen Sie einen neuen Punkt A.
3. ![]() Konstruiere eine Spiegelachse durch zwei neue Punkte, indem
Sie zweimal in die Grafikansicht klicken.
Konstruiere eine Spiegelachse durch zwei neue Punkte, indem
Sie zweimal in die Grafikansicht klicken.
4. ![]() Spiegeln Sie Punkt A an der Geraden, um sein Bild A’ zu
erhalten.
Spiegeln Sie Punkt A an der Geraden, um sein Bild A’ zu
erhalten.
Tipp: Wählen Sie zuerst Punkt A und
dann die Gerade.
5. ![]() Erstellen Sie eine Strecke zwischen Punkt A und seinem Bild
A’, indem Sie beide Punkte auswählen.
Erstellen Sie eine Strecke zwischen Punkt A und seinem Bild
A’, indem Sie beide Punkte auswählen.
6. ![]() Aktivieren Sie die Spur für die Punkte A und A′.
Aktivieren Sie die Spur für die Punkte A und A′.
Tipp:
Rechtsklick (MacOS: Ctrl-Klick) auf einen Punkt und wählen
Sie Spur anzeigen.
Hinweis: Immer wenn Punkt A
bewegt wird, hinterlässt er eine Spur in der
Grafikansicht.
7. ![]() Ziehen Sie Punkt A, um eine Spur zu zeichnen.
Ziehen Sie Punkt A, um eine Spur zu zeichnen.
Tipp:
Der Menüpunkt Ansichten aktualisieren im Ansichtsmenü löscht
alle Spuren.
1. ![]() Stellen Sie sicher, dass Sie das Bild des Sonnenuntergangs
auf Ihrem Computer gespeichert haben, bevor Sie mit der
eigentlichen Konstruktion beginnen.
Stellen Sie sicher, dass Sie das Bild des Sonnenuntergangs
auf Ihrem Computer gespeichert haben, bevor Sie mit der
eigentlichen Konstruktion beginnen.
2. ![]() Fügen Sie das Bild des Sonnenuntergangs im linken Teil der
Grafikansicht mit dem Bild-Werkzeug ein.
Fügen Sie das Bild des Sonnenuntergangs im linken Teil der
Grafikansicht mit dem Bild-Werkzeug ein.
Hinweis:
Der erste Eckpunkt A und der zweite Eckpunkt B des Bildes
werden automatisch erstellt.
3. ![]() Verschieben Sie Punkt A in die linke untere Ecke des Bildes
und beobachten Sie, wie sich das Bild verändert.
Verschieben Sie Punkt A in die linke untere Ecke des Bildes
und beobachten Sie, wie sich das Bild verändert.
4. ![]() Löschen Sie Punkt B mit dem Löschen-Werkzeug.
Löschen Sie Punkt B mit dem Löschen-Werkzeug.
5. ![]() Erstellen Sie einen neuen Punkt B, indem Sie B = A + (3, 0)
in die Eingabezeile eingeben.
Erstellen Sie einen neuen Punkt B, indem Sie B = A + (3, 0)
in die Eingabezeile eingeben.
Tipp: Vergessen
Sie nicht, nach der Eingabe die Eingabetaste zu
drücken.
6. ![]() Setzen Sie den neuen Punkt B als ZWEITEN Eckpunkt des
Bildes, um die Breite auf 3 cm zu ändern.
Setzen Sie den neuen Punkt B als ZWEITEN Eckpunkt des
Bildes, um die Breite auf 3 cm zu ändern.
Tipp:
Öffnen Sie die Einstellungen des Bildes und wählen Sie den
Reiter Position.
7. ![]() Erstellen Sie mit dem Geraden-Werkzeug eine vertikale
Gerade durch zwei Punkte in der Mitte der
Grafikansicht.
Erstellen Sie mit dem Geraden-Werkzeug eine vertikale
Gerade durch zwei Punkte in der Mitte der
Grafikansicht.
8. ![]() Spiegeln Sie das Bild an der Geraden mit dem Werkzeug
Spiegelung an Gerade, indem Sie zuerst das Bild und dann die
Gerade auswählen.
Spiegeln Sie das Bild an der Geraden mit dem Werkzeug
Spiegelung an Gerade, indem Sie zuerst das Bild und dann die
Gerade auswählen.
9. ![]() Sie können die Transparenz des Bildes verringern, um es
besser vom Original zu unterscheiden (Einstellungen des
Bildes, Reiter Farbe).
Sie können die Transparenz des Bildes verringern, um es
besser vom Original zu unterscheiden (Einstellungen des
Bildes, Reiter Farbe).
1. ![]() Stellen Sie sicher, dass Sie das Bild von Bart Simpson auf
Ihrem Computer gespeichert haben, bevor Sie mit der
eigentlichen Konstruktion beginnen.
Stellen Sie sicher, dass Sie das Bild von Bart Simpson auf
Ihrem Computer gespeichert haben, bevor Sie mit der
eigentlichen Konstruktion beginnen.
2. ![]() Wählen Sie das Bild-Werkzeug, um das Bild von Bart
einzufügen.
Wählen Sie das Bild-Werkzeug, um das Bild von Bart
einzufügen.
Tipp: Der Geometrie-Rechner erstellt
automatisch den ersten und zweiten Eckpunkt A und B des
Bildes.
3. ![]() Ziehen Sie den ersten Eckpunkt A des Bildes auf die
Position (1, 1).
Ziehen Sie den ersten Eckpunkt A des Bildes auf die
Position (1, 1).
4. ![]() Erstellen Sie den Punkt D = (1, 3.9).
Erstellen Sie den Punkt D = (1, 3.9).
Tipp: Sie
können die Koordinaten direkt in die Eingabezeile
eingeben.
5. ![]() Setzen Sie Punkt D als VIERTEN Eckpunkt des Bildes.
Setzen Sie Punkt D als VIERTEN Eckpunkt des Bildes.
Tipp:
Öffnen Sie die Einstellungen des Bildes und wählen Sie den
Reiter Position.
6. ![]() Erstellen Sie ein starres Dreieck ABD mit dem Werkzeug
Starres Polygon.
Erstellen Sie ein starres Dreieck ABD mit dem Werkzeug
Starres Polygon.
Tipp: Schließen Sie das
Polygon, indem Sie erneut den ersten Punkt auswählen. Das
resultierende Polygon behält seine Form beim Verschieben. Es
kann durch Ziehen von zwei Eckpunkten verschoben oder
rotiert werden.
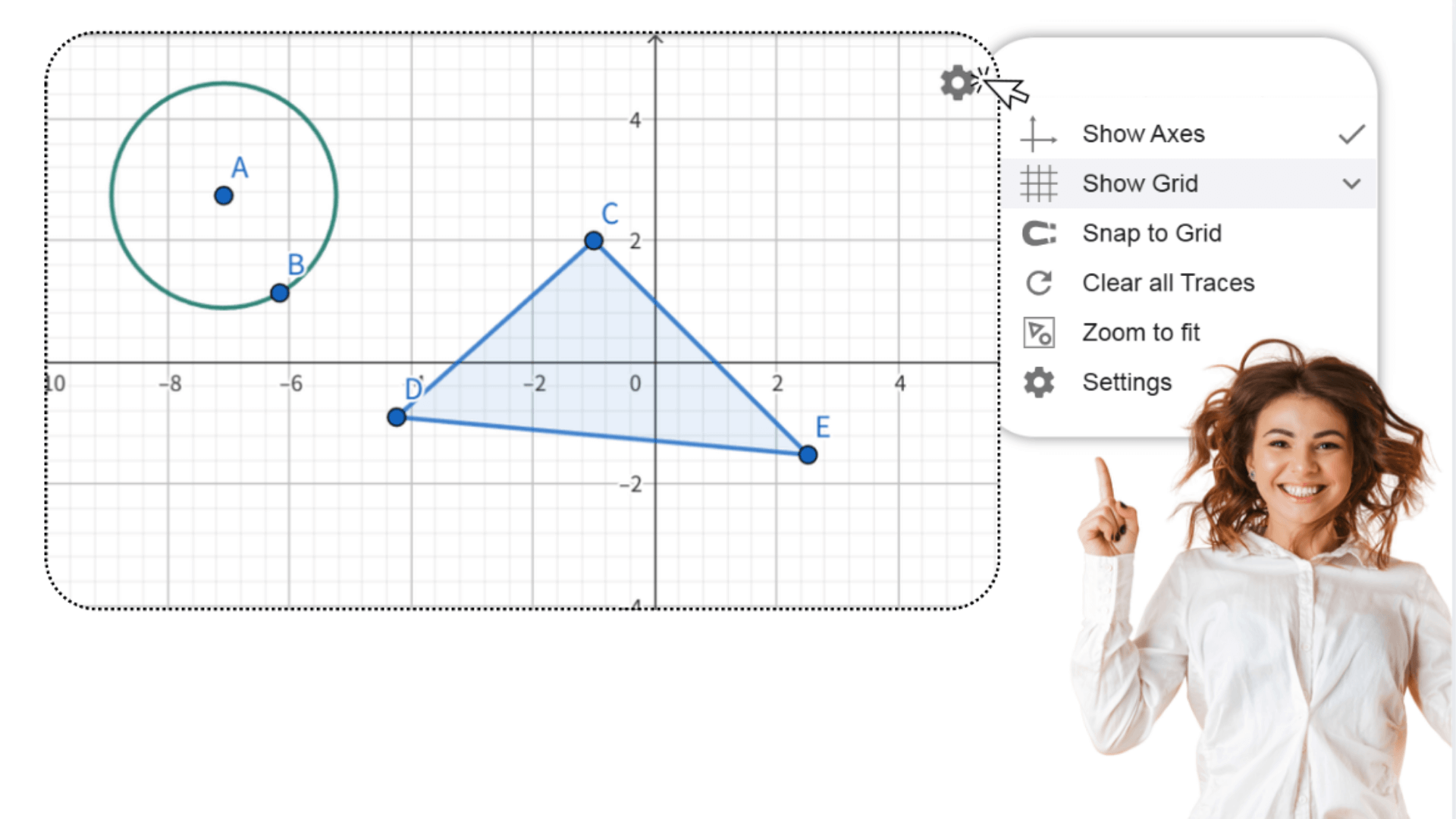
1. ![]() Erstellen Sie ein beliebiges Dreieck ABC im ersten
Quadranten, indem Sie die Eckpunkte auf Gitterpunkten
platzieren.
Erstellen Sie ein beliebiges Dreieck ABC im ersten
Quadranten, indem Sie die Eckpunkte auf Gitterpunkten
platzieren.
2. ![]() Erstellen Sie einen neuen Punkt D am Ursprung des
Koordinatensystems.
Erstellen Sie einen neuen Punkt D am Ursprung des
Koordinatensystems.
3. ![]() Benenne den Punkt D in O um.
Benenne den Punkt D in O um.
Tipp: Wählen Sie
Punkt D und tippen Sie einfach O, um den Umbenennen-Dialog
zu öffnen.
4. ![]() Erstellen Sie einen Schieberegler für den Winkel α.
Erstellen Sie einen Schieberegler für den Winkel α.
Tipp:
Im Schieberegler-Dialogfenster aktivieren Sie Winkel und
setzen das Inkrement auf 90°. Achten Sie darauf, das
°-Symbol nicht zu löschen.
5. ![]() Verwenden Sie das Drehen-um-Punkt-Werkzeug, um das Dreieck
ABC um Punkt O um den Winkel α zu drehen.
Verwenden Sie das Drehen-um-Punkt-Werkzeug, um das Dreieck
ABC um Punkt O um den Winkel α zu drehen.
Tipps:
Aktivieren Sie das Werkzeug und wählen Sie das Dreieck,
bevor Sie das Rotationszentrum auswählen. Im erscheinenden
Dialog geben Sie α als Winkel über die virtuelle Tastatur
ein und wählen Sie die Drehung gegen den
Uhrzeigersinn.
6. ![]() Erstellen Sie die Strecken AO und A’O.
Erstellen Sie die Strecken AO und A’O.
7. ![]() Erstellen Sie den Winkel AOA’.
Erstellen Sie den Winkel AOA’.
Tipp: Wählen Sie
die Punkte gegen den Uhrzeigersinn aus.
8. ![]() Blenden Sie die Beschriftung des Winkels AOA’ aus.
Blenden Sie die Beschriftung des Winkels AOA’ aus.
9. ![]() Bewegen Sie den Schieberegler und erkunden Sie das Bild des
Dreiecks.
Bewegen Sie den Schieberegler und erkunden Sie das Bild des
Dreiecks.
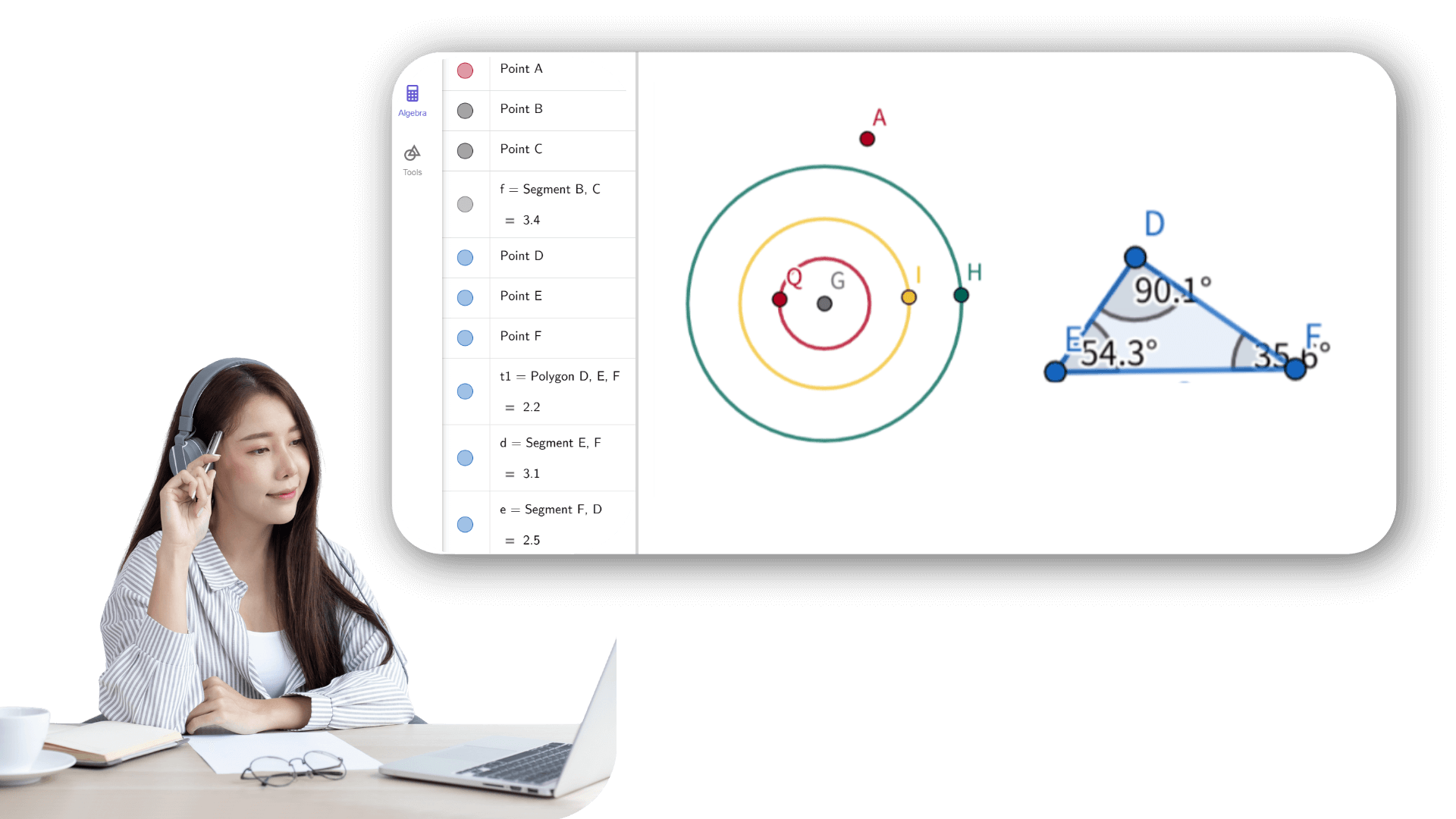
1. ![]() Erstellen Sie Schieberegler a, b und c für die Seitenlängen
des Dreiecks mit einem Intervall von 0 bis 10 und einer
Schrittweite von jeweils 0,5.
Erstellen Sie Schieberegler a, b und c für die Seitenlängen
des Dreiecks mit einem Intervall von 0 bis 10 und einer
Schrittweite von jeweils 0,5.
2. ![]() Setzen Sie die Werte der Schieberegler auf a = 8, b = 6,5
und c = 10.
Setzen Sie die Werte der Schieberegler auf a = 8, b = 6,5
und c = 10.
3. ![]() Erstellen Sie die Strecke f mit der vorgegebenen Länge
c.
Erstellen Sie die Strecke f mit der vorgegebenen Länge
c.
Tipp: Die Punkte A und B sind die Endpunkte
der Strecke.
4. ![]() Erstellen Sie einen Kreis d mit Mittelpunkt A und Radius
b.
Erstellen Sie einen Kreis d mit Mittelpunkt A und Radius
b.
5. ![]() Erstellen Sie einen Kreis e mit Mittelpunkt B und Radius
a.
Erstellen Sie einen Kreis e mit Mittelpunkt B und Radius
a.
6. ![]() Konstruiere den Schnittpunkt C der beiden Kreise e und
f.
Konstruiere den Schnittpunkt C der beiden Kreise e und
f.
7. ![]() Erstellen Sie das Dreieck ABC.
Erstellen Sie das Dreieck ABC.
8. ![]() Erstellen Sie die Innenwinkel α, β und γ des Dreiecks
ABC.
Erstellen Sie die Innenwinkel α, β und γ des Dreiecks
ABC.
9. ![]() Erstellen Sie einen Punkt D auf Kreis d.
Erstellen Sie einen Punkt D auf Kreis d.
10. ![]() Erstellen Sie die Strecke g zwischen den Punkten A und
D.
Erstellen Sie die Strecke g zwischen den Punkten A und
D.
11. ![]() Konstruiere den Mittelpunkt E der Strecke g.
Konstruiere den Mittelpunkt E der Strecke g.
12. ![]() Geben Sie Text1: b ein und heften Sie ihn an Punkt E an.
Geben Sie Text1: b ein und heften Sie ihn an Punkt E an.
Tipp:
Nach Auswahl des Text-Werkzeugs klicken Sie auf Punkt E.
Öffnen Sie Erweitert und wählen Sie b im Reiter
Objekte.
13. ![]() Erstellen Sie einen Punkt F auf Kreis e.
Erstellen Sie einen Punkt F auf Kreis e.
14. ![]() Erstellen Sie die Strecke h zwischen den Punkten B und
F.
Erstellen Sie die Strecke h zwischen den Punkten B und
F.
15. ![]() Konstruiere den Mittelpunkt G der Strecke h.
Konstruiere den Mittelpunkt G der Strecke h.
16. ![]() Geben Sie Text2: a ein und heften Sie ihn an Punkt G
an.
Geben Sie Text2: a ein und heften Sie ihn an Punkt G
an.
17. ![]() Blenden Sie die Punkte D, E, F und G mit dem Objekt
ein-/ausblenden-Werkzeug aus.
Blenden Sie die Punkte D, E, F und G mit dem Objekt
ein-/ausblenden-Werkzeug aus.
18. ![]() Verbessern Sie Ihre Konstruktion mit der Style Bar und
gleichen Sie die Farben entsprechender Objekte an.
Verbessern Sie Ihre Konstruktion mit der Style Bar und
gleichen Sie die Farben entsprechender Objekte an.
1. ![]() Erstellen Sie ein Dreieck ABC mit gegen den Uhrzeigersinn
verlaufender Orientierung.
Erstellen Sie ein Dreieck ABC mit gegen den Uhrzeigersinn
verlaufender Orientierung.
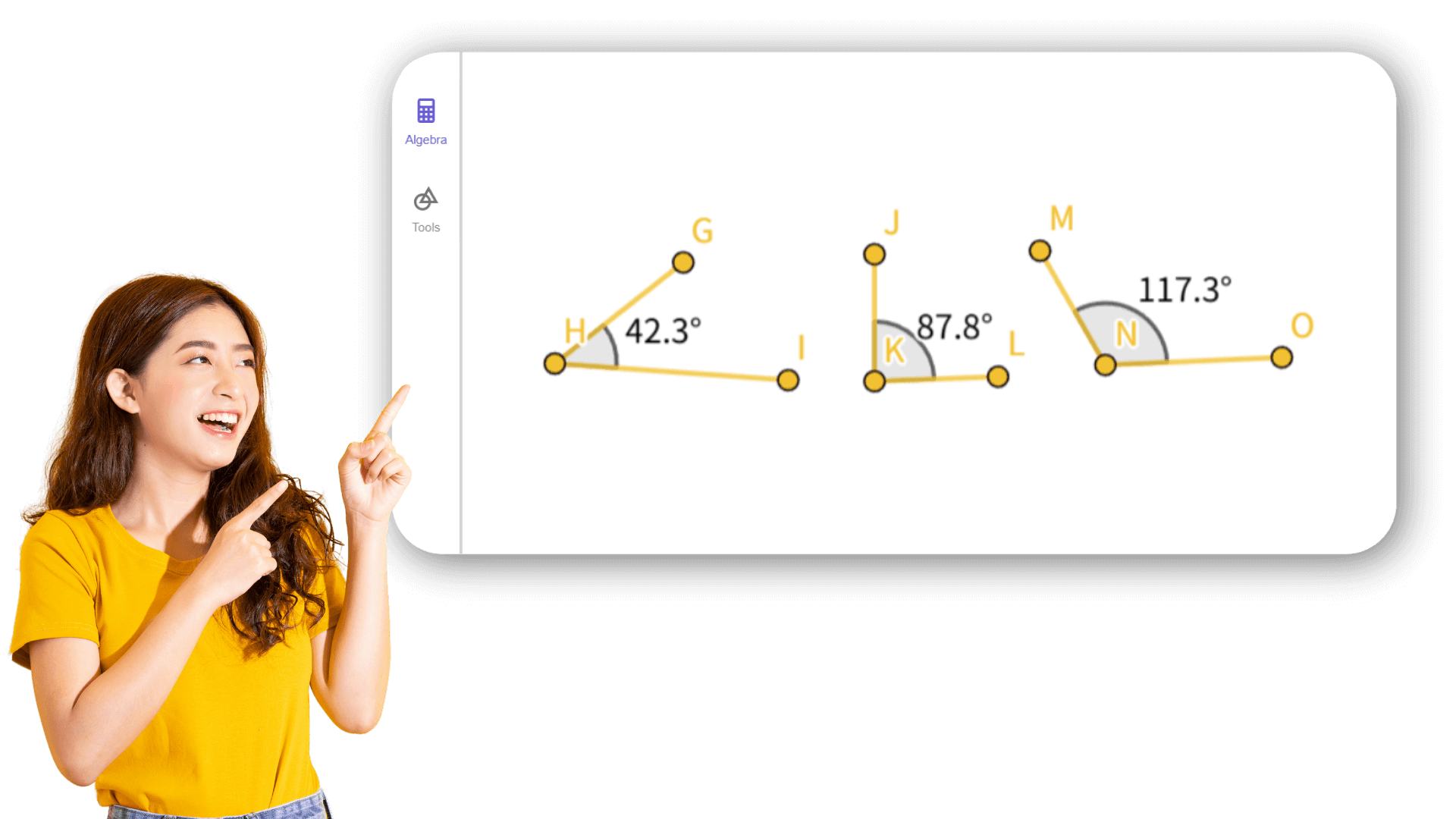
2. ![]() Erstellen Sie die Winkel α, β und γ des Dreiecks ABC.
Erstellen Sie die Winkel α, β und γ des Dreiecks ABC.
3. ![]() Erstellen Sie einen Schieberegler für den Winkel δ mit
Intervall 0° bis 180° und Schrittweite 10°.
Erstellen Sie einen Schieberegler für den Winkel δ mit
Intervall 0° bis 180° und Schrittweite 10°.
4. ![]() Erstellen Sie einen Schieberegler für den Winkel ε mit
Intervall 0° bis 180° und Schrittweite 10°.
Erstellen Sie einen Schieberegler für den Winkel ε mit
Intervall 0° bis 180° und Schrittweite 10°.
5. ![]() Erstellen Sie den Mittelpunkt D der Strecke AC und den
Mittelpunkt E der Strecke AB.
Erstellen Sie den Mittelpunkt D der Strecke AC und den
Mittelpunkt E der Strecke AB.
6. ![]() Drehen Sie das Dreieck um Punkt D um den Winkel δ
(Einstellung: im Uhrzeigersinn).
Drehen Sie das Dreieck um Punkt D um den Winkel δ
(Einstellung: im Uhrzeigersinn).
Tipp: Geben Sie
δ mit der virtuellen Tastatur ein.
7. ![]() Drehen Sie das Dreieck um Punkt E um den Winkel ε
(Einstellung: gegen den Uhrzeigersinn).
Drehen Sie das Dreieck um Punkt E um den Winkel ε
(Einstellung: gegen den Uhrzeigersinn).
Tipp:
Geben Sie ε mit der virtuellen Tastatur ein.
8. ![]() Bewegen Sie beide Schieberegler δ und ε, sodass 180°
angezeigt wird.
Bewegen Sie beide Schieberegler δ und ε, sodass 180°
angezeigt wird.
9. ![]() Erstellen Sie den Winkel ζ mit den Punkten A’C’B’.
Erstellen Sie den Winkel ζ mit den Punkten A’C’B’.
Tipp:
Um sicherzugehen, dass Sie die richtigen Eckpunkte
auswählen, ändern Sie den Winkel δ oder verwenden Sie
stattdessen den Befehl angle(A’, C’, B’).
10. ![]() Erstellen Sie den Winkel η mit den Punkten C'1B'1A'1.
Erstellen Sie den Winkel η mit den Punkten C'1B'1A'1.
Tipp:
Um sicherzugehen, dass Sie die richtigen Eckpunkte
auswählen, ändern Sie vorher den Winkel ε oder verwenden Sie
stattdessen den Befehl
angle(C'1, B'1, A'1).
11. ![]() Verbessern Sie Ihre Konstruktion mit der Style Bar.
Verbessern Sie Ihre Konstruktion mit der Style Bar.
Tipp:
Kongruente Winkel sollten die gleiche Farbe haben.
12. ![]() Erstellen Sie dynamischen Text, der die Innenwinkel und
deren Werte anzeigt (z. B. geben Sie α = ein und wählen Sie
α aus der Liste der Objekte im Reiter Erweitert).
Erstellen Sie dynamischen Text, der die Innenwinkel und
deren Werte anzeigt (z. B. geben Sie α = ein und wählen Sie
α aus der Liste der Objekte im Reiter Erweitert).
13. ![]() Berechnen Sie die Winkelsumme, indem Sie
Berechnen Sie die Winkelsumme, indem Sie
sum = α + β + γ in die Eingabezeile
eingeben.
14. ![]() Fügen Sie die Winkelsumme als dynamischen Text ein:
Fügen Sie die Winkelsumme als dynamischen Text ein:
α + β + γ = und wählen Sie sum aus der Liste
der Objekte im Reiter.
15. ![]() Gleichen Sie die Farben der entsprechenden Winkel und Texte
mit der Style Bar ab.
Gleichen Sie die Farben der entsprechenden Winkel und Texte
mit der Style Bar ab.
16. ![]() Fixieren Sie alle Texte, die nicht verschoben werden
sollen, mit der Style Bar.
Fixieren Sie alle Texte, die nicht verschoben werden
sollen, mit der Style Bar.
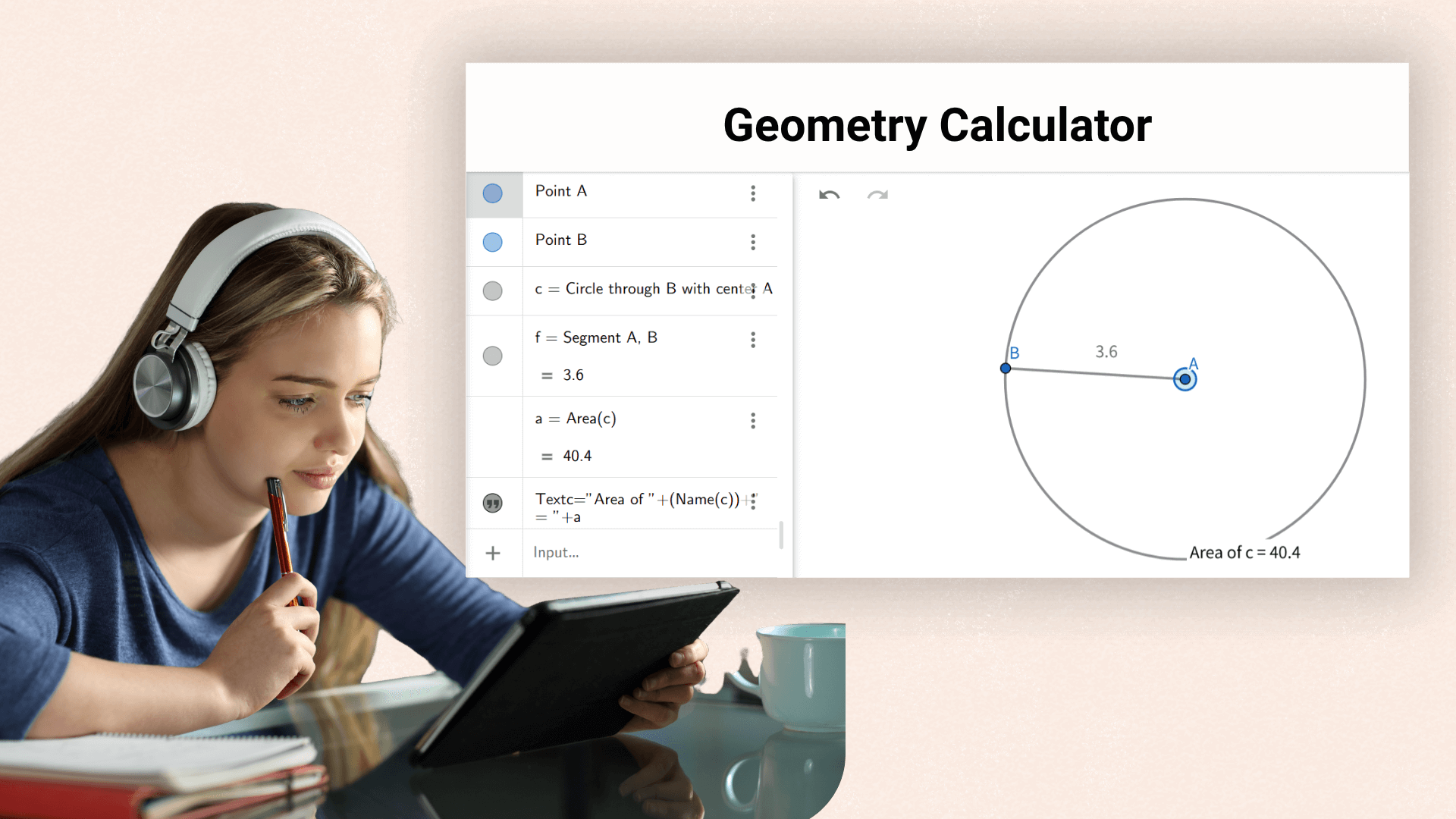
Hilft Schülern, Formeln schnell zu überprüfen und Aufgaben im Geometrieunterricht zu lösen, wodurch die Lerneffizienz gesteigert wird.
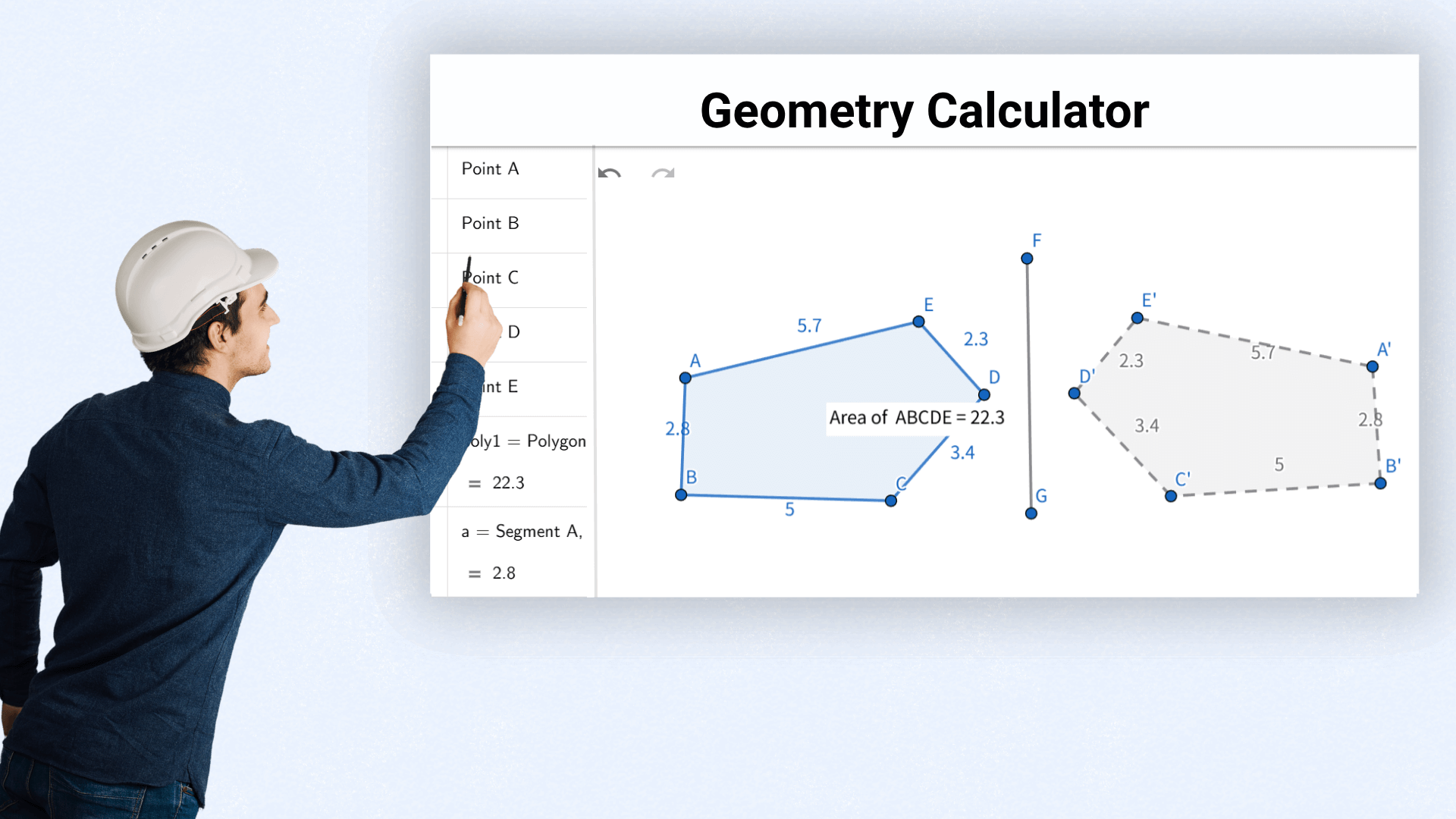
Architekten berechnen Flächen und Volumen, um die Machbarkeit von Entwürfen zu beurteilen und die räumliche Anordnung zu optimieren.

Hobbybastler nutzen den Geometrie-Rechner, um Materialien beim Erstellen geometrischer Bastelprojekte präzise zu vermessen.
Erkunden Sie die Verbindung zwischen Algebra und Geometrie, vertiefen Sie das Verständnis mathematischer Konzepte und nutzen Sie den Geometrie-Rechner für Aufgaben und Projekte.
Lehrkräfte nutzen den Geometrie-Rechner, um geometrische Konzepte im Unterricht anschaulich zu präsentieren und so die Unterrichtsqualität zu verbessern.
Ingenieure verlassen sich auf den Geometrie-Rechner, um Winkel und Längen in Bau- oder Maschinenkonstruktionen präzise zu berechnen und Fehler durch manuelle Berechnungen zu reduzieren.

Hobbybastler nutzen den Rechner, um beim Erstellen geometriebasierter Bastelarbeiten präzise Maße zu gewährleisten.
Nutzen Sie den Geometrie-Rechner, um schnell erste Entwurfsideen zu skizzieren und anzupassen und ein klares Verständnis räumlicher Beziehungen zu gewinnen, bevor Sie zu detaillierten CAD-Tools wechseln.

Forscher visualisieren komplexe Strukturen und analysieren Daten mit den Zeichen- und Rechenfunktionen des Rechners und unterstützen so die wissenschaftliche Arbeit.
Verwendet fortschrittliche Algorithmen, um hochpräzise geometrische Ergebnisse zu gewährleisten.
Einfache, intuitive Benutzeroberfläche mit klarem Arbeitsablauf – keine komplizierte Schulung erforderlich, auch nicht für neue Nutzer.
Vereint mehrere Werkzeuge und Funktionen, um verschiedenste Anforderungen an geometrische Berechnungen an einem Ort zu erfüllen.
Schnelle Leistung und reibungsloser Betrieb, auch bei großen Dateneingaben oder komplexen Formeln.
Formen präzise zeichnen und Größe sowie Eigenschaften steuern – eine verlässliche visuelle Grundlage für Analyse und Forschung.
Alle Funktionen des Online-Geometrie-Rechners sind kostenlos verfügbar und machen hochwertige Werkzeuge für alle zugänglich.
Ja, er ist komplett kostenlos. Nutzer können alle Funktionen ohne Kosten nutzen.
Öffnen Sie unsere Webseite, wählen Sie „Neue Geometrie“ und klicken Sie dann auf Werkzeuge wie „Punkt“, „Strecke“ oder „Kreis“, um Formen im Zeichenbereich zu platzieren.
Er wird häufig im Mathematikunterricht eingesetzt und kann auch beim Lehren von Geometrie, Algebra und Analysis unterstützen.
Zeichnen oder importieren Sie die Form, wählen Sie das zu messende Objekt aus und wählen Sie dann Eigenschaften wie Abstand, Länge, Winkel, Umfang oder Fläche. Die Ergebnisse erscheinen im Zeichen- oder Algebra-Bereich.
Ja. Der Geometrie-Rechner ist einfach zu bedienen und hat eine intuitive Benutzeroberfläche – ideal für Anfänger, um schnell loszulegen.
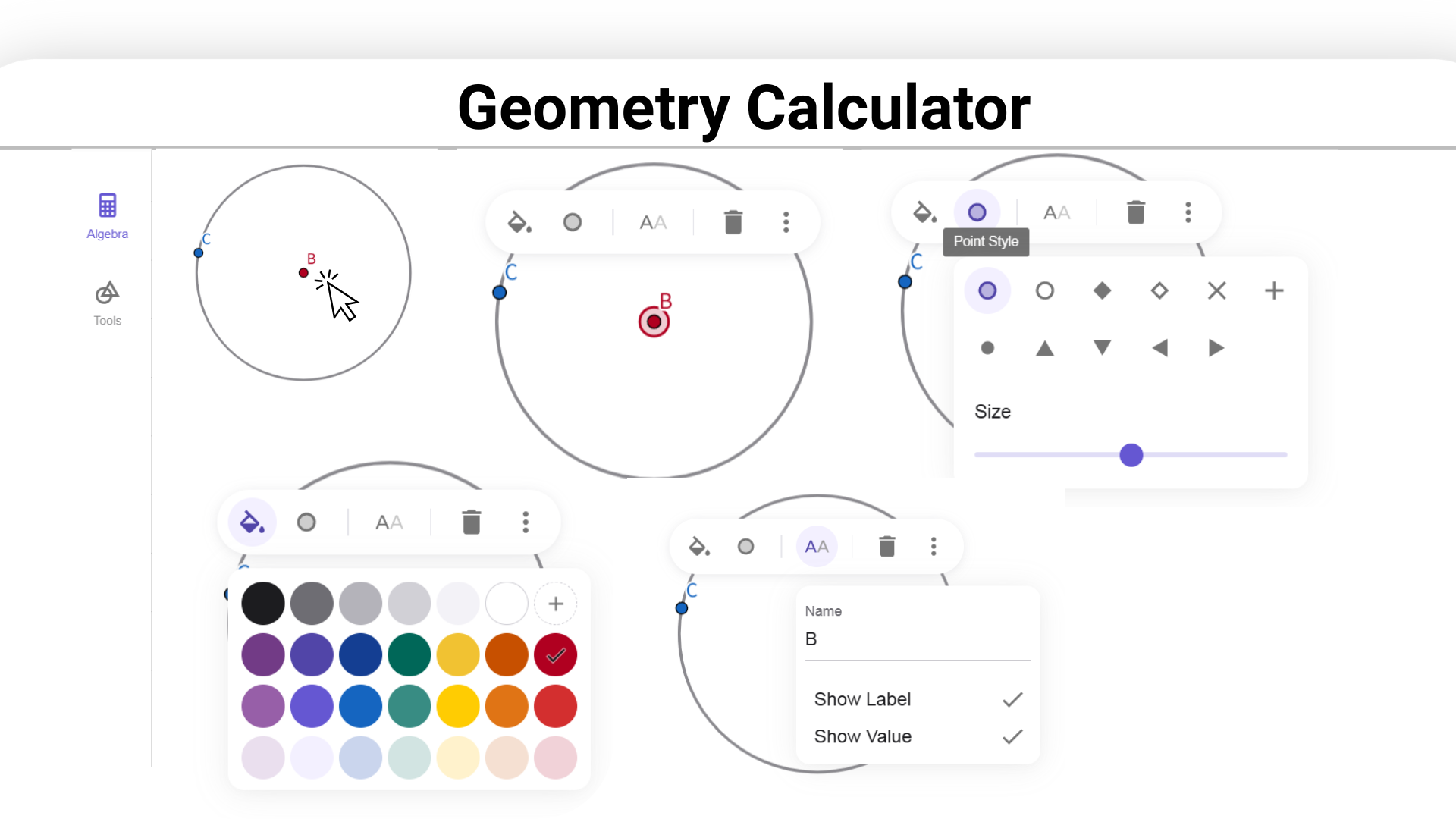
Wählen Sie die Form aus und nutzen Sie das Rechtsklick-Menü oder das Eigenschaftenfeld, um das Aussehen zu bearbeiten, einschließlich Farbe, Linienstil und Füllung.
Unser Geometrie-Rechner verwendet fortschrittliche Algorithmen, um präzise und zuverlässige Ergebnisse zu liefern.
Er hilft Schülern, die Verbindung zwischen Algebra und Geometrie zu erforschen, und unterstützt sie dabei, Aufgaben und Forschungsprojekte effizienter zu erledigen.