Schüler
Der Grafikrechner profitiert von Schülern von der Grundschule bis zur Universität. Es hilft ihnen, mathematische Konzepte zu erfassen und Problemlösungsfähigkeiten zu entwickeln.
Graphing-Rechner
Ein Graphing-Rechner kann Gleichungen lösen und Graphen von Funktionen zeichnen, was Ihnen hilft, die sich ändernden Muster von Funktionen intuitiv und genau zu verstehen.
Was ist ein Grafikrechner?
Der Grafikrechner ist ein leistungsstarkes und technologisch fortschrittliches Zeichenwerkzeug, das uns hilft, Funktionsgraphen zu zeichnen, komplexe Berechnungen durchzuführen und Datenanalysen durchzuführen. Durch die Anpassung von Parametern, um die Transformation von Grafiken zu beeinflussen, wird das mathematische Lernen und die Forschung intuitiver, effizienter und interessanter.
Ersetzen Sie die komplexe manuelle Zeichnung
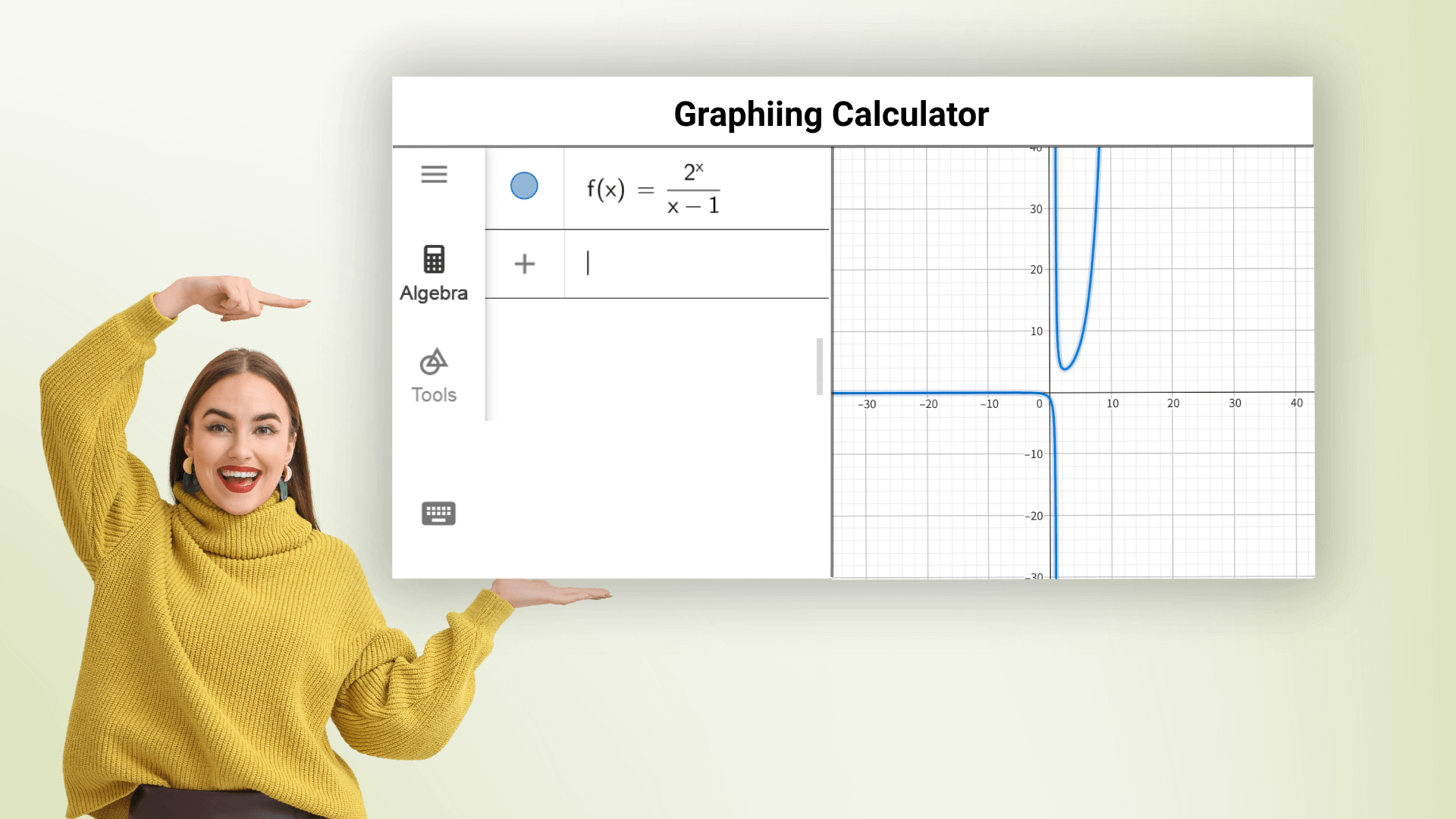
Der Grafikrechner kann verschiedene Funktionsgraphen zeichnen, einschließlich linearer, parabolischer, trigonometrischer und logarithmischer Funktionen, und er kann mehrere Gleichungen gleichzeitig in verschiedenen Farben zeichnen. Geben Sie einfach den Funktionsausdruck ein, um schnell einen genauen Graphen zu erhalten und Funktionstrends und -eigenschaften zu beobachten. Der Online-Grafikrechner hilft jedem, Mathematik zu beherrschen und komplexe Berechnungen zu vermeiden.
Reiche wissenschaftliche Rechenmethoden
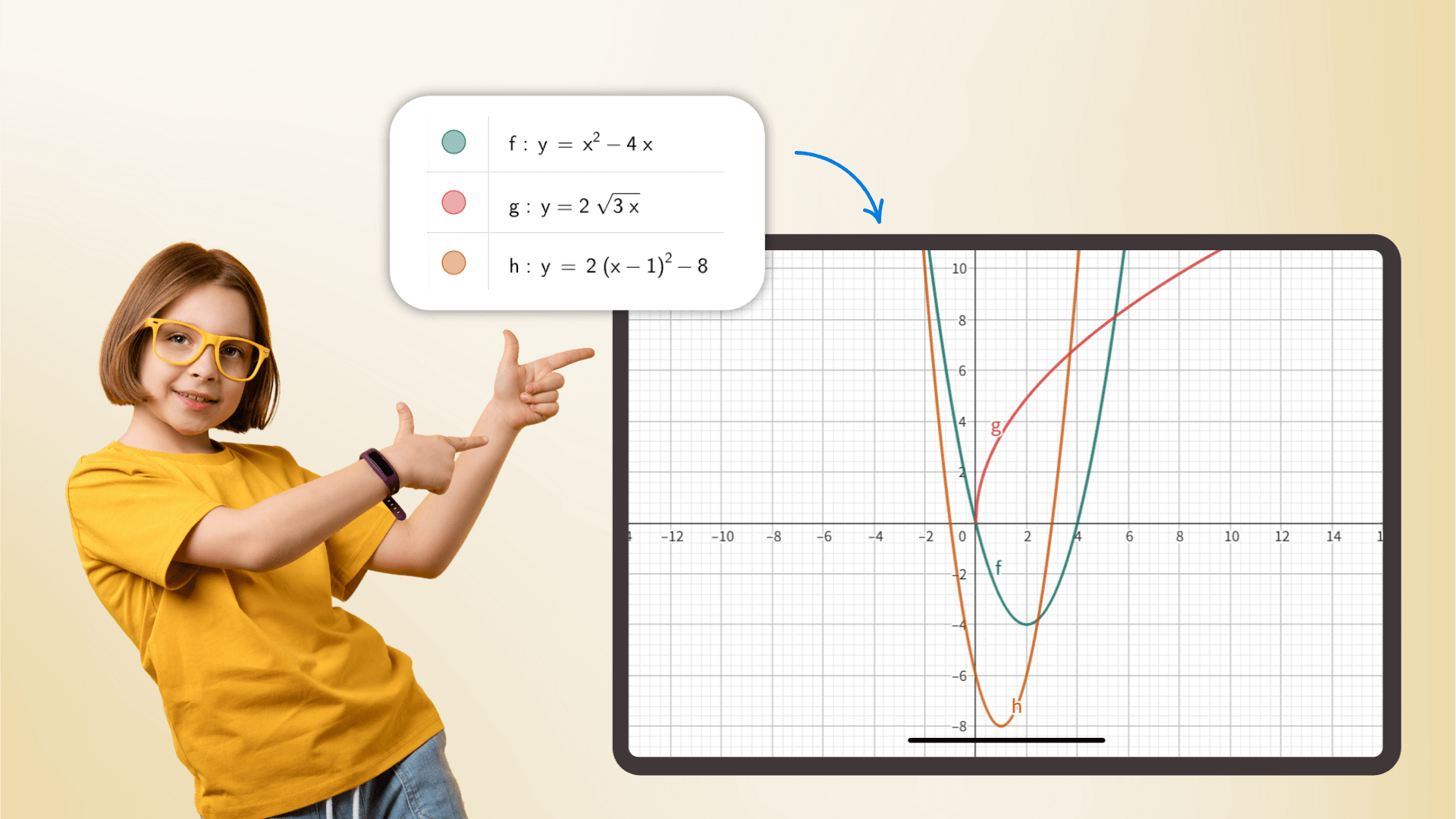
Als wissenschaftlicher Taschenrechner kann er alles von einfacher Arithmetik bis zu fortgeschrittener Mathematik, Kalkül, Wahrscheinlichkeitsstatistik und mehr bewältigen. Mit präzisionsgetriebenen Berechnungen dient er als unverzichtbarer Assistent für Studenten und Forscher gleichermaßen und steigert die Effizienz in akademischen und beruflichen Kontexten.
Intelligentes interaktives Zeichnen
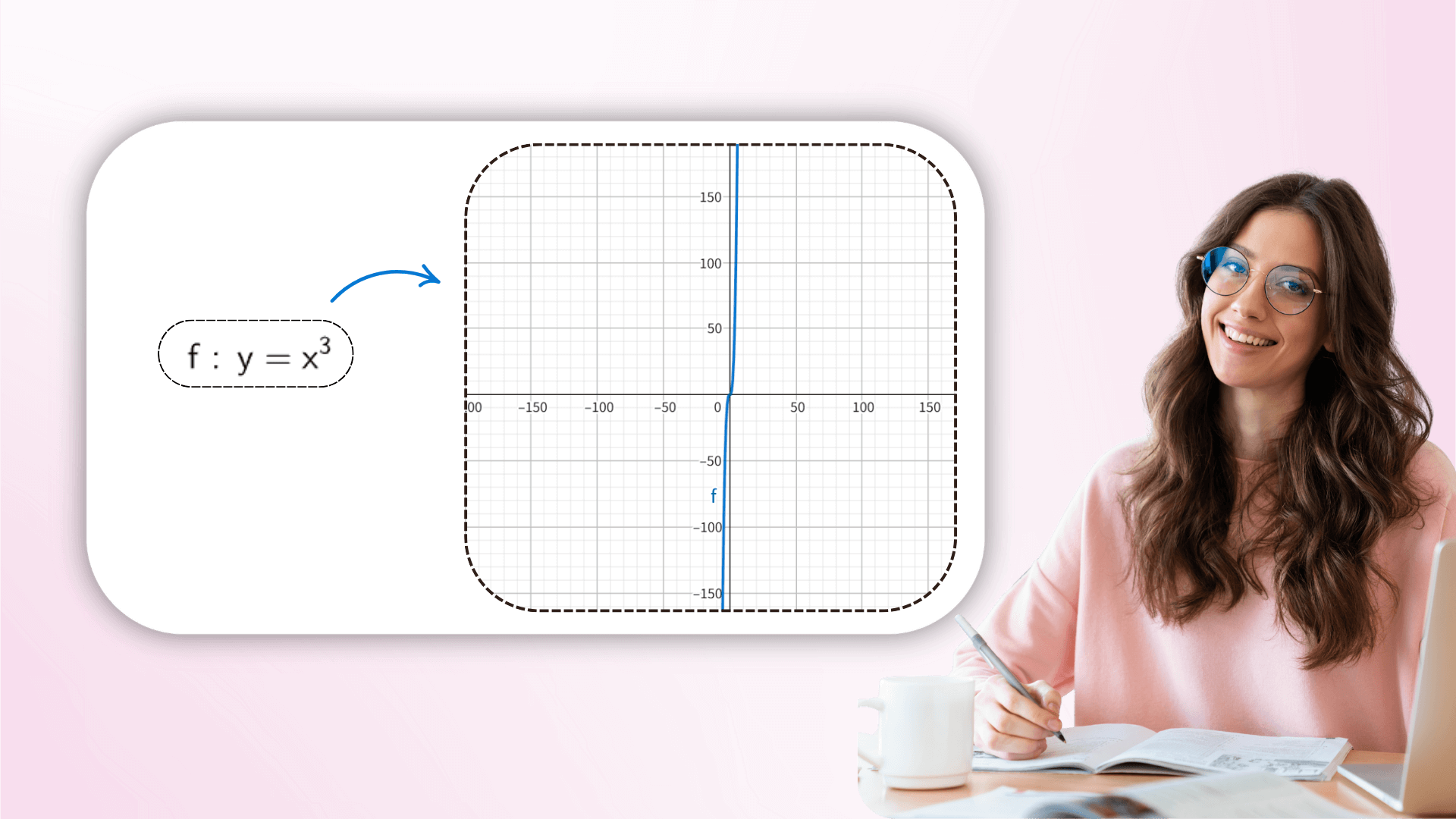
Durch die Einstellung von Parameterwerten in Echtzeit können Benutzer die dynamische Transformation des Bildes beobachten, um zu verstehen, wie die Koeffizienten die Funktionengeometrie beeinflussen, von der linearen Translation bis zu komplexen Transformationen, die abstrakte Formeln mit der Vision verknüpfen. Diese interaktive Erkundung kann das Verständnis mathematischer Gleichungen vertiefen.
Funktionen des Grafikrechners
Interaktives Zeichnen
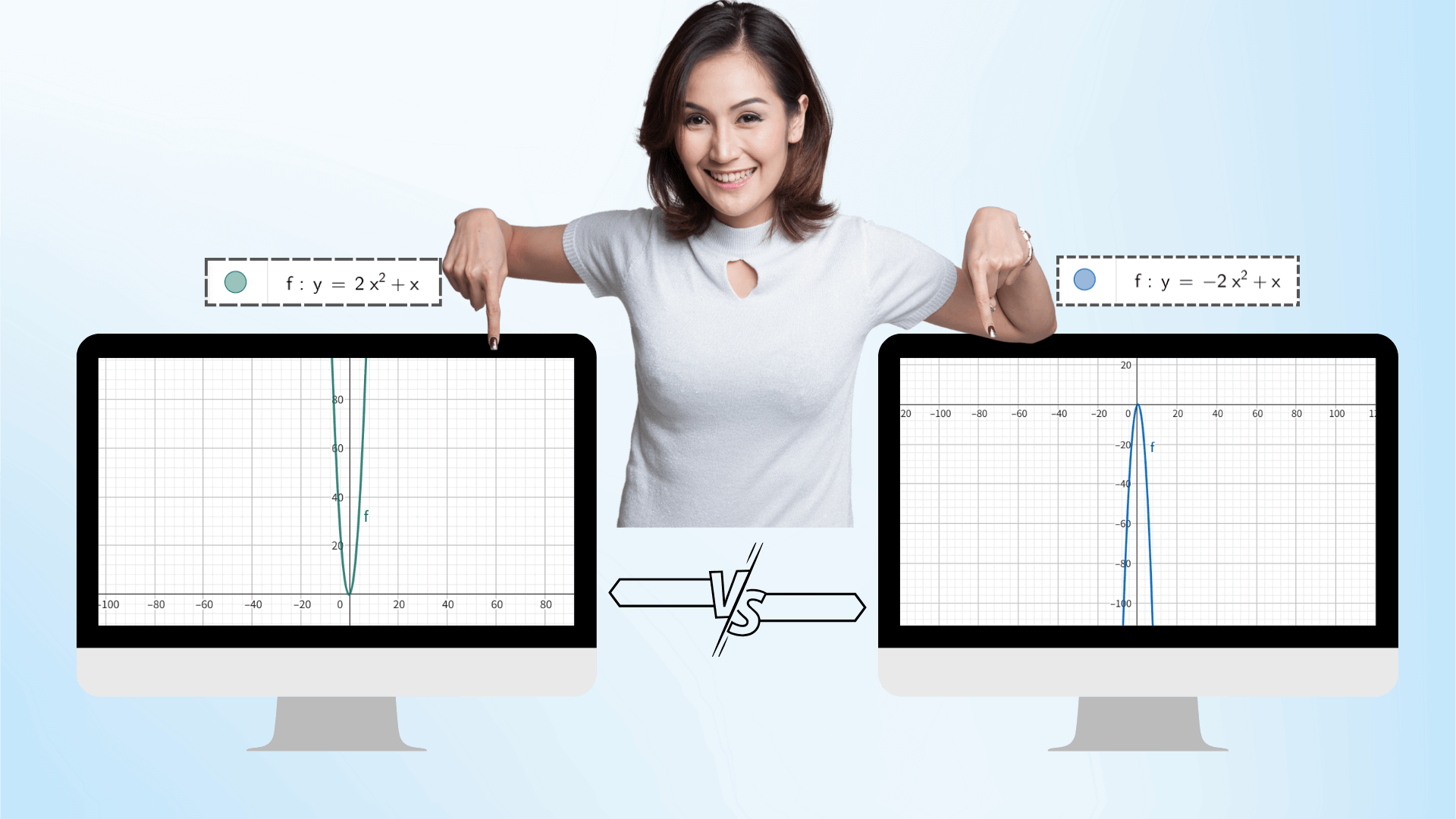
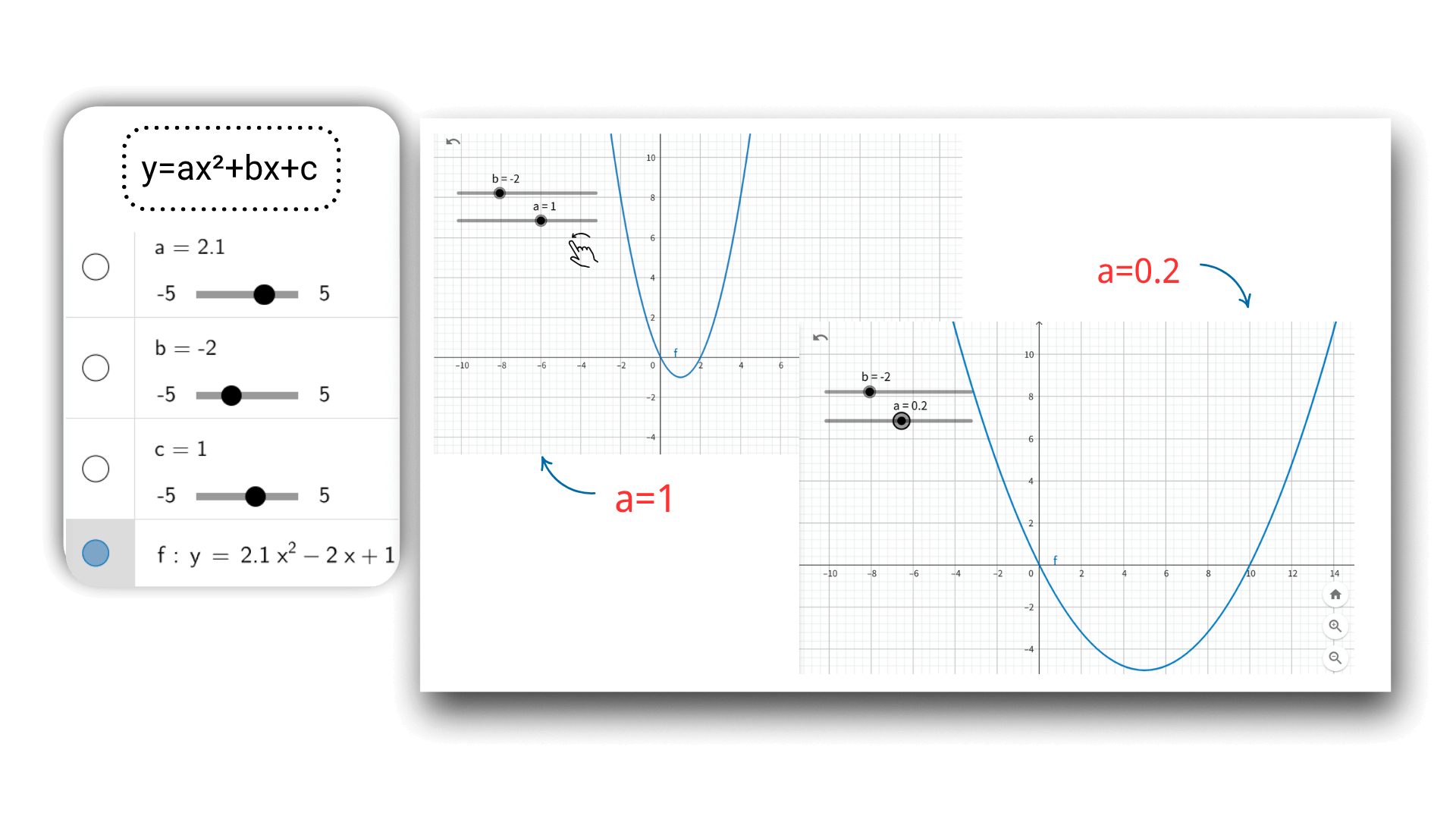
Mit der AI-Grafiktechnologie können Sie nach Eingabe der Funktion die Parameter dynamisch über den Schieberegler anpassen, wie z.B. a, b, c einer quadratischen Funktion. Das Bild wird sich in Echtzeit wie eine Animation verformen, und die Koordinatendaten werden synchron aktualisiert, um den Einfluss von Parameteränderungen auf das Bild intuitiv zu zeigen und die Verbindung zwischen mathematischen Konzepten besser zu verstehen.
Intelligente Datenanalyse
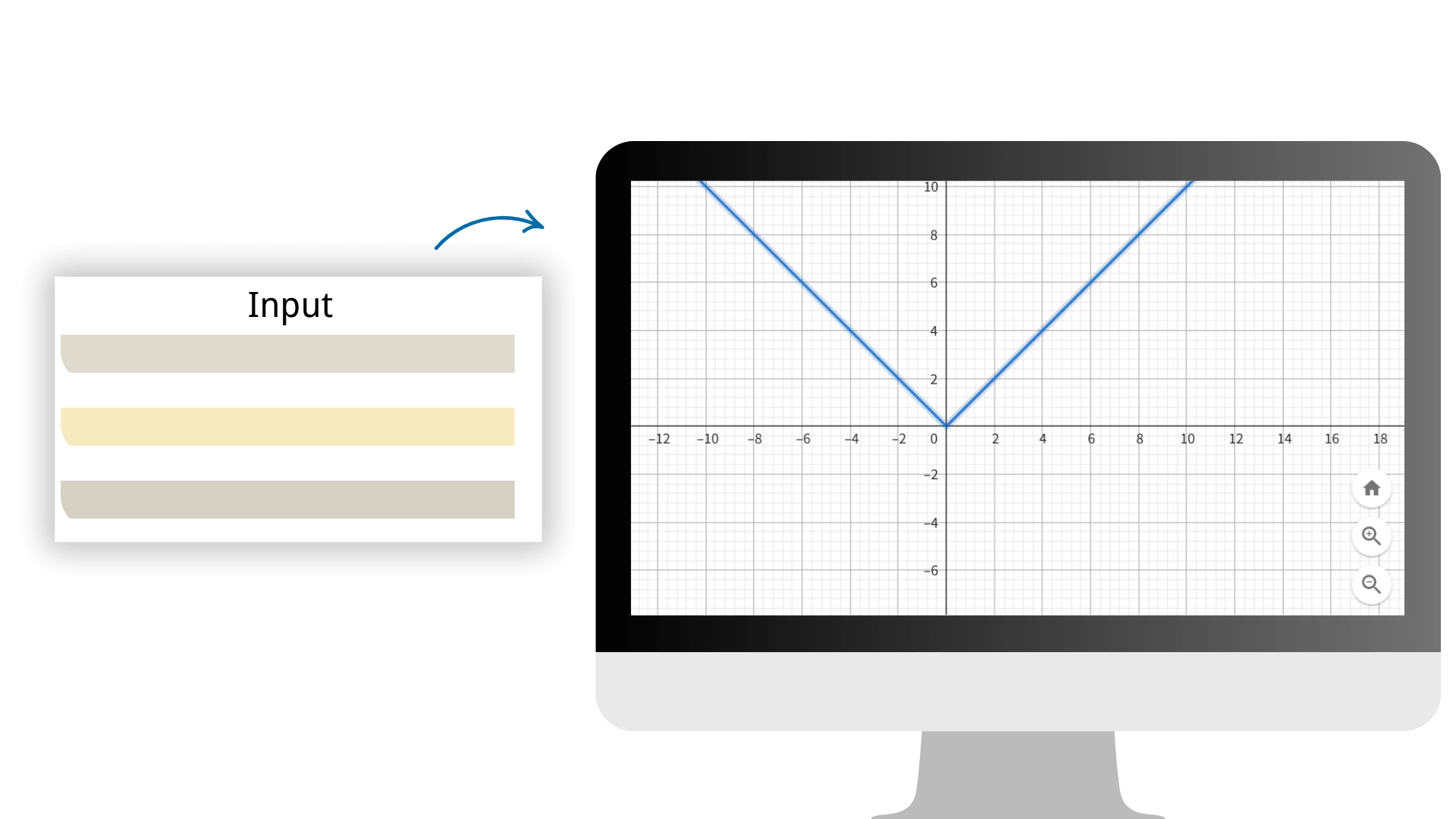
Durch den Einsatz fortschrittlicher Berechnungsalgorithmen stellen wir sicher, dass jedes Berechnungsergebnis eine extrem hohe Genauigkeit aufweist und zuverlässige Datenunterstützung für Ihre mathematische Arbeit bietet. Geben Sie einfach das Array in unseren Bildrechner ein, um mit einem Klick verschiedene Bilder zu generieren.
Automatische Fehlerkorrektur und Vorschläge
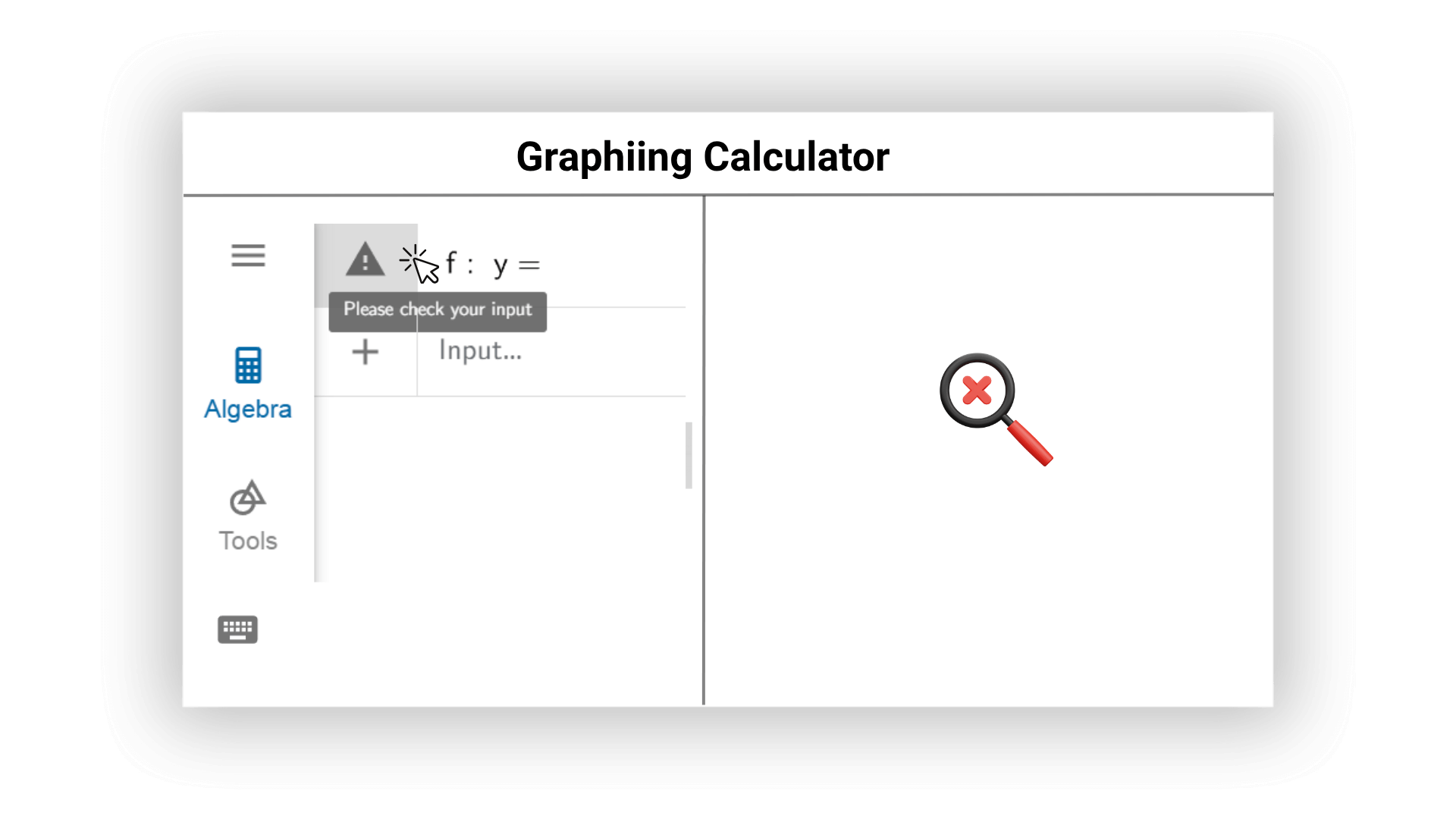
Unser AI-Grafikrechner kann mögliche Fehler in mathematischen Ausdrücken online in Echtzeit überprüfen und proaktiv Vorschläge zur Änderung machen. KI kann Benutzer prompt auf grammatikalische Probleme und unangemessene Eingaben hinweisen, um genaue Berechnungsergebnisse und hohe Rechenleistung zu gewährleisten und Fehler in Bildern und Ergebnissen zu vermeiden.
Wie benutzt man den Grafikrechner?
Step 1
Mathematische Ausdrücke eingeben
Geben Sie die Funktionsausdrücke oder Daten, die Sie analysieren
möchten, in den dafür vorgesehenen Bereich ein, und der
KI-Grafikrechner beginnt sofort mit der Verarbeitung.
Step 2
Grafiken anzeigen
Nach der Berechnung oder Grafikdarstellung können Sie sofort die
generierten Bilder, Daten und Ergebnisse sehen.
Step 3
Mit Grafiken interagieren
Passen Sie Parameter an oder führen Sie weitere Analysen durch,
und die Grafiken werden in Echtzeit aktualisiert.
Anleitung zum Zeichnen klassischer Grafiken
Parameter linearer Gleichungen
Quadratische Polynome
Parameter eines Polynoms
Lineares Gleichungssystem
Ableitungen zeichnen
Ableitung des Sinus
Lineare Ungleichungen
Arbeiten mit Folgen
Visualisierung der Ganzzahladdition
Visualisierung der Multiplikation
1. 
Geben Sie y = m x + b in die Eingabeleiste
ein und drücken Sie die Eingabetaste.
Hinweis:
Der Grafikrechner erstellt beim Drücken von Enter
automatisch Schieberegler für die Parameter m und b. Um die
Schieberegler in der Grafikansicht anzuzeigen, wählen Sie
die deaktivierte Sichtbarkeitsschaltfläche in der
Algebraansicht links neben den Variablen.
2. 
Erstellen Sie den Schnittpunkt A zwischen der Geraden und
der y-Achse.
Hinweis: Sie können entweder das
Schnittpunkt-Werkzeug im Werkzeugkasten für Punkte
verwenden, indem Sie die beiden Objekte auswählen, oder den
Befehl Intersect(f, yAxis) nutzen.
3. Erstellen Sie einen Punkt B im Ursprung, indem Sie das
Schnittpunkt-Werkzeug verwenden und die beiden Achsen
auswählen.
4. 
Wählen Sie das Strecken-Werkzeug aus dem Werkzeugkasten für
Linien und erstellen Sie eine Strecke zwischen den Punkten A
und B, indem Sie beide Punkte auswählen.
Hinweis:
Alternativ können Sie auch den Befehl Segment(A, B)
verwenden.
5. 
Blenden Sie die Punkte A und B aus, indem Sie auf die
entsprechenden aktivierten Sichtbarkeitsschaltflächen links
neben ihren Koordinaten in der Algebraansicht klicken.
6. 
Verwenden Sie das Steigungswerkzeug aus dem
Messwerkzeugkasten, um die Steigung (Dreieck) der Geraden zu
erstellen, indem Sie auf die Gerade klicken.
7. 
Verbessern Sie das Aussehen Ihrer Konstruktion mit der
Stil-Leiste (z. B. erhöhen Sie die Linienstärke der Strecke,
damit sie auf der y-Achse sichtbar ist).
1. Geben Sie f(x) = x^2 in die Eingabeleiste ein und
drücken Sie die Eingabetaste.
Welche Form hat der
Funktionsgraph?
2. 
Verwenden Sie das Verschieben-Werkzeug und wählen Sie die
Funktion aus. Klicken Sie auf die Stil-Leiste und wählen
Sie, die Funktion zu lösen. Sie können die Funktion nun in
der Grafikansicht ziehen und beobachten, wie sich die
Gleichung in der Algebraansicht anpasst.
3. 
Ändern Sie den Funktionsgraphen so, dass die entsprechende
Gleichung passt:
f(x) = (x + 2)²
f(x) = x² - 3
und
f(x) = (x - 4)² + 2.
4. Wählen Sie die Gleichung des Polynoms aus. Verwenden Sie
die Tastatur, um die Gleichung in f(x) = 3 x^2 zu
ändern.
Wie verändert sich der Funktionsgraph?
5. Wiederholen Sie das Ändern der Gleichung, indem Sie
verschiedene Werte für den Parameter eingeben (z. B. 0.5,
-2, -0.8, 3).
1. 
Geben Sie f(x) = a*x³ + b*x² + c*x + d in die
Eingabeleiste ein und drücken Sie die Eingabetaste.
Hinweis: Der Grafikrechner erstellt automatisch
Schieberegler für die Parameter a, b, c und d.
2. Zeigen Sie die Schieberegler in der Grafikansicht an, indem
Sie die deaktivierten Sichtbarkeitsschaltflächen links neben
den entsprechenden Einträgen in der Algebraansicht
auswählen.
3. Verwenden Sie die Schieberegler in der Grafikansicht, um
die Werte der Parameter mit dem Verschieben-Werkzeug auf
a = 0.2, b = -1.2, c = 0.6, d = 2 zu ändern.
4. 
Geben Sie R = Root(f) in die Eingabeleiste ein, um
die Nullstellen des Polynoms anzuzeigen. Die Nullstellen
werden automatisch R1, R2 und R3 genannt.
5. 
Geben Sie E = Extremum(f) ein, um die lokalen
Extrema des Polynoms anzuzeigen.
6. 
Verwenden Sie das Tangenten-Werkzeug, um die Tangenten an
das Polynom durch die Extrema E1 und E2 zu erstellen.
Hinweis: Öffnen Sie den Werkzeugkasten für
spezielle Linien und wählen Sie das Tangenten-Werkzeug.
Wählen Sie nacheinander Punkt E1 und das Polynom aus, um
die Tangente zu erstellen. Wiederholen Sie dies für Punkt
E2.
7. Ändern Sie systematisch die Werte der Schieberegler mit dem
Verschieben-Werkzeug, um zu erforschen, wie die Parameter
das Polynom beeinflussen.
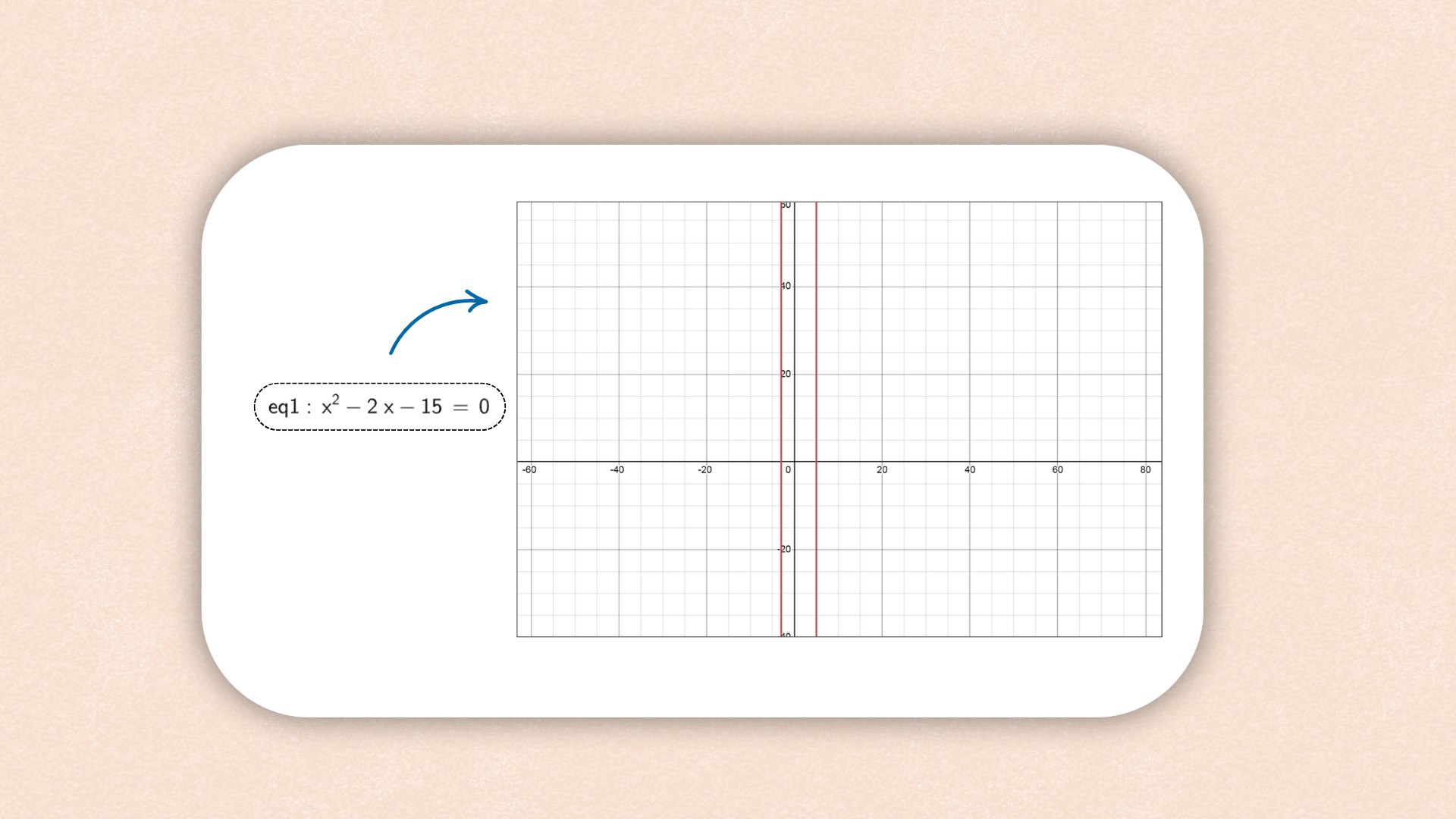
1. Geben Sie die lineare Gleichung
line_1: y = m_1 x + b_1 in die Eingabeleiste ein.
Hinweis: Die Eingabe line_1 ergibt Ihnen
line1.
2. 
Der Grafikrechner erstellt beim Drücken von Enter
automatisch Schieberegler für die Variablen m_1 und
b_1.
3. Zeigen Sie die Schieberegler in der Grafikansicht an, indem
Sie auf die deaktivierten Sichtbarkeitsschaltflächen neben
ihrem Eintrag in der Algebraansicht klicken.
4. Wiederholen Sie die Schritte 1 bis 3 für die Gleichung von
line_2: y = m_2 x + b_2.
5. Verwenden Sie die Stil-Leiste, um die Farbe beider Geraden
und ihrer Schieberegler zu ändern.
6. 
Verwenden Sie das Text-Werkzeug und erstellen Sie einen
dynamischen Text, indem Sie Line 1: im erscheinenden
Dialog eingeben und line_1 aus der Liste der Objekte
im Tab Objekte des erweiterten Bereichs auswählen.
7. Erstellen Sie einen dynamischen Text mit dem statischen
Teil Line 2: und wählen Sie line_2 aus der
Liste der Objekte im Tab Objekte des erweiterten
Bereichs.
8. Verwenden Sie die Stil-Leiste, um die Farbe der Texte an
die entsprechenden Geraden anzupassen.
9. Konstruiere den Schnittpunkt A von line_1 und
line_2, entweder mit dem Schnittpunkt-Werkzeug oder
indem Sie den Befehl Intersect(line_1, line_2) in die
Eingabeleiste eingeben.
10. Geben Sie xcoordinate = x(A) in die Eingabeleiste
ein.
Hinweis: x(A) gibt Ihnen die x-Koordinate des
Schnittpunkts A.
11. Definieren Sie außerdem ycoordinate = y(A).
Hinweis: y(A) gibt Ihnen die y-Koordinate des
Schnittpunkts A.
12. Erstellen Sie einen dynamischen Text mit dem statischen
Teil Lösung: x = und wählen Sie
xcoordinate aus der Liste der Objekte im Tab
Objekte.
13. Erstellen Sie einen dynamischen Text mit dem statischen
Teil y = und wählen Sie ycoordinate aus der
Liste der Objekte im Tab Objekte.
14. Fixieren Sie die Texte, damit sie nicht versehentlich
verschoben werden können, indem Sie die Texte auswählen und
die Stil-Leiste öffnen.
1. Geben Sie das Polynom f(x) = x^2/2 + 1 in die
Eingabeleiste ein.
2. 
Erstellen Sie einen neuen Punkt A auf der Funktion
f.
Hinweis: Punkt A kann nur entlang der Funktion
verschoben werden.
3. Erstellen Sie die Tangente g an die Funktion
f durch den Punkt A.
4. Erstellen Sie die Steigung der Tangente g mit
m = Slope(g).
5. Definieren Sie den Punkt S = (x(A), m).
Hinweis: x(A) gibt Ihnen die x-Koordinate von
Punkt A.
6. Verbinden Sie die Punkte A und S mit einer
Strecke.
7. 
Aktivieren Sie die Spur von Punkt S und bewegen Sie
Punkt A.
Hinweis: Rechtsklick auf Punkt S (MacOS:
Ctrl-Klick, Tablet: langes Tippen) und wählen Sie Spur
anzeigen.
1. Geben Sie die Funktion f(x) = sin(x) in die
Eingabeleiste ein.
2. 
Klicken Sie mit der rechten Maustaste auf die Grafikansicht
und wählen Sie Grafik... . Wählen Sie den Tab x-Achse und
ändern Sie die Einheit auf π.
3. Erstellen Sie einen neuen Punkt A auf der Funktion
f.
Hinweis: Punkt A kann nur entlang der Funktion
verschoben werden.
4. Erstellen Sie die Tangente g an die Funktion
f durch Punkt A.
5. Erstellen Sie die Steigung der Tangente g mit dem
Steigungswerkzeug.
6. Definieren Sie den Punkt S = (x(A), m).
Hinweis: x(A) gibt Ihnen die x-Koordinate von
Punkt A.
7. Verbinden Sie die Punkte A und S mit einer
Strecke.
8. Aktivieren Sie die Spur von Punkt S und bewegen Sie
Punkt A.
Hinweis: Rechtsklick auf Punkt S (MacOS:
Ctrl-Klick, Tablet: langes Tippen) und wählen Sie Spur
anzeigen.
9. Rechtsklick (MacOS: Ctrl-Klick, Tablet: langes Tippen) auf
Punkt A und wählen Sie Animation aus dem
Kontextmenü.
Hinweis: Unten links in der Grafikansicht
erscheint eine Animationsschaltfläche. Damit können Sie
die Animation pausieren oder fortsetzen.
1. Geben Sie a x + b y ≤ c in die Eingabeleiste ein und
drücken Sie Enter.
Hinweis: Sie können die
virtuelle Tastatur verwenden, um das ≤-Symbol einzugeben.
Der Grafikrechner erstellt automatisch Schieberegler für die
Parameter a, b und c.
2. Verwenden Sie das Verschieben-Werkzeug, um die Werte der
Schieberegler so einzustellen, dass a = 1, b = 1 und c =
3.
3. Ändern Sie die Schrittweite der Schieberegler auf 1.
Hinweis:
Wählen Sie die Zahl a aus und öffnen Sie die Stil-Leiste der
Grafikansicht.
Öffnen Sie die Einstellungen der Zahl a und wählen Sie den
Tab Schieberegler.
Setzen Sie die Schrittweite auf 1 und wiederholen Sie dies
für die Zahlen b und c.
4. Ziehen Sie den Hintergrund der Grafikansicht, um den
Ursprung in die Mitte zu verschieben.
5. 
Zoomen Sie heraus, um einen größeren Teil des
Koordinatensystems auf dem Bildschirm sichtbar zu
machen.
6. Setzen Sie den Abstand zwischen den Markierungen auf den
Achsen auf 1.
Hinweis:
Stellen Sie sicher, dass kein Objekt ausgewählt ist, bevor
Sie die Stil-Leiste der Grafikansicht öffnen.
Öffnen Sie die Einstellungen der Achsen.
Wählen Sie den Tab x-Achse und setzen Sie den Abstand auf 1.
Wiederholen Sie dies für den Tab y-Achse.
1. Geben Sie
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) in
die Eingabeleiste ein und drücken Sie Enter.
2. Erstellen Sie einen Schieberegler s für eine Zahl
mit Intervall von 1 bis 10 und Schrittweite 1.
3. Geben Sie Sequence((i, i), i, 0, s) in die
Eingabeleiste ein und drücken Sie Enter.
4. Bewegen Sie den Schieberegler s, um die Konstruktion
zu überprüfen.
1. Öffnen Sie die Einstellungen der Grafikansicht über die
Stil-Leiste.
2. Stellen Sie im Tab x-Achse den Abstand der Teilstriche auf
1, indem Sie das Kästchen Abstand aktivieren und 1 in das
Textfeld eingeben.
3. Stellen Sie im Tab Basis das Minimum der x-Achse auf -11
und das Maximum auf 11.
4. Deaktivieren Sie im Tab y-Achse die Anzeige der y-Achse und
schließen Sie die Einstellungen.
5. Erstellen Sie zwei Schieberegler a und b,
beide mit Intervall -5 bis 5 und Schrittweite 1.
6. 
Zeigen Sie den Wert der Schieberegler anstelle ihrer Namen
mit der Stil-Leiste an.
7. Erstellen Sie die Punkte A = (0, 1) und
B = A + (a, 0).
Hinweis: Der Abstand von Punkt B zu Punkt A wird
durch den Schieberegler a bestimmt.
8. 
Erstellen Sie einen Vektor u = Vector(A, B), der die
Länge a hat.
9. Erstellen Sie die Punkte C = B + (0, 1) und
D = C + (b, 0).
10. Erstellen Sie den Vektor v = Vector(C, D), der die
Länge b hat.
11. Erstellen Sie den Punkt R = (x(D), 0).
Hinweis: Die Eingabe x(D) gibt Ihnen die
x-Koordinate von Punkt D. Somit zeigt Punkt R das Ergebnis
der Addition auf der Zahlengeraden an.
12. Erstellen Sie den Punkt Z = (0, 0).
13. Erstellen Sie drei Strecken c = Segment(Z, A),
d = Segment(B, C) und e = Segment(D, R).
14. Verwenden Sie die Stil-Leiste, um Ihre Konstruktion zu
verbessern (z. B. Farbe der Schieberegler und Vektoren
anpassen, Linienstil ändern, Schieberegler fixieren,
Beschriftungen und Punkte ausblenden).
1. Erstellen Sie einen horizontalen Schieberegler mit dem
Namen Columns für eine Zahl mit Intervall von 1 bis
10, Schrittweite 1 und Breite 300.
Hinweis:
Sie können die Breite des Schiebereglers im Tab
Einstellungen unter Schieberegler ändern.
2. 
Erstellen Sie einen neuen Punkt A.
3. 
Konstruiere die Strecke f mit der gegebenen Länge
Columns ausgehend von Punkt A.
4. Bewegen Sie den Columns-Schieberegler, um die Strecke mit
der angegebenen Länge zu beobachten.
5. 
Konstruiere eine Senkrechte g zur Strecke f durch
Punkt A.
6. Konstruiere eine Senkrechte h zur Strecke f durch
Punkt B.
7. Erstellen Sie einen vertikalen Schieberegler mit dem Namen
Rows für eine Zahl mit Intervall von 1 bis 10,
Schrittweite 1 und Breite 300.
Hinweis: Sie
können die Ausrichtung des Schiebereglers im
Schieberegler-Dialog unter dem Tab Schieberegler
auswählen.
8. 
Erstellen Sie einen Kreis c mit Mittelpunkt A und
Radius Rows.
9. Bewegen Sie den Rows-Schieberegler, um den Kreis mit dem
angegebenen Radius zu beobachten.
10. Schneiden Sie Kreis c mit Gerade g, um den Schnittpunkt
C zu erhalten.
Hinweis: Wenn Sie das
Schnittpunkt-Werkzeug auswählen, klicken Sie auf den
Schnittpunkt oberhalb von Punkt A, um nur diesen Punkt zu
erstellen.
11. 
Erstellen Sie eine Parallele i zur Strecke f durch
den Schnittpunkt C.
12. Schneiden Sie die Geraden i und h, um den Schnittpunkt
D zu erhalten.
13. 
Konstruiere das Polygon ABDC.
14. 
Blenden Sie alle Geraden, Kreis c und Strecke f aus.
15. Blenden Sie die Beschriftungen der Strecken mit der
Stil-Leiste aus.
16. Setzen Sie beide Schieberegler Columns und Rows auf den
Wert 10.
17. Erstellen Sie eine Liste vertikaler Strecken mit:Sequence(Segment(A + i*(1, 0), C + i*(1, 0)), i, 1,
Columns)
Hinweis: A + i*(1, 0) gibt eine Reihe von Punkten an, die
bei Punkt A beginnen und jeweils den Abstand 1 haben.
C + i*(1, 0) gibt eine Reihe von Punkten an, die bei
Punkt C beginnen und jeweils den Abstand 1 haben.
Segment(A
+ i*(1, 0), C + i*(1, 0)) erstellt eine Liste von Strecken
zwischen diesen Punktpaaren. Beachten Sie, dass die
Endpunkte der Strecken in der Grafikansicht nicht angezeigt
werden.
Der Schieberegler Column bestimmt die Anzahl
der erstellten Strecken.
18. Erstellen Sie eine Liste horizontaler Strecken.Sequence(Segment(A + i*(0, 1), B + i*(0, 1)), i, 1,
Rows)
19. Bewegen Sie die Schieberegler Columns und Rows, um die
Konstruktion zu beobachten.
20. Fügen Sie statischen und dynamischen Text ein, um die
Multiplikationsaufgabe mit den Werten von Columns und Rows
als Faktoren darzustellen:text1: Columnstext2: *text3: Rowstext4: =
21. Berechnen Sie das Ergebnis der Multiplikation:
result = Columns * Rows
22. Fügen Sie den dynamischen Text5 ein:
result
23. Blenden Sie die Punkte A, B, C und D aus.
24. Verbessern Sie Ihre Konstruktion mit der Stil-Leiste.
Anwendungsszenarien des Grafikrechners
Mathematikunterricht
Der KI-Grafikrechner ist ein leistungsstarker Assistent für Schüler, um Mathematik zu lernen. Von der Mittelstufe bis zur Universität ist es Algebra, Geometrie, Kalkül oder Statistikkurse, die den Schülern helfen können, mathematische Kenntnisse besser zu verstehen und zu beherrschen und die Lerneffizienz und Noten zu verbessern. Lehrer können ihn verwenden, um Unterrichtsdemonstrationen durchzuführen und lebendige Unterrichtsmaterialien zu erstellen, um das Interesse und die Begeisterung der Schüler am Lernen zu wecken.
Wissenschaftliche Forschung
Es bietet Forschern leistungsstarke mathematische Werkzeuge, um die Datenverarbeitung, die experimentelle Analyse, den Modellbau und die theoretische Verifizierung zu erleichtern. In verschiedenen wissenschaftlichen Bereichen wie Physik, Chemie, Biologie und Ingenieurwissenschaften können Grafikrechner verwendet werden, um komplexe mathematische Operationen und Datenanalysen schnell und präzise abzuschließen und die reibungslose Entwicklung der wissenschaftlichen Forschung zu unterstützen.
Geschäfts- und Datenanalyse
Verwenden Sie den Grafikrechner, um Angebots- und Nachfragekurven, Wachstumsmodelle, etc. zu zeichnen, analysieren Sie den Schnittpunkt von Grenzkosten- und Erlösfunktionen und unterstützen Sie bei unternehmerischen Entscheidungen.
Wer kann unseren Grafikrechner verwenden?
- Schüler
- Lehrer
- Forscher
- Datenanalyst
- Software-Ingenieur
- Designer
Lehrer
Mathematiklehrer können den Grafikrechner verwenden, um Unterrichtsmaterialien zu erstellen und Konzepte und Problemlösungsprozesse zu demonstrieren, um die Unterrichtseffektivität und -interaktion zu verbessern.
Forscher
Forscher in verschiedenen Bereichen verlassen sich auf ihn für komplexe mathematische Berechnungen und Datenanalysen. Der Grafikrechner online beschleunigt präzise Ergebnisse der Forschung.
Datenanalyst
Sagen Sie auf Wiedersehen zu mühsamen manuellen Zeichnungen, generieren Sie professionelle Datenvisualisierungsdiagramme mit einem Klick, zeichnen Sie Funktionengraphen online, kommentieren Sie Mittelwert und Varianz in Echtzeit, passen Sie Regressionskurven dynamisch an und vervollständigen Sie die Datenintegration und -analyse effizient.
Software-Ingenieur
Grafikrechner helfen Software-Ingenieuren, Filteralgorithmen zu visualisieren und Renderingparameter zu optimieren, um eine pixelgenaue Funktion zu gewährleisten.
Architekturdesigner
Für Architekturdesigner sind Grafikrechner parametrische Designkraftwerke, geben Sie Kurvengleichungen ein, um Funktionen/Verdrängungsgraphen zu generieren, validieren Sie visuell die Strukturmechanik und verkürzen Sie die Designzyklen.
Vorteile der Funktionalität von Decopy's Graphikrechner
Vollständig kostenlos zu verwenden
Alle Funktionen erfordern keine Registrierung oder Zahlung und Sie können sie jederzeit verwenden.
Hochpräziser Algorithmus
Beim Berechnen von fortgeschrittenen Problemen wie Matrixdeterminanten und Integralen muss eine hohe Genauigkeit aufrechterhalten werden, um Fehler in der wissenschaftlichen Forschung zu vermeiden.
Datenschutz und Sicherheit
Die Berechnung wird vollständig im Browser durchgeführt, keine Daten werden hochgeladen und die Seite wird bei Schließung gelöscht.
Jederzeit verfügbar
Kein Download und keine Installation notwendig, sofort auf Mobiltelefonen und Computern nutzbar.
Keine Werbeunterbrechungen
Konzentrieren Sie sich auf das Wesentliche des Lernens, keine Pop-ups, keine Werbung, und verbessern Sie Ihre Konzentration.
Unterstützung für alle Szenarien
Ob akademisch, wissenschaftlich, im Büro oder in technischen Anwendungen, wir können Ihre grafischen Rechenbedürfnisse erfüllen.
Bewertungen des Decopy Graphing Calculators
Sarah Johnson
Universitätsstudentin
Robert Thompson
Mathematiklehrer
David Wilson
Finanzanalyst
Häufig gestellte Fragen (FAQs)
Sie müssen sich nicht registrieren oder Software herunterladen. Gehen Sie einfach auf unsere Website in Ihrem Browser und beginnen Sie mit dem leistungsfähigen Graphing Calculator-Tool. Sie können es sofort nutzen.
Ja, unser künstliche Graphing Calculator ist komplett kostenlos. Trotzdem beschränkt er keine Kernfunktionen. Sie können alle Grafik-, Berechnungs- und Datenanalysefunktionen vollständig nutzen, ohne Kosten zu entrichten. Wir möchten ein bequemes und effizientes Mathematik-Tool für jeden bereitstellen.
Wir priorisieren die Sicherheit und den Datenschutz Ihrer Daten. Alle Ihre Berechnungen, Grafiken und Eingabedaten werden lokal in Ihrem Browser verarbeitet und werden niemals auf unseren Servern hochgeladen oder gespeichert. Sie können es mit Vertrauen nutzen, wissen Sie, dass Ihre Daten sicher sind.
Um eine Funktion einzugeben, tippen Sie einfach die Formel in das Eingabefeld auf der Startseite ein. Zum Beispiel geben Sie 'y=2x^2' oder 'f(x)=sin(x)' ein. Der Calculator wird Ihre Eingabe automatisch verarbeiten und die Grafik anzeigen.
Ja, der künstliche Graphing Calculator kann eine Vielzahl von Funktionen handhaben, von einfachen linearen Gleichungen bis hin zu fortgeschrittenen wie Integralen, Ableitungen und multivariablen Gleichungen. Er eignet sich sowohl für grundlegende als auch für fortgeschrittene mathematische Anforderungen, was ihn ideal für Studenten und Fachleute macht.
Ja, er ist vollständig auf mobilen Geräten zugänglich. Sie können ihn auf Smartphones oder Tablets verwenden, und er ist für alle Bildschirmgrößen optimiert, um eine nahtlose Erfahrung zu garantieren, wo immer Sie sind.
↑