Free Equation Solver – Step-by-Step Math Calculator
Free equation calculator solves linear, quadratic, and system of equations from text or image. Includes graphs, roots, and alternate forms.
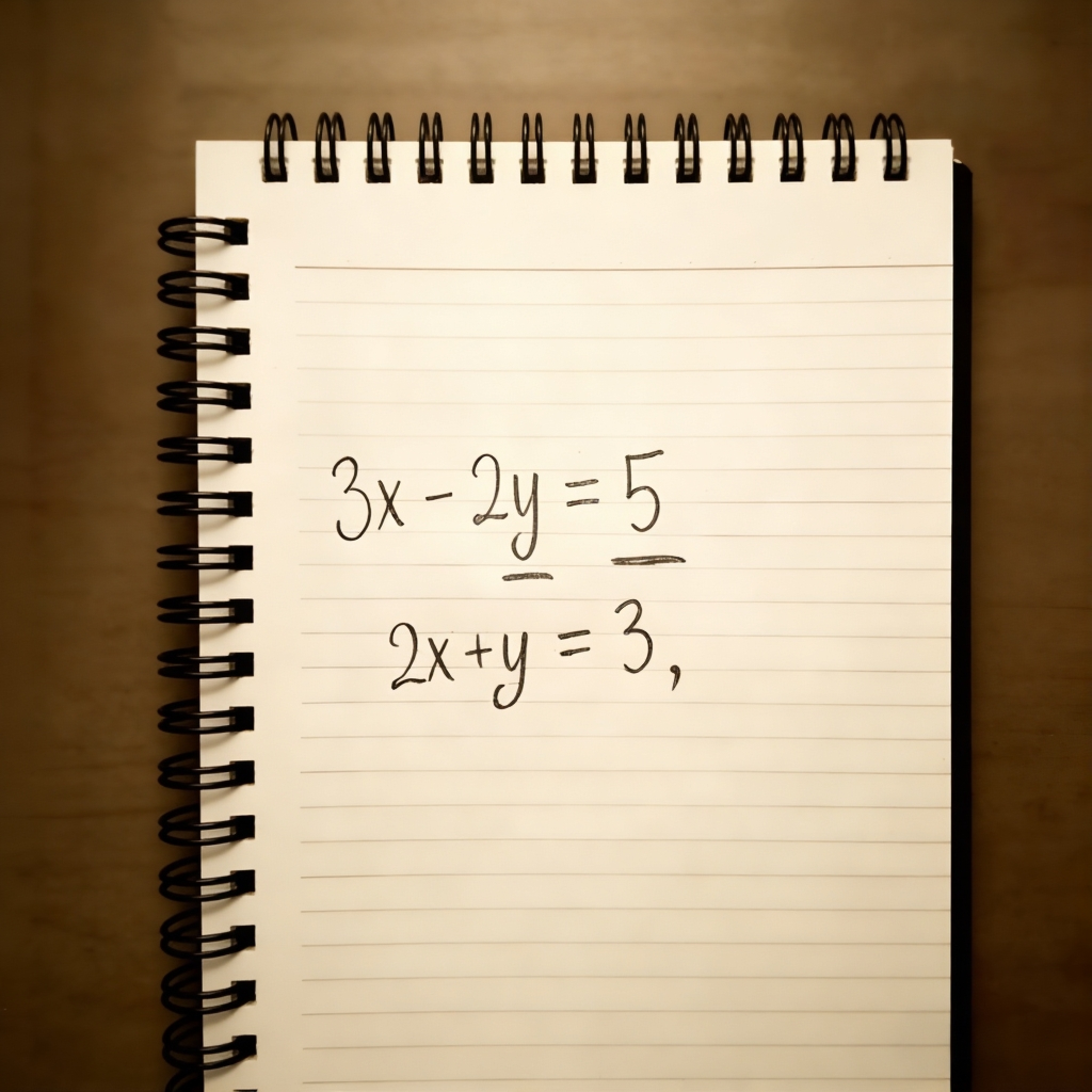
What Is an Equation?
An equation is a mathematical statement containing unknown
variables. Solving equations means finding the values of unknowns
by establishing a relationship between known and unknown
quantities. Common types of math equations include linear
equations, quadratic equations, trigonometric equations,
logarithmic equations, and cubic equations.
Equations
are essential in mathematics, physics, engineering, and economics.
They are powerful tools for solving real-world problems and
understanding complex systems.
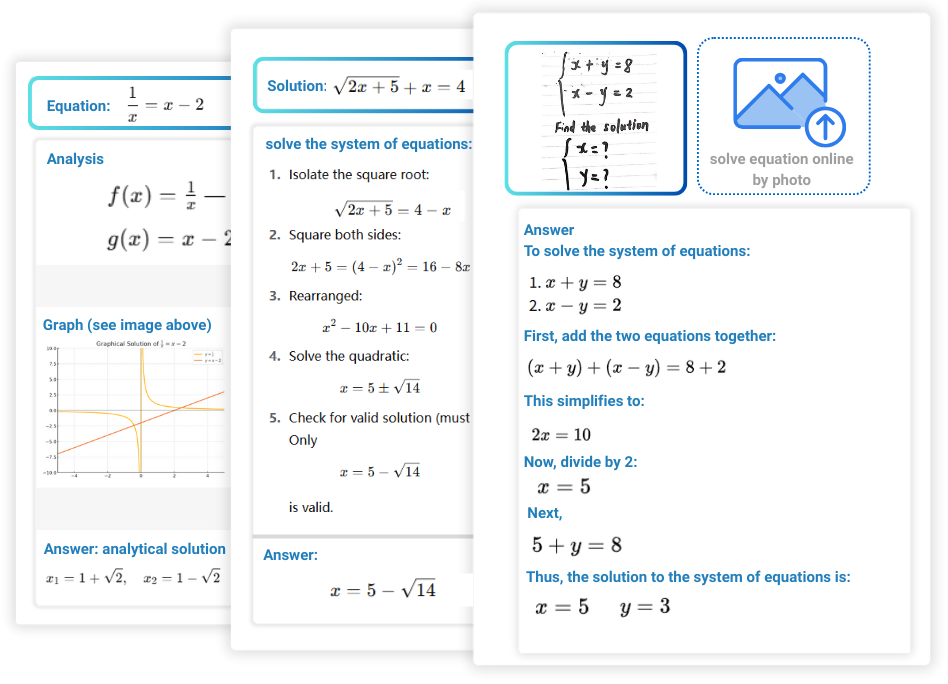
What Is an Equation Calculator?
An equation calculator is an AI-powered tool for solving math equations. It analyzes input using algorithms to quickly and accurately solve various types of equations and systems of equations. Users can type in equations or upload photos containing equations. Decopy AI equation solver will automatically recognize the content, apply standard solving methods, and display the step-by-step solutions.
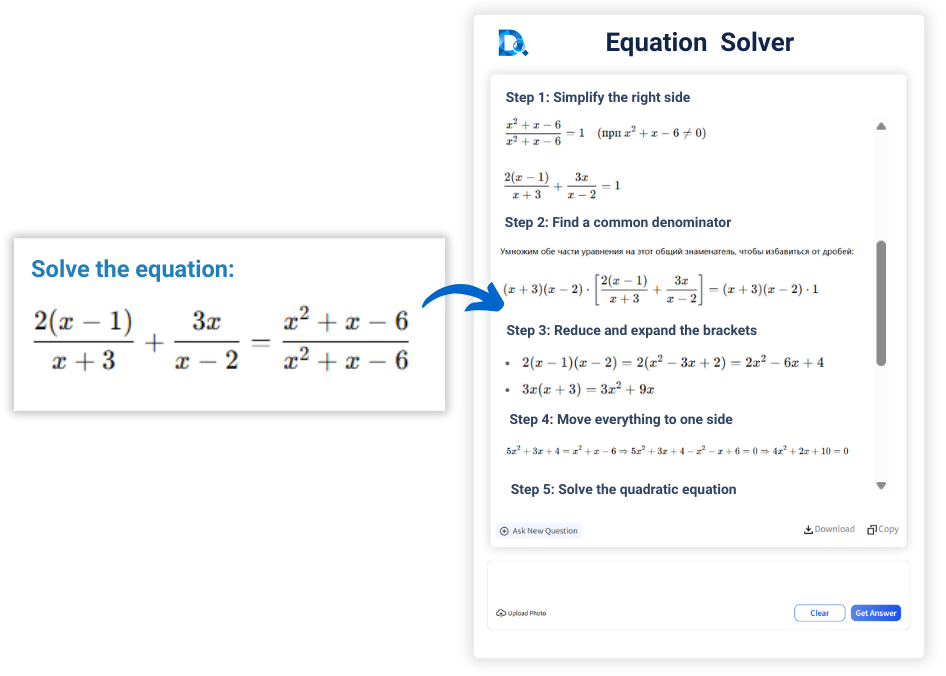
How to Solve Equations?
Traditionally, solving equations requires manual setup,
transformations, and calculations, such as factoring, using the
discriminant, or Gaussian elimination. For higher-degree equations
or complex nonlinear systems, more advanced mathematical methods
and numerical techniques are needed.
With an online
equation calculator, you can simply upload a photo of the equation
or enter it directly. The AI math equations solver will quickly
provide accurate answers. To make the process easier to
understand, Decopy AI equation calculator simulates human solving
methods—such as elimination, substitution, or the quadratic
formula—and shows all the step-by-step solutions.
How Does Decopy AI Equation Calculator Work?
Decopy AI equation calculator is powered by an advanced AI math engine
that combines algebra, numerical analysis, and algorithmic
optimization.
When users input or upload math
equations, the system automatically detects the equation type
(such as linear equations, quadratic equations, trigonometric, or
logarithmic) and selects the best solving method accordingly:
For
linear equations and systems of equations, it uses Gaussian
elimination or matrix methods for fast solving.
For
quadratic equations, it applies the discriminant-based quadratic
formula for step-by-step solving.
For trigonometric,
logarithmic, and cubic equations, it uses standard
transformations, factoring, or numerical approximations.
For
complex nonlinear systems, it applies numerical methods or
advanced solvers.
This equation solver provides final
answers and shows step-by-step solutions to help users understand
the mathematical principles.
Features of Equation Calculator
Quickly and accurately solve math equations online using photos or manual input. Supports all types with step-by-step analysis.
Photo solve
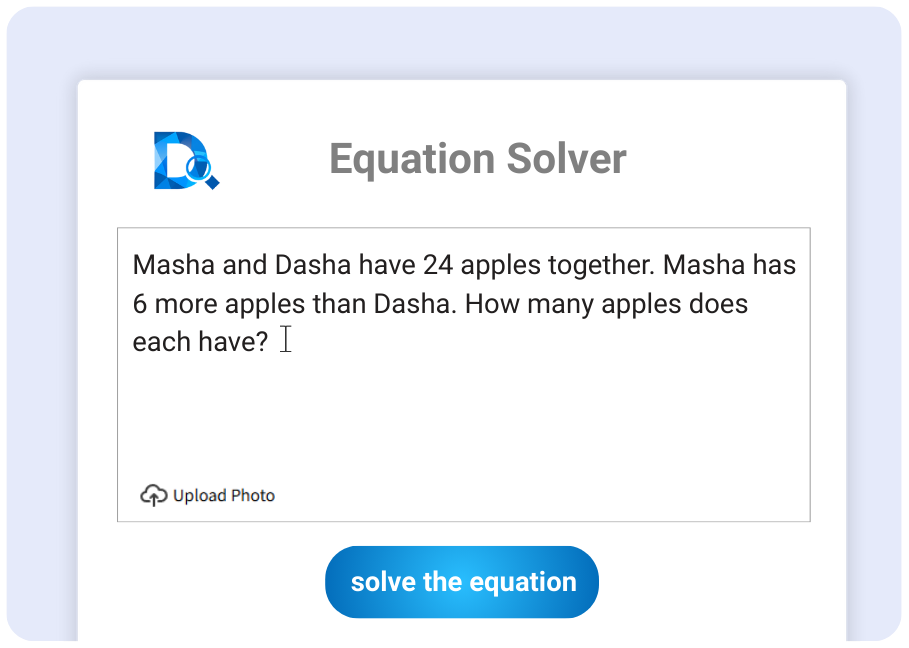
Manual input
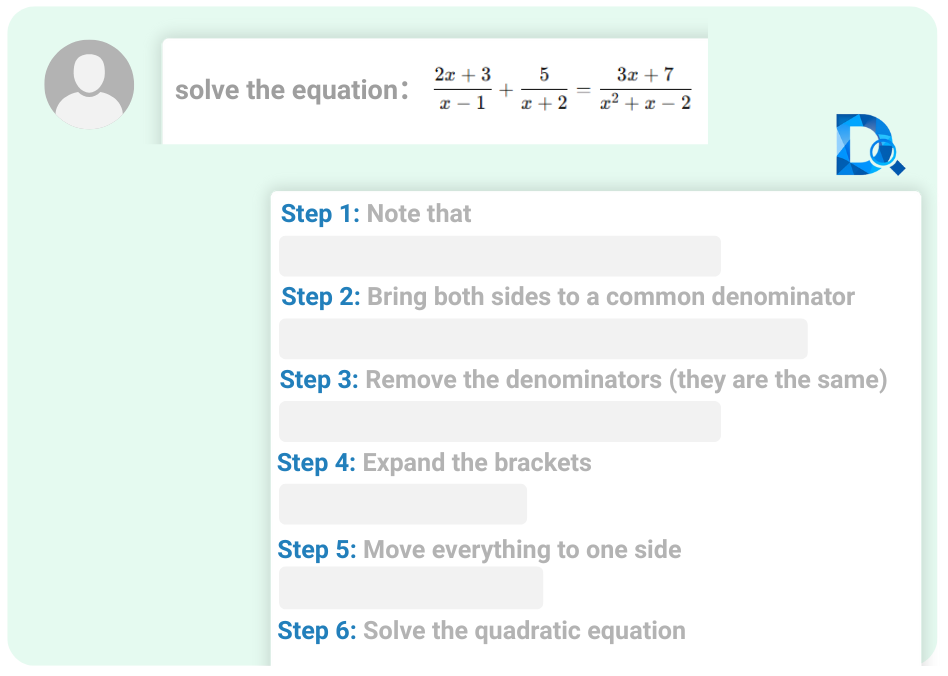
Step-by-Step Solutions
Support for Multiple Equation Types
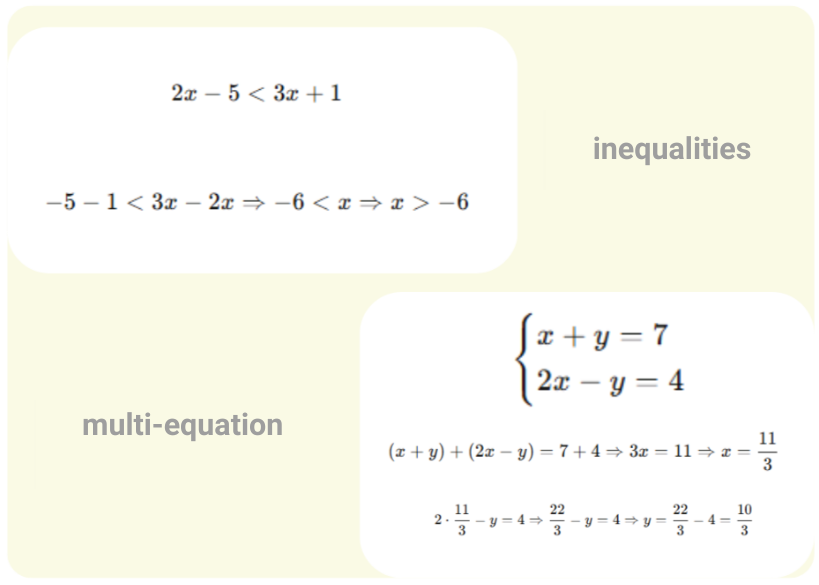
Inequality and System of Equations Solving
Mobile-optimized
A Math Equation Calculator Accessible Anytime,Anywhere
Mobile-friendly online equation calculator supporting photo or manual input with step-by-step analysis.
Student Assignments
Exam Review
Classroom Support
Complex verification
Instructional Grading
Self-Study
Supported Types of Equations
Our equation calculator can solve the following types of math equations. No matter the complexity, you'll get a detailed step-by-step solution.
| Type of Equation | General Form | Solution Features |
|---|---|---|
| Linear equations | ax + b = 0 | One root, solved by rearranging and dividing |
| Quadratic equations | ax² + bx + c = 0 | Quadratic formula, up to two solutions |
| Biquadratic equations | x⁴ + bx² + c = 0 | Solved using variable substitution |
| Polynomial equations | aₙxⁿ + ... + a₀ = 0 | Up to n real or complex roots |
| Logarithmic equations | log_b(f(x)) = g(x) | Solved by rewriting as f(x) = b^g(x) |
| Exponential equations | a^{f(x)} = b^{g(x)} | Logarithmic transformation of both sides |
| Radical equations | √f(x) = g(x) | Square both sides and check domain |
| Absolute value equations | |f(x)| = g(x) | Two cases: f(x)=g(x) and f(x)=–g(x) |
| Trigonometric equations | sin(x), cos(x), ... | Use periodicity and identities |
| Complex equations | f(z) = 0 | Solutions in the complex plane |
| Matrix equations | AX = B | Linear algebra methods, inverse matrices |
| Rational equations | P(x)/Q(x) = 0 | Check domain and find rational roots |
| Floor function equations | ⌊f(x)⌋ = g(x) | Solved within integer intervals |
| Root-based construction | f(x) = (x − r₁)... | Build polynomial from known roots |
| Point-based construction | f(x) through (x₁, y₁)... | Interpolation methods |
| Numerical methods | f(x) = 0 | Approximate root finding (e.g., Newton's method) |
| Differential equations | y', y'' = f(x) | Find function y(x) via solution methods |
How to Use Decopy AI Equation Calculator?
-
1
Open the website and go to equation solver page.
-
2
Upload a photo or directly enter your equation.
-
3
Click "Start Solving" and the system will automatically analyze it.
-
4
View the step-by-step solution or ask follow-up questions.
Who Uses the Online Equation Calculator?
Quickly and accurately solve math equations from elementary to college level, with full support for standardized tests like PSAT, SAT, and state assessments.
Elementary School Students
Used for basic math training to develop early thinking skills in algebra and equations.
Middle and High School Exam Preparation
This tool helps students solve common math equation found in middle and high school exams, including algebra, functions, and trigonometry. Ideal for preparing for assessments like the PSAT, SAT, and state-level math tests.
College Students
Ideal for calculus, advanced mathematics, and linear algebra courses, making it easy to handle complex functions and multivariable equations.
Independent Learners
For adults aiming to develop mathematical thinking and logical structuring. Supports the localized mathematical terminology.
Teachers and tutors
Use this equation solver as a reference for lesson planning, accessing standard solutions and analyzing student responses to improve teaching efficiency.
International students
Covers math sections in postgraduate entrance exams and international standardized tests. Quickly verify answers and save preparation time for equation solving in exams like linear equations, quadratic equations, and systems of equations.
Why Use Our Equation Calculator
100% Free
no sign-up, no ads, and absolutely no hidden costs. Start solving math equations online instantly.
Accurate and Reliable
Powered by an intelligent algorithm, Decopy AI equation solver precisely handles all types of math equations.
Simple and Effective
Even beginners can easily solve math equations using the math equation calculator.
Multilingual Support
This math equation calculator recognizes math equations in 8 different languages, making it suitable for international exams.
No Download Required
Equation calculator works directly in your browser and does not require app installation.
Support for All Types of Equations
Solves core types of equations and systems (linear equations, quadratic equations, trigonometric equations, and more).
What our customers are saying
Frequently Asked Questions (FAQs)
Different types of math equations online require different solving
approaches:
Substitution method – used for solving
systems of equations with two variables;
Elimination method
– applied to remove variables and obtain a particular solution;
Completing the square / root formula
– suitable for solving quadratic equations;
Graphical or numerical methods
– applicable to higher-degree equations or those lacking an
analytical solution;
Equation calculator – ideal for
quickly solving structurally complex or time consuming equations,
while also providing a detailed, step-by-step solution process.
The method of completing the square is a technique for solving
quadratic equations of the form
𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0.
It
involves transforming the expression into a perfect square form,
such as
(𝑥 + 𝑑)² = 𝑒,
which makes the equation easier to
solve visually. This method is particularly useful when solving
quadratic equations where the coefficients are difficult to handle
using standard solving methods.
The most important rule in solving equations online is maintaining
balance between an equation's left and right sides.
Whatever
operation you perform on one side, addition, subtraction,
multiplication, or division—you must do the same on the other side.
Otherwise, the fundamental principle of the equation as an equality
is violated, and the result of solving one equation will be
incorrect.
The steps are as follows:
1. Move terms: Transfer the
unknowns to one side of an equation and the constants to the other
side.
2. Simplify: Combine like terms and simplify the
expression.
3. Solve: Use addition, subtraction,
multiplication, or division to reduce the equation to the form 𝑥 =
value. Always ensure that each operation is applied to both sides of
the equation simultaneously when solving equations online.
Simplifying is a basic operation in solving equations and usually
includes:
1. Removing parentheses;
2. Combining like terms
(e.g., 3x + 2x = 5x);
3. Following the order of operations
(PEMDAS: Parentheses → Exponents → Multiplication/Division →
Addition/Subtraction) to make the math equation cleaner and easier
for solving equations online.
1. Simplify both sides: Combine like terms and expand
parentheses.
2. Isolate the variable: Move all terms
containing the variable to one side.
3. Find the value of the variable:
Use inverse operations to simplify coefficients and find the final
result.
Simply enter a math equation online, this equation solver automatically recognizes variables and structure, using intelligent algorithms (such as algebraic transformations, numerical methods, and others) to solve equations online. It then displays step-by-step solutions with justifications for each stage. This is ideal for learning, checking math homework, or verifying complex examples.
📘 Full List of Supported Math Functions
Explore the syntax and notations you can use in Decopy AI equation calculator.
📂 Click to view supported functions
| Function | Description |
|---|---|
| abs(x) | Absolute value of x |
| arccos(x) | Arccosine of x |
| arccosh(x) | Hyperbolic arccosine |
| arcsin(x) | Arcsine of x |
| arcsinh(x) | Hyperbolic arcsine |
| arctg(x) | Arctangent of x |
| arctgh(x) | Hyperbolic arctangent |
| asec(x) | Arcsecant of x |
| asech(x) | Hyperbolic arcsecant |
| cbrt(x) | Cube root of x |
| ceiling(x) | Round up to nearest integer |
| chi(x) | Hyperbolic cosine integral |
| cos(x) | Cosine of x |
| cosh(x) | Hyperbolic cosine |
| cosec(x), csc(x) | Cosecant of x |
| ctg(x) | Cotangent of x |
| diracdelta(x) | Dirac delta function |
| e | Euler's number ≈ 2.71828 |
| exp(x) | Exponential function (e^x) |
| factorial(x), x! | Factorial of x |
| floor(x) | Round down to nearest integer |
| gamma(x) | Gamma function |
| heaviside(x) | Heaviside step function |
| i | Imaginary unit (√-1) |
| lambertw(x) | Lambert W function |
| ln(x), log(x) | Natural logarithm |
| log(a,x) | Logarithm with base a |
| oo | Infinity |
| pi | Pi ≈ 3.14159 |
| sec(x) | Secant of x |
| sech(x) | Hyperbolic secant |
| sign(x) | Sign of a number |
| sin(x) | Sine of x |
| sinh(x) | Hyperbolic sine |
| sqrt(x) | Square root |
| sqr(x), x^2 | Square of x |
| Si(x), Ci(x), Shi(x), Chi(x) | Integral trigonometric and hyperbolic functions |
| tg(x), tan(x) | Tangent |
| tgh(x) | Hyperbolic tangent |
| x + y, x - y | Addition, subtraction |
| x * y, x / y | Multiplication, division |
| x^n, pow(x,n) | Exponentiation |