Calculadora de Ecuaciones Gratis – Solucionador Paso a Paso
Calculadora de ecuaciones que resuelve ecuaciones lineales, cuadráticas y sistemas de ecuaciones a partir de texto o imagen.


¿Qué es una ecuación?
Una ecuación es una expresión matemática que contiene variables desconocidas. Resolver ecuaciones consiste
en encontrar los valores de esas incógnitas estableciendo una relación entre las cantidades conocidas y
desconocidas. Entre los tipos más comunes se encuentran las ecuaciones de primer grado, ecuaciones de
segundo grado, ecuaciones trigonométricas, ecuaciones logarítmicas y ecuaciones de tercer grado.
Las
ecuaciones son fundamentales en áreas como las matemáticas, la física, la ingeniería y la economía.
Representan herramientas clave para resolver problemas del mundo real y comprender sistemas complejos.
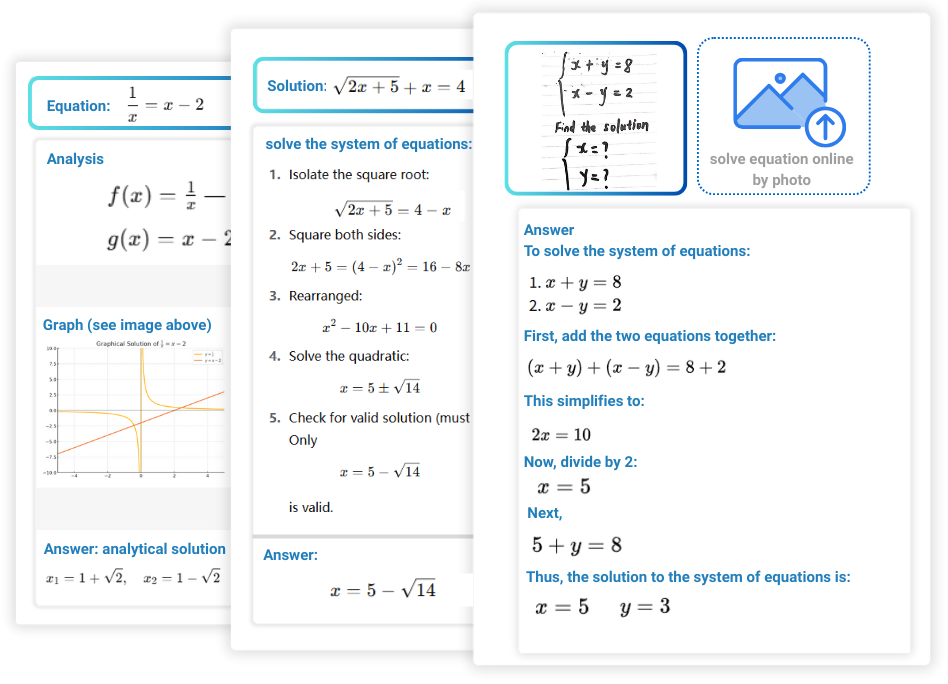
¿Qué es una calculadora de ecuaciones?
Una calculadora de ecuaciones es una herramienta impulsada por inteligencia artificial diseñada para
resolver ecuaciones matemáticas de forma rápida y precisa. Utiliza algoritmos avanzados para analizar la
entrada del usuario y resolver distintos tipos de ecuaciones.
Los usuarios pueden escribir directamente las ecuaciones o subir fotos que las contengan. El resolutor de
ecuaciones reconoce automáticamente el contenido, aplica métodos de resolución estándar y muestra las
soluciones paso a paso.
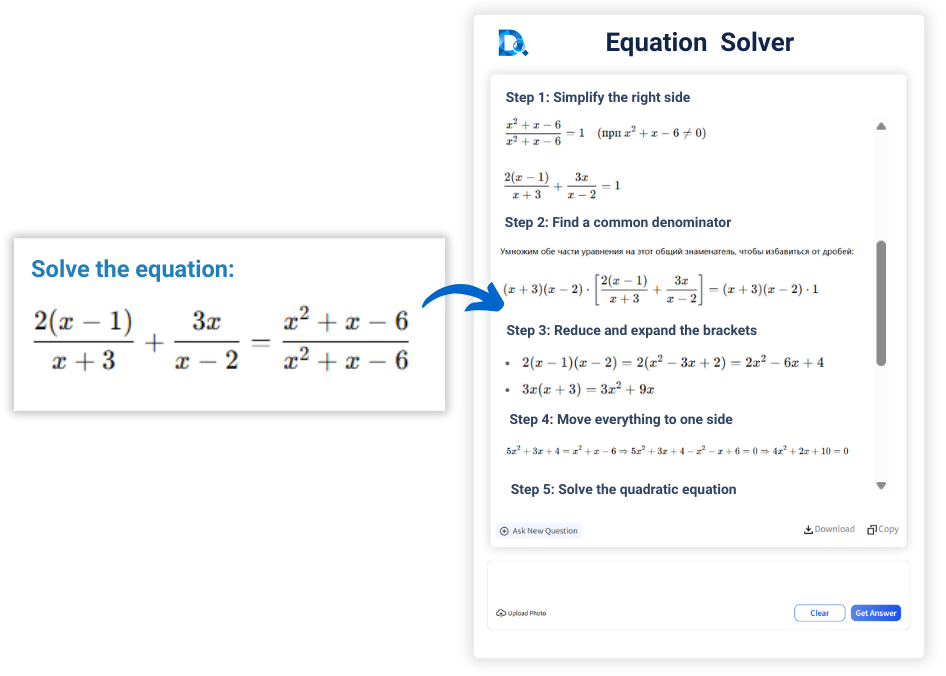
¿Cómo resolver ecuaciones?
Tradicionalmente, resolver ecuaciones implica configurar el problema de forma manual, aplicar
transformaciones y realizar cálculos como factorización, uso del discriminante o eliminación gaussiana.
Para ecuaciones de mayor grado o sistemas no lineales complejos, se requieren métodos matemáticos más
avanzados y técnicas numéricas especializadas.
Con una calculadora de ecuaciones online, puedes
simplemente subir una foto de la fórmula o ingresarla directamente. El resolutor de ecuaciones con
inteligencia artificial proporcionará respuestas precisas en cuestión de segundos. Para facilitar la
comprensión del proceso, la calculadora de ecuaciones simula métodos de resolución utilizados por
humanos—como la eliminación, sustitución o la fórmula cuadrática—y muestra todas las soluciones paso a
paso.

¿Cómo funciona la calculadora de ecuaciones Decopy AI?
La calculadora de ecuaciones Decopy AI está impulsada por un avanzado motor matemático de inteligencia
artificial que integra álgebra, análisis numérico y optimización algorítmica.
Cuando los
usuarios ingresan o cargan ecuaciones matemáticas, el sistema detecta automáticamente el tipo de ecuación
(como ecuaciones de primer grado, ecuaciones de segundo grado, funciones trigonométricas o logarítmicas) y
selecciona el mejor método de resolución según corresponda:
Para ecuaciones lineales y sistemas
de ecuaciones, utiliza eliminación de Gauss o métodos matriciales para una resolución rápida.
Para
ecuaciones cuadráticas, aplica la fórmula general basada en el discriminante con una solución paso a
paso.
Para ecuaciones trigonométricas, logarítmicas y ecuaciones de tercer grado, emplea
transformaciones estándar, factorización o aproximaciones numéricas.
Para sistemas no lineales
complejos, recurre a métodos numéricos o solucionadores avanzados.
Esta calculadora algebraica
online ofrece no solo las respuestas finales, sino también soluciones detalladas paso a paso, ayudando a
los usuarios a comprender los principios matemáticos detrás de cada resultado.

Características de la Calculadora de Ecuaciones
Resuelve ecuaciones matemáticas de forma rápida y precisa en línea mediante fotos o entrada manual. Compatible con todo tipo de ecuaciones y con análisis paso a paso.
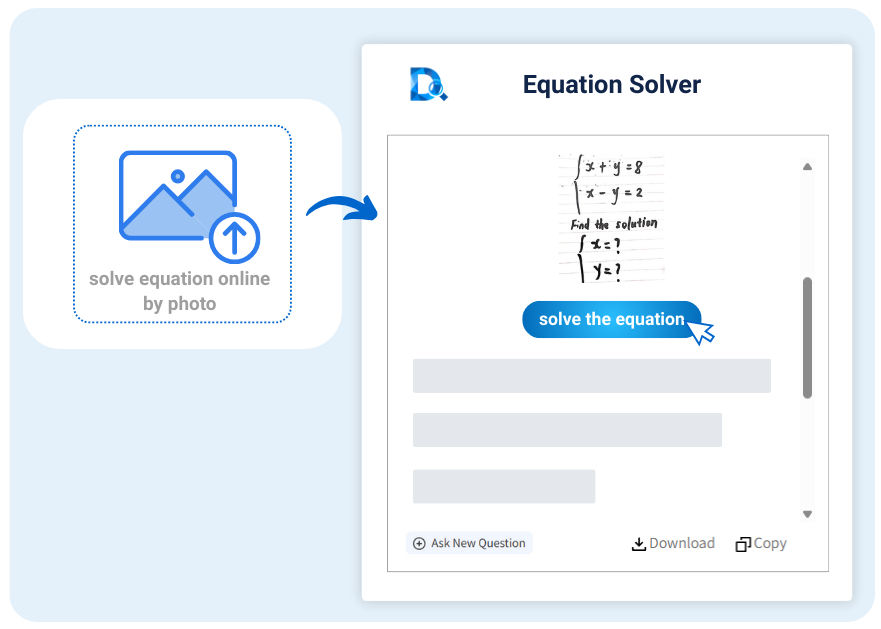
Resolución por foto
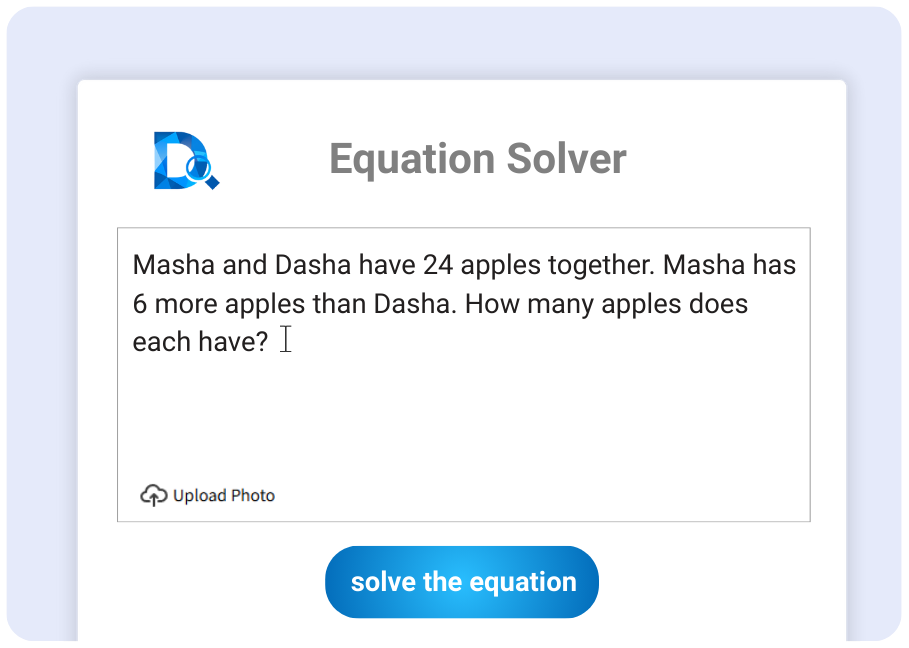
Entrada manual
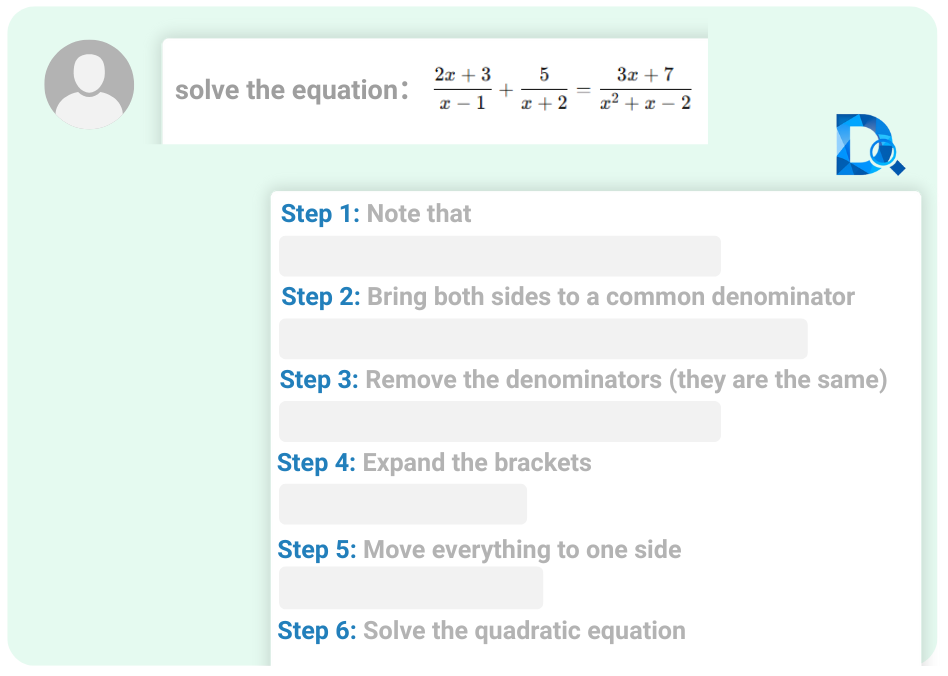
Soluciones paso a paso

Compatibilidad con varios tipos de ecuaciones
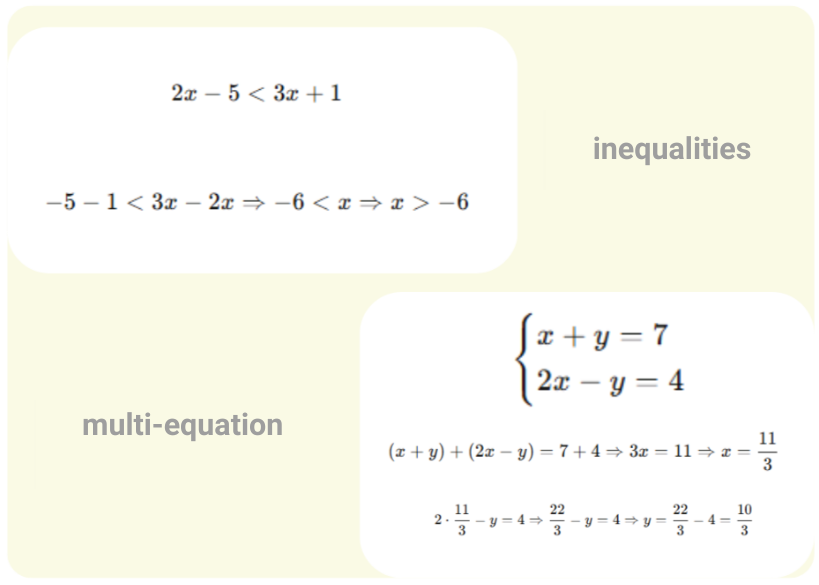
Resolución de desigualdades y sistemas
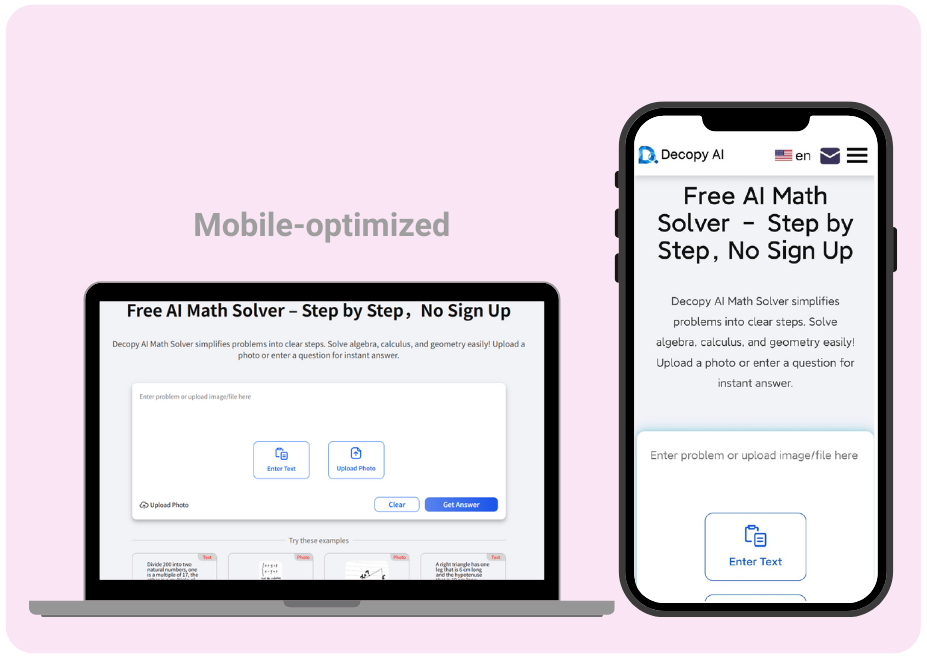
Optimizado para móviles
Calculadora de ecuaciones al instante
Calculadora online compatible con dispositivos móviles para resolver ecuaciones mediante foto o entrada manual, con análisis paso a paso.

Tareas estudiantiles

Revisión para exámenes

Apoyo en el aula

Verificación de ecuaciones complejas

Corrección educativa

Estudio autodidacta
Tipos de Ecuaciones Soportadas
Nuestra calculadora de ecuaciones puede resolver los siguientes tipos de ecuaciones matemáticas. No importa la complejidad, obtendrás una solución detallada paso a paso.
| Tipo de Ecuación | Forma General | Características de la Solución |
|---|---|---|
| Ecuaciones lineales | ax + b = 0 | Una raíz, resuelta mediante reordenamiento y división |
| Ecuaciones cuadráticas | ax² + bx + c = 0 | Fórmula cuadrática, hasta dos soluciones |
| Ecuaciones biquadráticas | x⁴ + bx² + c = 0 | Resuelta usando sustitución de variables |
| Ecuaciones polinomiales | aₙxⁿ + ... + a₀ = 0 | Hasta n raíces reales o complejas |
| Ecuaciones logarítmicas | log_b(f(x)) = g(x) | Resuelta reescribiendo como f(x) = b^g(x) |
| Ecuaciones exponenciales | a^{f(x)} = b^{g(x)} | Transformación logarítmica de ambos lados |
| Ecuaciones radicales | √f(x) = g(x) | Cuadrado ambos lados y verificar dominio |
| Ecuaciones de valor absoluto | |f(x)| = g(x) | Dos casos: f(x)=g(x) y f(x)=–g(x) |
| Ecuaciones trigonométricas | sin(x), cos(x), ... | Usar periodicidad e identidades |
| Ecuaciones complejas | f(z) = 0 | Soluciones en el plano complejo |
| Ecuaciones matriciales | AX = B | Métodos de álgebra lineal, matrices inversas |
| Ecuaciones racionales | P(x)/Q(x) = 0 | Verificar dominio y encontrar raíces racionales |
| Ecuaciones de función de piso | ⌊f(x)⌋ = g(x) | Resuelta dentro de intervalos enteros |
| Construcción basada en raíces | f(x) = (x − r₁)... | Construir polinomio a partir de raíces conocidas |
| Construcción basada en puntos | f(x) a través de (x₁, y₁)... | Métodos de interpolación |
| Métodos numéricos | f(x) = 0 | Encontrar raíz aproximada (por ejemplo, método de Newton) |
| Ecuaciones diferenciales | y', y'' = f(x) | Encontrar la función y(x) mediante métodos de solución |
Cómo utilizar la calculadora de ecuaciones de Decopy AI
- 1
Accede al sitio web y dirígete a la página del solucionador de ecuaciones.
- 2
Sube una foto de tu problema matemático o ingresa la ecuación manualmente.
- 3
Haz clic en “Obtener respuesta” y el sistema analizará automáticamente el problema.
- 4
Consulta la solución detallada o plantea preguntas adicionales.
¿Por qué usar nuestra calculadora de ecuaciones?
100% Gratis
Sin necesidad de registro, sin anuncios y absolutamente sin costos ocultos. Comienza a resolver ecuaciones matemáticas en línea al instante.
Precisa y confiable
Impulsada por un algoritmo inteligente, la calculadora de ecuaciones de Decopy AI maneja con precisión todo tipo de ecuaciones matemáticas.
Simple y efectiva
Incluso los principiantes pueden resolver ecuaciones matemáticas fácilmente usando la calculadora de ecuaciones.
Soporte multilingüe
Esta calculadora de ecuaciones reconoce ecuaciones matemáticas en 8 idiomas diferentes, lo que la hace adecuada para exámenes internacionales.
No requiere descarga
La calculadora de ecuaciones funciona directamente en tu navegador y no requiere instalación de ninguna aplicación.
Soporte para todo tipo de ecuaciones
Resuelve los tipos fundamentales de ecuaciones y sistemas (ecuaciones lineales, ecuaciones cuadráticas, ecuaciones trigonométricas y más).
Lo que nuestros clientes están diciendo
Preguntas Frecuentes (FAQs)
Distintos tipos de ecuaciones matemáticas en línea requieren diferentes enfoques para su resolución:
Método de sustitución
– utilizado para resolver sistemas de ecuaciones con dos variables;
Método de eliminación – se
aplica para eliminar variables y obtener una solución particular;
Completación del cuadrado / fórmula de la raíz
– adecuado para resolver ecuaciones cuadráticas;
Métodos gráficos o numéricos – aplicables a
ecuaciones de grado superior o aquellas que no tienen una solución analítica;
Calculadora de ecuaciones
– ideal para resolver rápidamente ecuaciones estructuralmente complejas o que requieren mucho tiempo,
proporcionando además un proceso detallado de solución paso a paso.
El método de completar el cuadrado es una técnica para resolver ecuaciones cuadráticas de la forma
𝑎𝑥²
+ 𝑏𝑥 + 𝑐 = 0.
Consiste en transformar la expresión en una forma de cuadrado perfecto, como
(𝑥 +
𝑑)² = 𝑒,
lo que hace que la ecuación sea más fácil de resolver visualmente. Este método es
particularmente útil cuando se resuelven ecuaciones cuadráticas cuyos coeficientes son difíciles de manejar
mediante los métodos estándar de resolución.
Para resolver ecuaciones cuadráticas utilizando este
enfoque, se puede recurrir a herramientas como una calculadora de ecuaciones o una calculadora algebraica,
que ayudan a simplificar el proceso.
La regla más importante al resolver ecuaciones en línea es mantener el equilibrio entre los dos lados de la ecuación.Cualquiera que sea la operación que realices en un lado, ya sea suma, resta, multiplicación o división, debes hacer lo mismo en el otro lado. De lo contrario, se viola el principio fundamental de la ecuación como una igualdad, y el resultado de resolver una ecuación será incorrecto.
Resolver una ecuación lineal es un proceso fundamental en álgebra. A continuación, se detallan los pasos
esenciales para encontrar la solución:
1. Mover los términos: Transfiere los términos que
contienen la incógnita a un lado de la ecuación y los términos constantes al otro lado. Este paso es crucial
para simplificar la ecuación.
2. Simplificar: Combina los términos semejantes y simplifica la
expresión. Esto facilita el proceso de resolución y reduce la complejidad de la ecuación.
3. Resolver:
Aplica operaciones de adición, sustracción, multiplicación o división para aislar la incógnita y obtener la
forma x=valorx = ext{valor}x=valor. Es importante recordar que cada operación debe aplicarse simultáneamente
a ambos lados de la ecuación para mantener la igualdad.
Simplificar es una operación básica al resolver ecuaciones y generalmente incluye:
1. Eliminar
paréntesis;
2. Combinar términos semejantes (por ejemplo, 3x + 2x = 5x);
3. Seguir el orden de las
operaciones (PEMDAS: Paréntesis → Exponentes → Multiplicación/División → Suma/Resta) para hacer que la
ecuación matemática sea más clara y fácil de resolver en línea.
1. Simplificar ambos lados: Combina términos semejantes y expande los paréntesis.
2. Aislar la variable:
Mueve todos los términos que contienen la variable a un lado de la ecuación.
3. Encontrar el valor de la variable:
Utiliza operaciones inversas para simplificar los coeficientes y obtener el resultado final.
Simplemente ingresa una ecuación matemática en línea, y este solucionador de ecuaciones reconoce automáticamente las variables y la estructura, utilizando algoritmos inteligentes (como transformaciones algebraicas, métodos numéricos y otros) para resolver ecuaciones en línea. Luego, muestra soluciones paso a paso con justificaciones para cada etapa. Esto es ideal para aprender, revisar tareas de matemáticas o verificar ejemplos complejos.
📘 Lista Completa de Funciones Matemáticas Soportadas
Explora la sintaxis y notaciones que puedes usar en la calculadora de ecuaciones de Decopy AI.
📂 Haz clic para ver las funciones soportadas
| Función | Descripción |
|---|---|
| abs(x) | Valor absoluto de x |
| arccos(x) | Arccoseno de x |
| arccosh(x) | Arccoseno hiperbólico |
| arcsin(x) | Arco seno de x |
| arcsinh(x) | Arco seno hiperbólico |
| arctg(x) | Arco tangente de x |
| arctgh(x) | Arco tangente hiperbólico |
| asec(x) | Arco secante de x |
| asech(x) | Arco secante hiperbólico |
| cbrt(x) | Raíz cúbica de x |
| ceiling(x) | Redondea hacia arriba al entero más cercano |
| chi(x) | Integral coseno hiperbólico |
| cos(x) | Coseno de x |
| cosh(x) | Coseno hiperbólico |
| cosec(x), csc(x) | Cosecante de x |
| ctg(x) | Cotangente de x |
| diracdelta(x) | Función delta de Dirac |
| e | Número de Euler ≈ 2.71828 |
| exp(x) | Función exponencial (e^x) |
| factorial(x), x! | Factorial de x |
| floor(x) | Redondea hacia abajo al entero más cercano |
| gamma(x) | Función gamma |
| heaviside(x) | Función escalón de Heaviside |
| i | Unidad imaginaria (√-1) |
| lambertw(x) | Función W de Lambert |
| ln(x), log(x) | Logaritmo natural |
| log(a,x) | Logaritmo con base a |
| oo | Infinito |
| pi | Pi ≈ 3.14159 |
| sec(x) | Secante de x |
| sech(x) | Secante hiperbólico |
| sign(x) | Signo de un número |
| sin(x) | Senos de x |
| sinh(x) | Senos hiperbólico |
| sqrt(x) | Raíz cuadrada |
| sqr(x), x^2 | Cuadrado de x |
| Si(x), Ci(x), Shi(x), Chi(x) | Funciones trigonométricas e hiperbólicas integrales |
| tg(x), tan(x) | Tangente |
| tgh(x) | Tangente hiperbólica |
| x + y, x - y | Adición, sustracción |
| x * y, x / y | Multiplicación, división |
| x^n, pow(x,n) | Exponenciación |





