Estudiantes
Explora la conexión entre álgebra y geometría, profundiza en la comprensión de conceptos matemáticos y utiliza la calculadora de geometría para completar tareas y proyectos.
Calculadora de geometría que dibuja figuras geométricas y calcula sus propiedades, proporcionando una solución eficiente para el aprendizaje y la exploración de problemas de geometría.
La calculadora de geometría es una potente herramienta que integra funciones de álgebra, geometría y análisis de datos. Está diseñada para el aprendizaje, la enseñanza y la investigación en geometría. La calculadora de geometría en línea ayuda a los usuarios a explorar y resolver problemas geométricos de manera más intuitiva y eficiente.
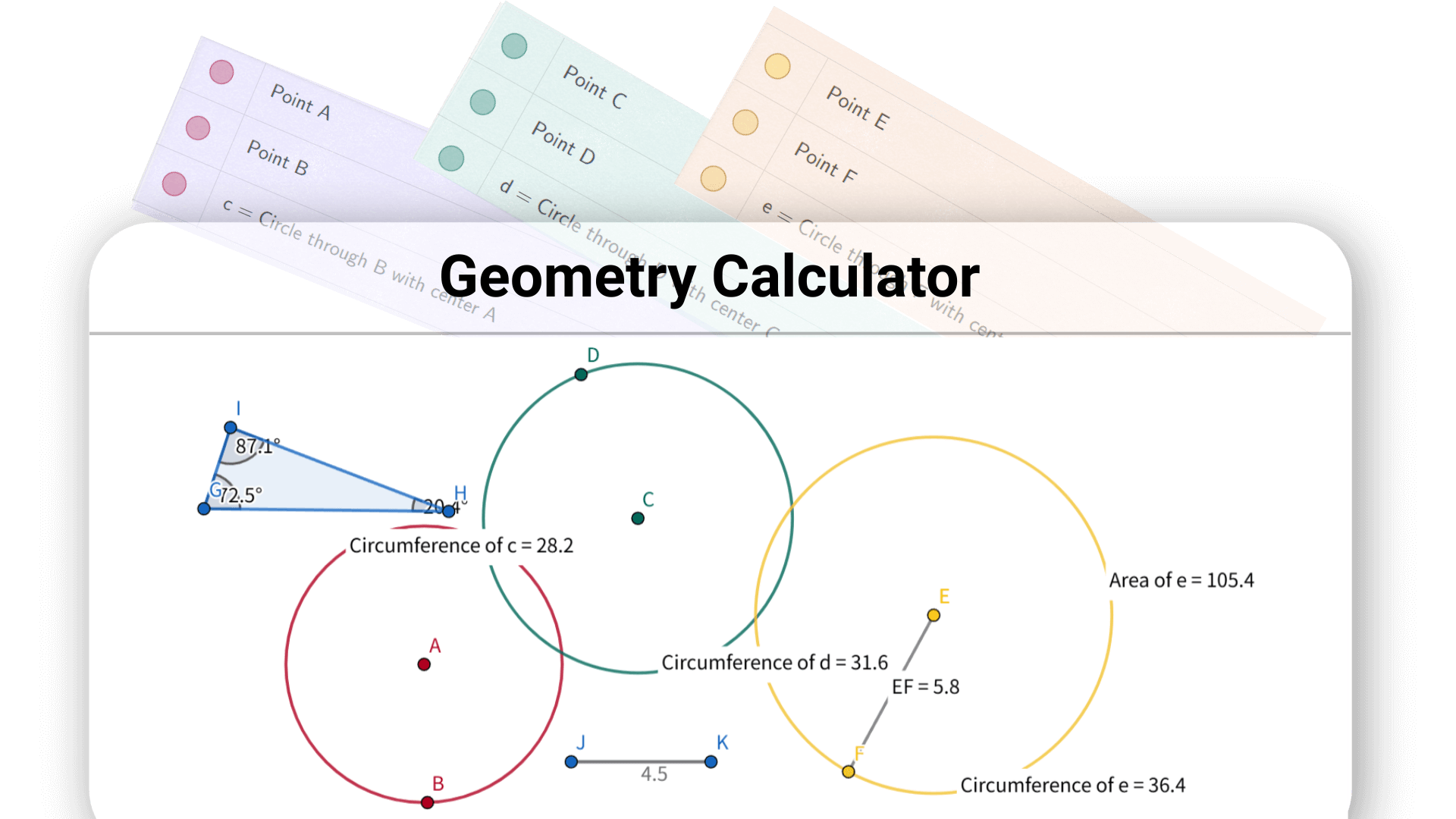
La mejor calculadora de geometría de Decopy puede ahorrarte tiempo valioso, sin necesidad de buscar en libros o dibujar en papel. Te permite centrarte en comprender los conceptos geométricos en lugar de perderte en cálculos complejos.
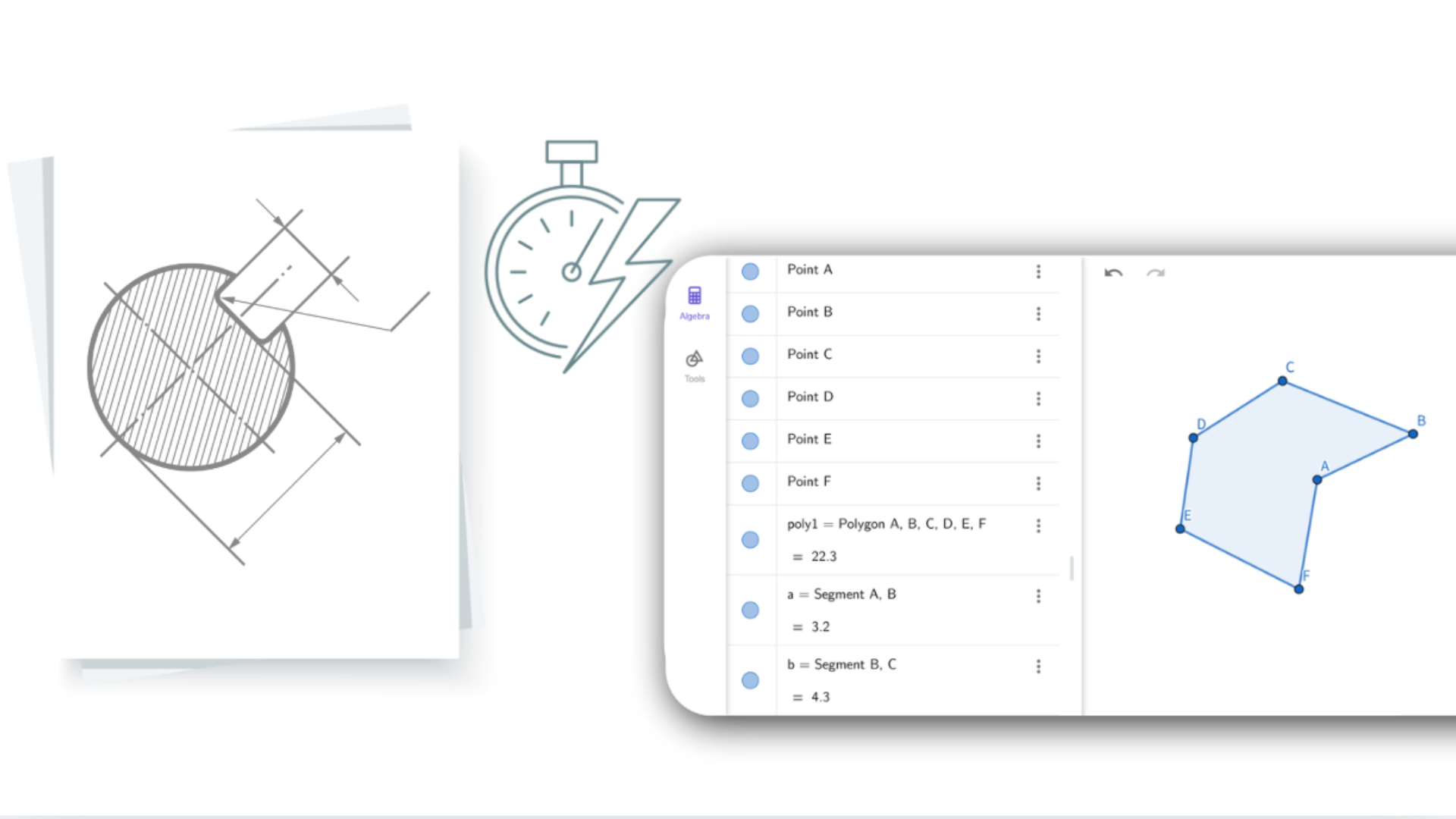
Al ingresar ecuaciones o coordenadas, la calculadora de geometría muestra instantáneamente las formas correspondientes. Al ajustar una figura, se actualizan en tiempo real las expresiones algebraicas relacionadas. Esta interacción dinámica conecta el álgebra con la geometría, ayudando a los usuarios a comprender los problemas desde diferentes perspectivas. La calculadora de geometría hace que las matemáticas abstractas sean visuales y fáciles de entender.
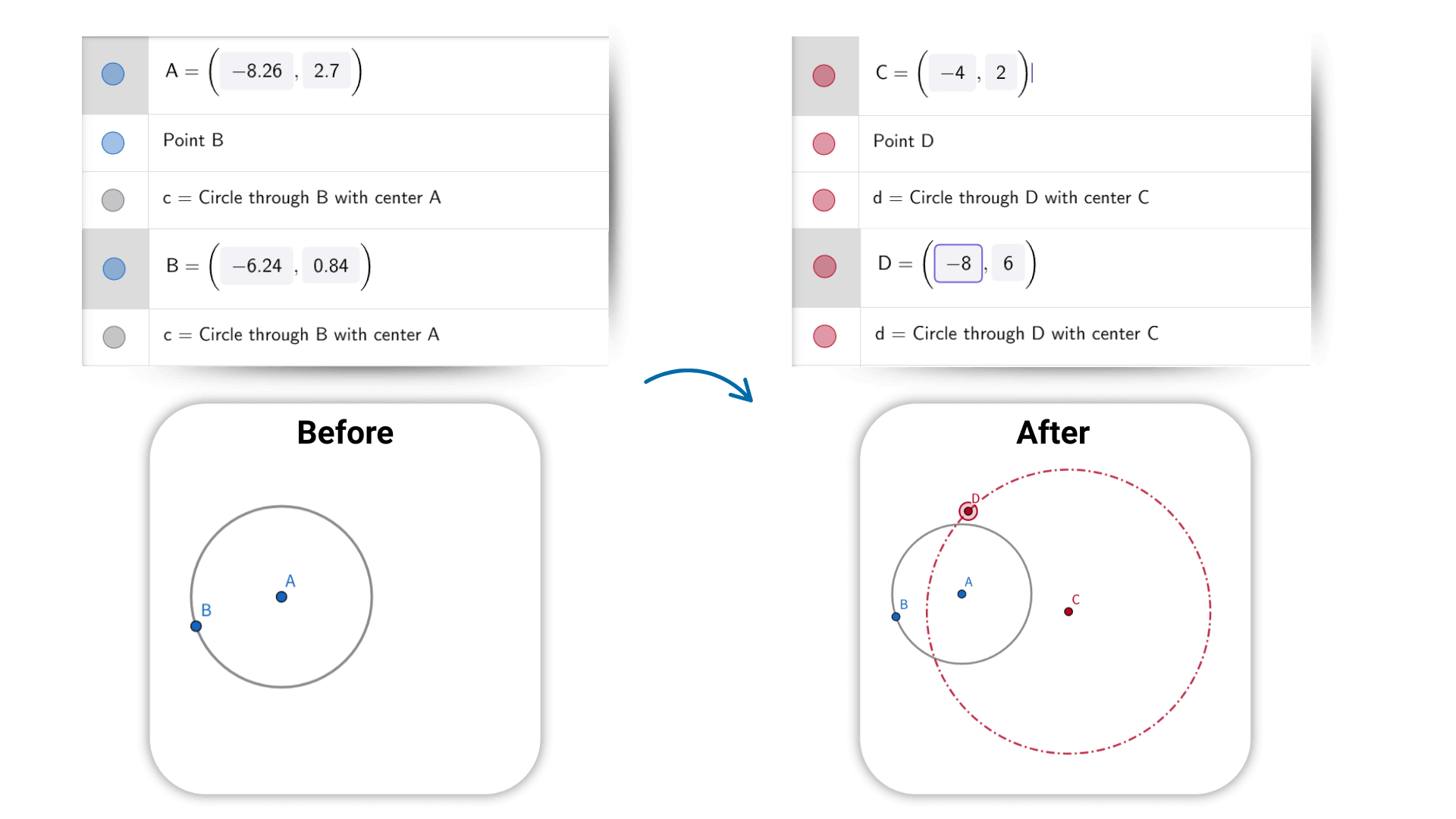
La calculadora de geometría admite transformaciones como traslación, rotación y escalado. Con acciones simples, puedes ver los cambios de las figuras en tiempo real. Las figuras, expresiones y datos son totalmente interactivos: al arrastrar un punto o ajustar un parámetro, se actualizan automáticamente las relaciones y resultados relacionados. Esta calculadora de geometría en línea te ayuda a explorar cómo se conectan y comportan los objetos geométricos, facilitando la comprensión de su naturaleza dinámica.
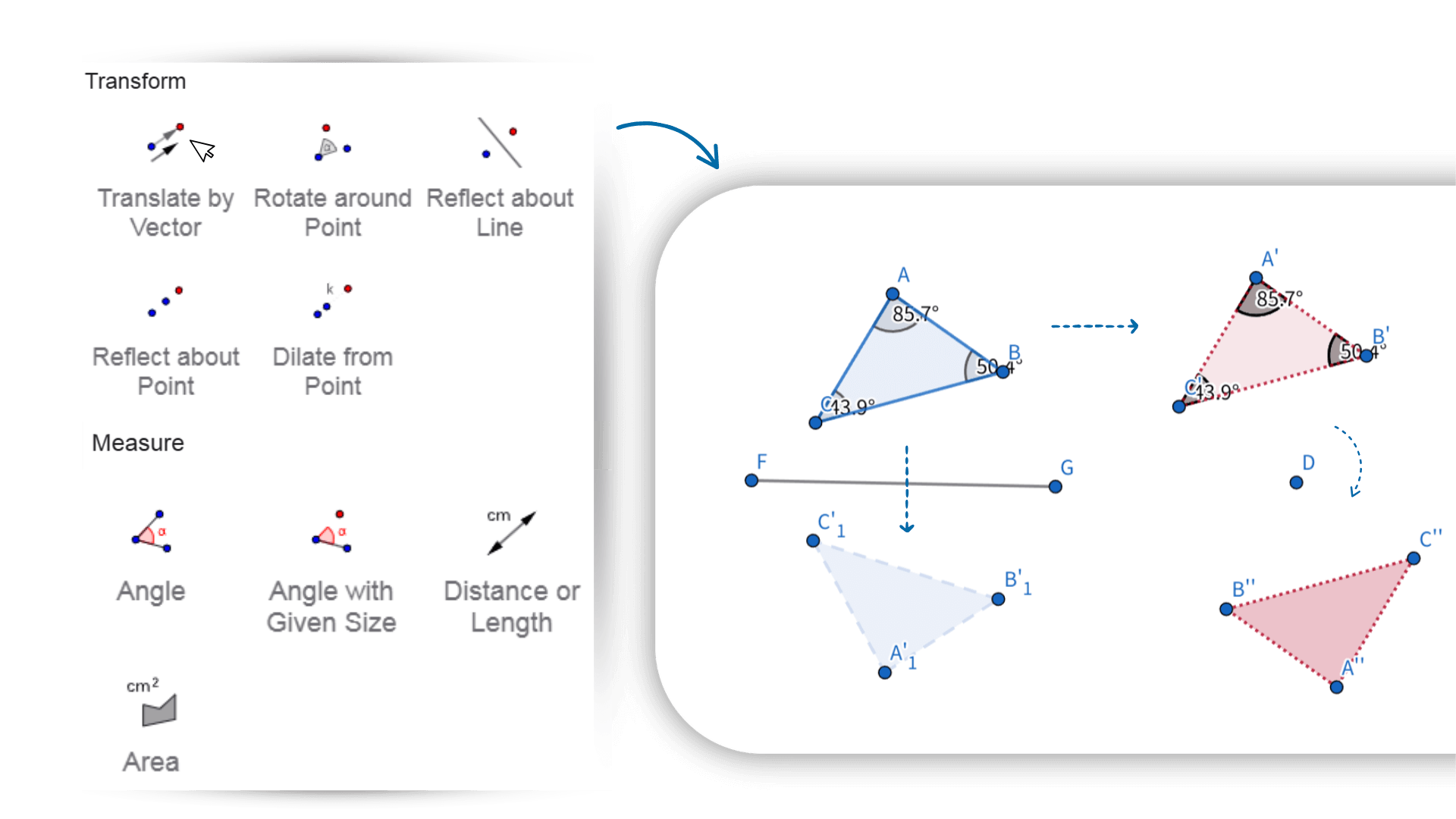
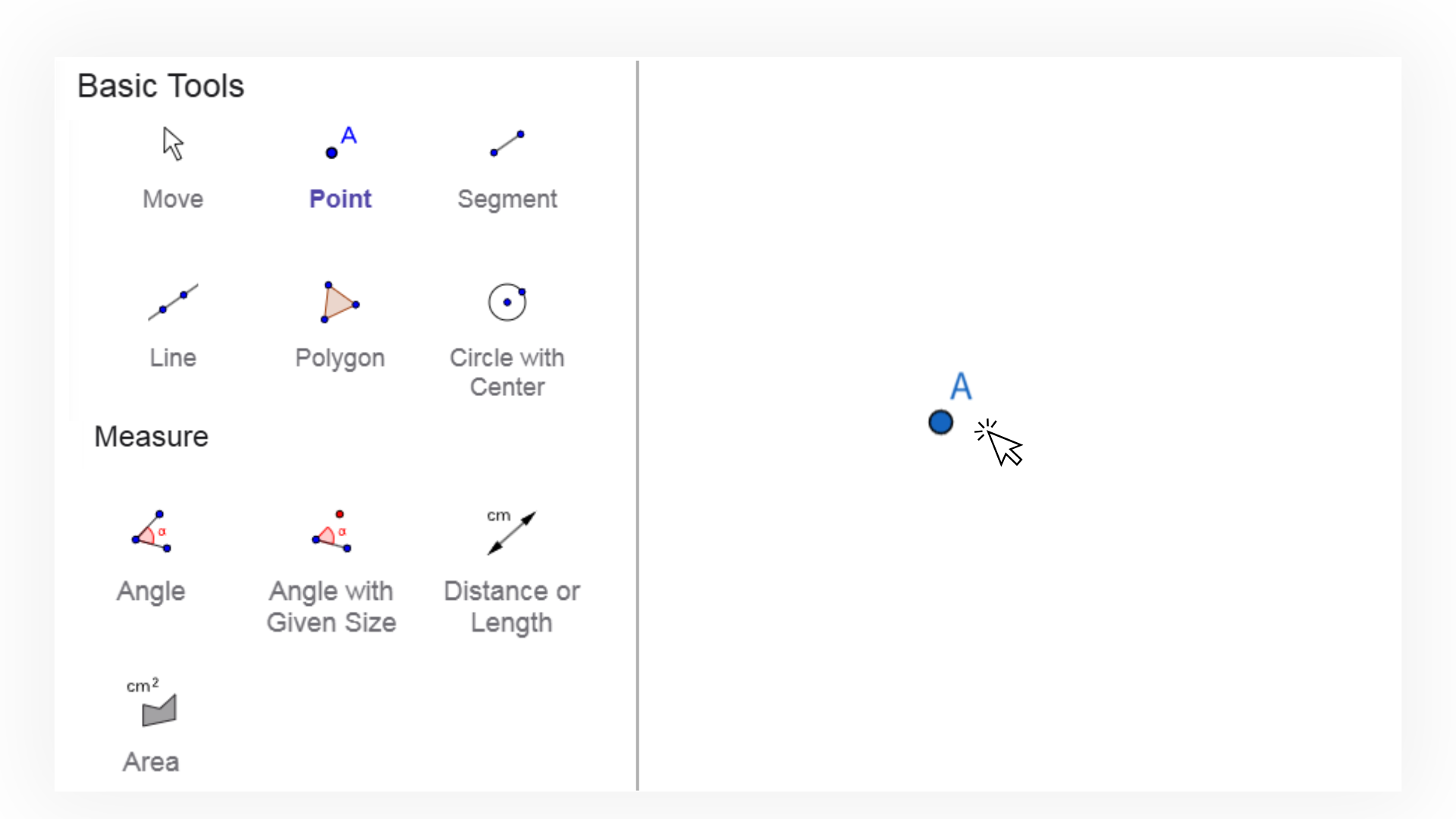
1. ![]() Selecciona la herramienta Línea y crea una línea arbitraria
AB haciendo clic dos veces en la Vista Gráfica.
Selecciona la herramienta Línea y crea una línea arbitraria
AB haciendo clic dos veces en la Vista Gráfica.
2. ![]() Crea una línea BC usando nuevamente la herramienta
Línea.
Crea una línea BC usando nuevamente la herramienta
Línea.
Sugerencia: Selecciona el punto B y luego
haz clic en la Vista Gráfica para crear el punto C.
3. ![]() Activa la herramienta Línea Paralela y crea una línea
paralela a la línea AB que pase por el punto C.
Activa la herramienta Línea Paralela y crea una línea
paralela a la línea AB que pase por el punto C.
Sugerencia:
Abre la Caja de Herramientas de Líneas Especiales, activa la
herramienta Línea Paralela y selecciona la línea AB y luego
el punto C.
4. ![]() Crea una línea paralela a la línea BC que pase por el punto
A usando nuevamente la herramienta Línea Paralela.
Crea una línea paralela a la línea BC que pase por el punto
A usando nuevamente la herramienta Línea Paralela.
5. ![]() Selecciona la herramienta Intersección y crea el punto de
intersección D de las dos líneas.
Selecciona la herramienta Intersección y crea el punto de
intersección D de las dos líneas.
Sugerencia:
Abre la Caja de Herramientas de Puntos, activa la
herramienta Intersección y haz clic directamente en el punto
de intersección.
6. ![]() Activa la herramienta Polígono y crea el paralelogramo ABCD
seleccionando sucesivamente todos los vértices.
Activa la herramienta Polígono y crea el paralelogramo ABCD
seleccionando sucesivamente todos los vértices.
Nota:
Para cerrar el polígono, selecciona nuevamente el primer
punto.
7. ![]() Selecciona la herramienta Mover y arrastra los vértices del
paralelogramo para comprobar si fue construido
correctamente.
Selecciona la herramienta Mover y arrastra los vértices del
paralelogramo para comprobar si fue construido
correctamente.
1. ![]() Crea el segmento AB haciendo clic dos veces en la Vista
Gráfica.
Crea el segmento AB haciendo clic dos veces en la Vista
Gráfica.
2. ![]() Construye un círculo con centro en B y que pase por A
seleccionando ambos puntos en ese orden.
Construye un círculo con centro en B y que pase por A
seleccionando ambos puntos en ese orden.
3. ![]() Arrastra los puntos A y B para comprobar si el círculo está
conectado a ellos.
Arrastra los puntos A y B para comprobar si el círculo está
conectado a ellos.
4. ![]() Construye un círculo con centro en B y que pase por A
seleccionando ambos puntos en ese orden.
Construye un círculo con centro en B y que pase por A
seleccionando ambos puntos en ese orden.
5. ![]() Interseca ambos círculos seleccionándolos para obtener el
punto C.
Interseca ambos círculos seleccionándolos para obtener el
punto C.
6. ![]() Crea el polígono ABC en sentido antihorario. Para cerrar el
polígono selecciona nuevamente el primer punto.
Crea el polígono ABC en sentido antihorario. Para cerrar el
polígono selecciona nuevamente el primer punto.
7. ![]() Oculta los dos círculos activando la herramienta
Mostrar/Ocultar Objeto y seleccionándolos. Confirma tu
selección seleccionando la herramienta Mover.
Oculta los dos círculos activando la herramienta
Mostrar/Ocultar Objeto y seleccionándolos. Confirma tu
selección seleccionando la herramienta Mover.
8. ![]() Muestra los ángulos interiores del triángulo haciendo clic
dentro del triángulo.
Muestra los ángulos interiores del triángulo haciendo clic
dentro del triángulo.
Sugerencia: Si obtienes los ángulos exteriores,
probablemente creaste el polígono en sentido horario.
9. ![]() Aplica la Prueba de Arrastre para comprobar si la
construcción es correcta.
Aplica la Prueba de Arrastre para comprobar si la
construcción es correcta.
1. ![]() Crea un triángulo arbitrario ABC haciendo clic tres veces
en la Vista Gráfica y luego seleccionando nuevamente el
primer punto creado.
Crea un triángulo arbitrario ABC haciendo clic tres veces
en la Vista Gráfica y luego seleccionando nuevamente el
primer punto creado.
2. ![]() Construye la mediatriz de cada lado del triángulo.
Construye la mediatriz de cada lado del triángulo.
Sugerencia:
La herramienta Mediatriz se puede aplicar a un segmento
existente.
3. ![]() Crea el punto de intersección D de dos de las
mediatrices.
Crea el punto de intersección D de dos de las
mediatrices.
Sugerencia: La herramienta
Intersección se puede aplicar a la intersección de tres
líneas o seleccionando sucesivamente dos de las tres
mediatrices.
4. ![]() Construye un círculo con centro en D y que pase por uno de
los vértices del triángulo ABC seleccionando primero D y
luego uno de los vértices.
Construye un círculo con centro en D y que pase por uno de
los vértices del triángulo ABC seleccionando primero D y
luego uno de los vértices.
5. ![]() Realiza la Prueba de Arrastre moviendo los vértices del
triángulo para comprobar si tu construcción es
correcta.
Realiza la Prueba de Arrastre moviendo los vértices del
triángulo para comprobar si tu construcción es
correcta.
1. ![]() Asegúrate de tener la imagen de la flor amarilla guardada
en tu computadora antes de comenzar la construcción.
Asegúrate de tener la imagen de la flor amarilla guardada
en tu computadora antes de comenzar la construcción.
2. ![]() Crea un nuevo punto A.
Crea un nuevo punto A.
3. ![]() Construye una línea de reflexión a través de dos nuevos
puntos haciendo clic dos veces en la Vista Gráfica.
Construye una línea de reflexión a través de dos nuevos
puntos haciendo clic dos veces en la Vista Gráfica.
4. ![]() Refleja el punto A en la línea para obtener su imagen
A’.
Refleja el punto A en la línea para obtener su imagen
A’.
Sugerencia: Primero selecciona el punto A y
luego la línea.
5. ![]() Crea un segmento entre el punto A y su imagen A’
seleccionando ambos puntos.
Crea un segmento entre el punto A y su imagen A’
seleccionando ambos puntos.
6. ![]() Activa el rastro para los puntos A y A′.
Activa el rastro para los puntos A y A′.
Sugerencia:
Haz clic derecho (MacOS: Ctrl-clic) en un punto y selecciona
Mostrar Rastro.
Nota: Cada vez que se mueva el
punto A, dejará un rastro en la Vista Gráfica.
7. ![]() Arrastra el punto A para dibujar un rastro.
Arrastra el punto A para dibujar un rastro.
Sugerencia:
El elemento de menú Refrescar Vistas en el menú Vista borra
todos los rastros.
1. ![]() Asegúrate de tener la imagen del atardecer guardada en tu
computadora antes de comenzar la construcción.
Asegúrate de tener la imagen del atardecer guardada en tu
computadora antes de comenzar la construcción.
2. ![]() Inserta la imagen del atardecer en la parte izquierda de la
Vista Gráfica usando la herramienta Imagen.
Inserta la imagen del atardecer en la parte izquierda de la
Vista Gráfica usando la herramienta Imagen.
Nota: El primer punto de esquina A y el segundo punto
de esquina B de la imagen se crean automáticamente.
3. ![]() Mueve el punto A en la esquina inferior izquierda de la
imagen y observa cómo esto afecta la imagen.
Mueve el punto A en la esquina inferior izquierda de la
imagen y observa cómo esto afecta la imagen.
4. ![]() Elimina el punto B usando la herramienta Borrar.
Elimina el punto B usando la herramienta Borrar.
5. ![]() Crea un nuevo punto B ingresando B = A + (3, 0) en la Barra
de Entrada.
Crea un nuevo punto B ingresando B = A + (3, 0) en la Barra
de Entrada.
Sugerencia: No olvides presionar
Enter después de tu entrada.
6. ![]() Configura el nuevo punto B como el SEGUNDO punto de esquina
de la imagen para cambiar su ancho a 3 cm.
Configura el nuevo punto B como el SEGUNDO punto de esquina
de la imagen para cambiar su ancho a 3 cm.
Sugerencia: Abre la Configuración de la imagen y
selecciona la pestaña Posición.
7. ![]() Crea una línea vertical a través de dos puntos en el centro
de la Vista Gráfica usando la herramienta Línea.
Crea una línea vertical a través de dos puntos en el centro
de la Vista Gráfica usando la herramienta Línea.
8. ![]() Refleja la imagen en la línea usando la herramienta
Reflejar respecto a una línea seleccionando la imagen y
luego la línea.
Refleja la imagen en la línea usando la herramienta
Reflejar respecto a una línea seleccionando la imagen y
luego la línea.
9. ![]() Quizás quieras reducir la opacidad de la imagen para
distinguirla mejor del original (Configuración de la imagen,
pestaña Color).
Quizás quieras reducir la opacidad de la imagen para
distinguirla mejor del original (Configuración de la imagen,
pestaña Color).
1. ![]() Asegúrate de tener la imagen de Bart Simpson guardada en tu
computadora antes de comenzar la construcción.
Asegúrate de tener la imagen de Bart Simpson guardada en tu
computadora antes de comenzar la construcción.
2. ![]() Selecciona la herramienta Imagen para insertar la imagen de
Bart.
Selecciona la herramienta Imagen para insertar la imagen de
Bart.
Sugerencia: La Calculadora de Geometría
creará automáticamente el primer y segundo punto de esquina
A y B de la imagen.
3. ![]() Arrastra el primer punto de esquina A de la imagen a la
posición (1, 1).
Arrastra el primer punto de esquina A de la imagen a la
posición (1, 1).
4. ![]() Crea el punto D = (1, 3.9).
Crea el punto D = (1, 3.9).
Sugerencia: Puedes
ingresar las coordenadas directamente en la Barra de
Entrada.
5. ![]() Configura el punto D como el CUARTO punto de esquina de la
imagen.
Configura el punto D como el CUARTO punto de esquina de la
imagen.
Sugerencia: Abre la Configuración de la
imagen y selecciona la pestaña Posición.
6. ![]() Crea un triángulo rígido ABD usando la herramienta Polígono
Rígido.
Crea un triángulo rígido ABD usando la herramienta Polígono
Rígido.
Sugerencia: Cierra el polígono
seleccionando nuevamente el primer punto. El polígono
resultante mantendrá su forma al moverlo. Puede moverse o
rotarse arrastrando dos vértices.
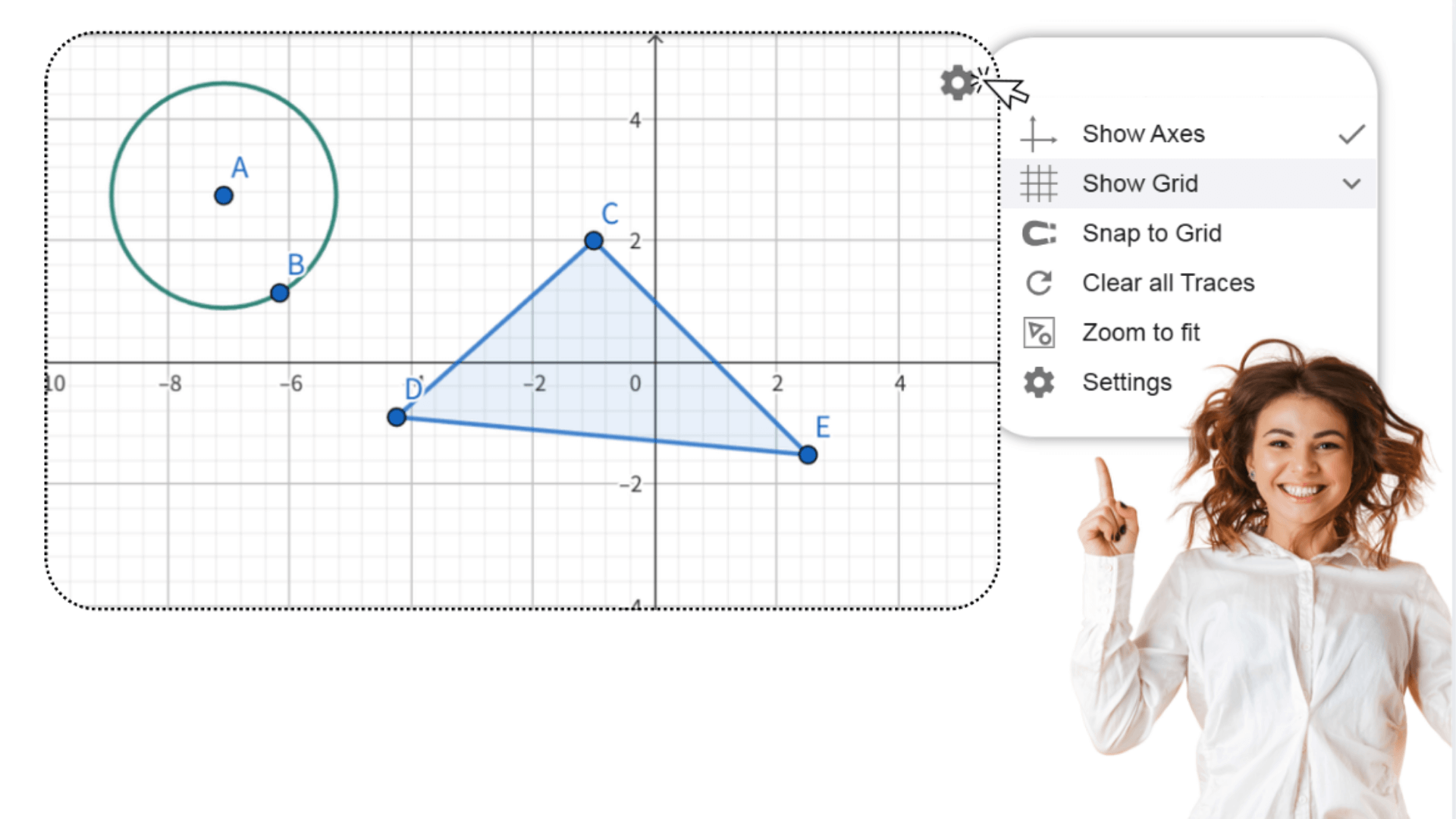
1. ![]() Crea un triángulo arbitrario ABC en el primer cuadrante,
colocando los vértices en puntos de la cuadrícula.
Crea un triángulo arbitrario ABC en el primer cuadrante,
colocando los vértices en puntos de la cuadrícula.
2. ![]() Crea un nuevo punto D en el origen del sistema de
coordenadas.
Crea un nuevo punto D en el origen del sistema de
coordenadas.
3. ![]() Renombra el punto D como O.
Renombra el punto D como O.
Sugerencia:
Selecciona el punto D y simplemente escribe O para abrir el
diálogo de renombrar.
4. ![]() Crea un deslizador para el ángulo α.
Crea un deslizador para el ángulo α.
Sugerencia:
En la ventana de diálogo del deslizador, marca Ángulo y
establece el incremento en 90°. Asegúrate de no borrar el
símbolo °.
5. ![]() Utiliza la herramienta Rotar alrededor de un Punto para
rotar el triángulo ABC alrededor del punto O por el ángulo
α.
Utiliza la herramienta Rotar alrededor de un Punto para
rotar el triángulo ABC alrededor del punto O por el ángulo
α.
Sugerencias: Activa la herramienta y
selecciona el triángulo antes de seleccionar el centro de
rotación. En el diálogo que aparece, ingresa α como el
ángulo usando el Teclado Virtual y elige rotación
antihoraria.
6. ![]() Crea los segmentos AO y A’O.
Crea los segmentos AO y A’O.
7. ![]() Crea el ángulo AOA’.
Crea el ángulo AOA’.
Sugerencia: Selecciona los
puntos en sentido antihorario.
8. ![]() Oculta la etiqueta del ángulo AOA’.
Oculta la etiqueta del ángulo AOA’.
9. ![]() Mueve el deslizador y explora la imagen del
triángulo.
Mueve el deslizador y explora la imagen del
triángulo.
1. ![]() Crea deslizadores a, b y c para las longitudes de los lados
del triángulo con un intervalo de 0 a 10 y un incremento de
0.5 cada uno.
Crea deslizadores a, b y c para las longitudes de los lados
del triángulo con un intervalo de 0 a 10 y un incremento de
0.5 cada uno.
2. ![]() Establece los valores de los deslizadores en a = 8, b = 6.5
y c = 10.
Establece los valores de los deslizadores en a = 8, b = 6.5
y c = 10.
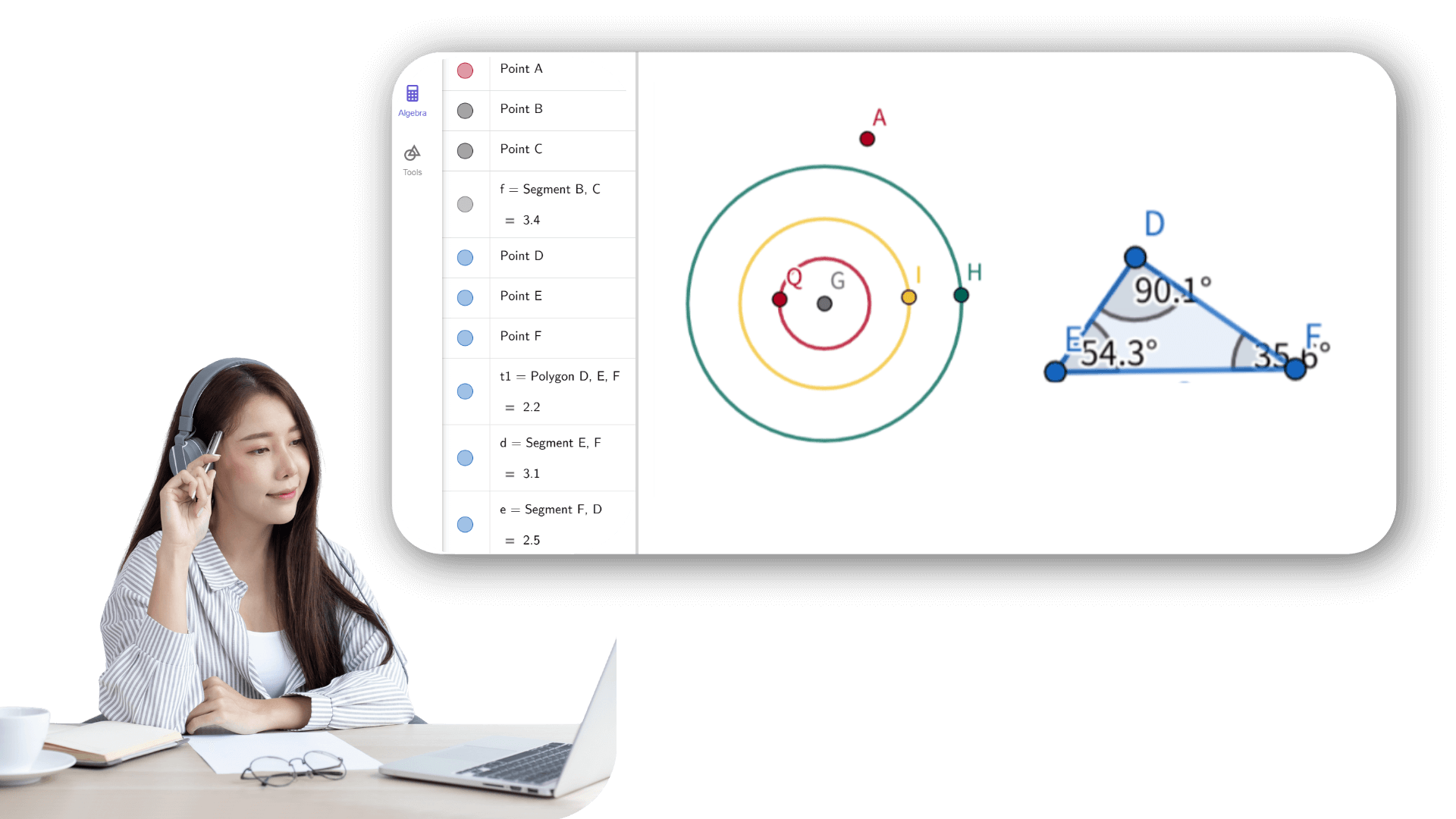
3. ![]() Crea el segmento f con longitud c dada.
Crea el segmento f con longitud c dada.
Sugerencia:
Los puntos A y B son los extremos del segmento.
4. ![]() Crea un círculo d con centro en A y radio b.
Crea un círculo d con centro en A y radio b.
5. ![]() Crea un círculo e con centro en B y radio a.
Crea un círculo e con centro en B y radio a.
6. ![]() Construye el punto de intersección C de los dos círculos e
y f.
Construye el punto de intersección C de los dos círculos e
y f.
7. ![]() Crea el triángulo ABC.
Crea el triángulo ABC.
8. ![]() Crea los ángulos interiores α, β y γ del triángulo
ABC.
Crea los ángulos interiores α, β y γ del triángulo
ABC.
9. ![]() Crea un punto D sobre el círculo d.
Crea un punto D sobre el círculo d.
10. ![]() Crea el segmento g entre los puntos A y D.
Crea el segmento g entre los puntos A y D.
11. ![]() Construye el punto medio E del segmento g.
Construye el punto medio E del segmento g.
12. ![]() Introduce el texto1: b y asígnalo al punto E.
Introduce el texto1: b y asígnalo al punto E.
Sugerencia:
Después de seleccionar la herramienta Texto, haz clic en el
punto E. Abre Avanzado y selecciona b en la pestaña de
Objetos.
13. ![]() Crea un punto F sobre el círculo e.
Crea un punto F sobre el círculo e.
14. ![]() Crea el segmento h entre los puntos B y F.
Crea el segmento h entre los puntos B y F.
15. ![]() Construye el punto medio G del segmento h.
Construye el punto medio G del segmento h.
16. ![]() Introduce el texto2: a y asígnalo al punto G.
Introduce el texto2: a y asígnalo al punto G.
17. ![]() Oculta los puntos D, E, F y G usando la herramienta
Mostrar/Ocultar Objeto.
Oculta los puntos D, E, F y G usando la herramienta
Mostrar/Ocultar Objeto.
18. ![]() Mejora tu construcción usando la Barra de Estilo y combina
los colores de los objetos correspondientes.
Mejora tu construcción usando la Barra de Estilo y combina
los colores de los objetos correspondientes.
1. ![]() Crea un triángulo ABC con orientación antihoraria.
Crea un triángulo ABC con orientación antihoraria.
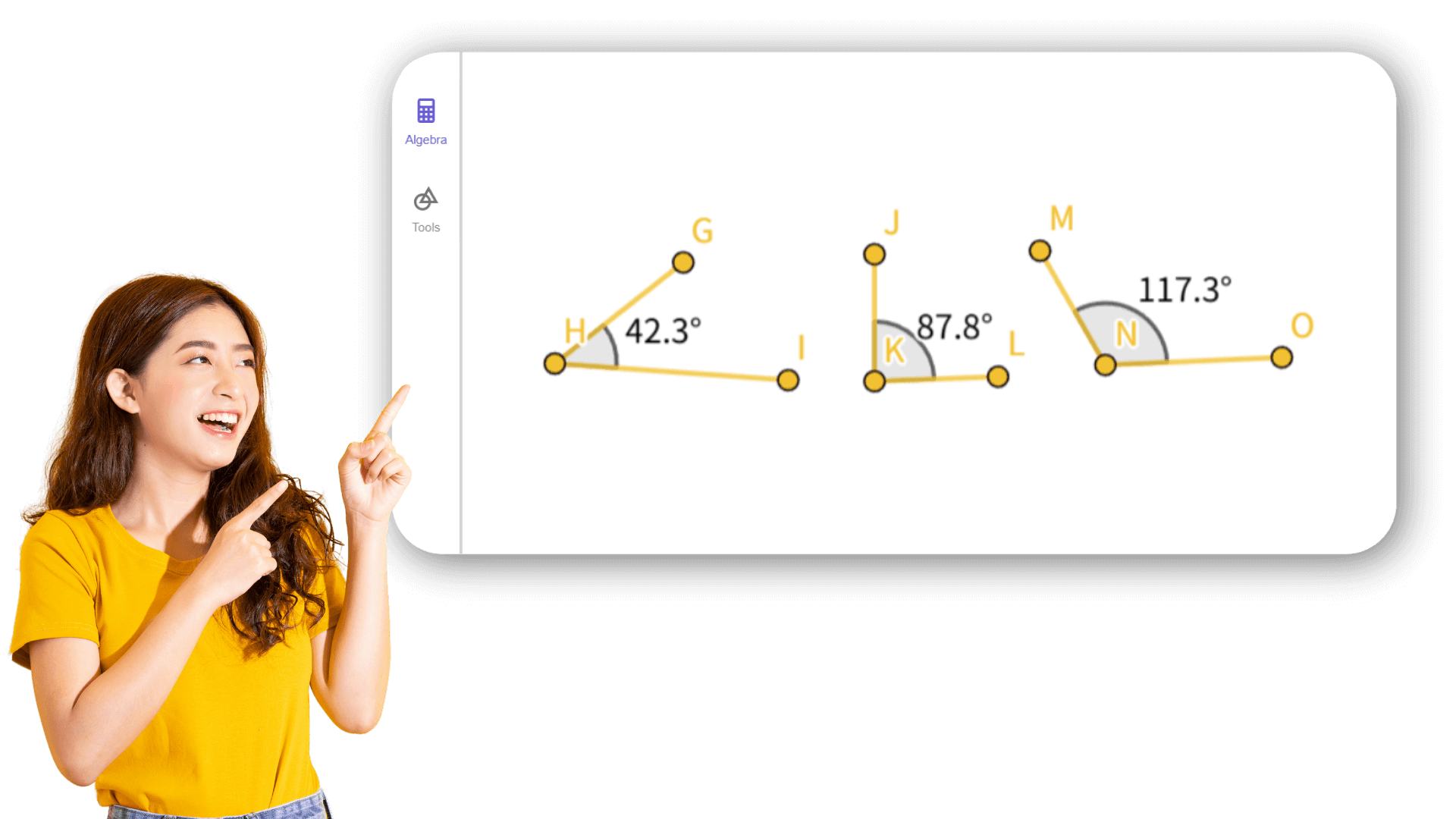
2. ![]() Crea los ángulos α, β y γ del triángulo ABC.
Crea los ángulos α, β y γ del triángulo ABC.
3. ![]() Crea un deslizador para el ángulo δ con intervalo de 0° a
180° e incremento de 10°.
Crea un deslizador para el ángulo δ con intervalo de 0° a
180° e incremento de 10°.
4. ![]() Crea un deslizador para el ángulo ε con intervalo de 0° a
180° e incremento de 10°.
Crea un deslizador para el ángulo ε con intervalo de 0° a
180° e incremento de 10°.
5. ![]() Crea el punto medio D del segmento AC y el punto medio E
del segmento AB.
Crea el punto medio D del segmento AC y el punto medio E
del segmento AB.
6. ![]() Rota el triángulo alrededor del punto D por el ángulo δ
(configuración en sentido horario).
Rota el triángulo alrededor del punto D por el ángulo δ
(configuración en sentido horario).
Sugerencia:
Ingresa δ usando el Teclado Virtual.
7. ![]() Rota el triángulo alrededor del punto E por el ángulo ε
(configuración en sentido antihorario).
Rota el triángulo alrededor del punto E por el ángulo ε
(configuración en sentido antihorario).
Sugerencia:
Ingresa ε usando el Teclado Virtual.
8. ![]() Mueve ambos deslizadores δ y ε para mostrar 180°.
Mueve ambos deslizadores δ y ε para mostrar 180°.
9. ![]() Crea el ángulo ζ usando los puntos A’C’B’.
Crea el ángulo ζ usando los puntos A’C’B’.
Sugerencia:
Para asegurarte de seleccionar los vértices correctos,
cambia el ángulo δ o usa el comando
angle(A’, C’, B’).
10. ![]() Crea el ángulo η usando los puntos C'1B'1A'1.
Crea el ángulo η usando los puntos C'1B'1A'1.
Sugerencia:
Para asegurarte de seleccionar los vértices correctos,
cambia el ángulo ε antes o usa el comando
angle(C'1, B'1, A'1).
11. ![]() Mejora tu construcción usando la Barra de Estilo.
Mejora tu construcción usando la Barra de Estilo.
Sugerencia:
Los ángulos congruentes deben tener el mismo color.
12. ![]() Crea un texto dinámico mostrando los ángulos interiores y
sus valores (por ejemplo, ingresa α = y selecciona α de la
lista de objetos en la pestaña Avanzado).
Crea un texto dinámico mostrando los ángulos interiores y
sus valores (por ejemplo, ingresa α = y selecciona α de la
lista de objetos en la pestaña Avanzado).
13. ![]() Calcula la suma de los ángulos ingresando
Calcula la suma de los ángulos ingresando
suma = α + β + γ en la Barra de Entrada.
14. ![]() Inserta la suma de los ángulos como texto dinámico:
Inserta la suma de los ángulos como texto dinámico:
α + β + γ = y selecciona suma de la lista de
objetos en la pestaña.
15. ![]() Combina los colores de los ángulos y textos
correspondientes usando la Barra de Estilo.
Combina los colores de los ángulos y textos
correspondientes usando la Barra de Estilo.
16. ![]() Fija todos los textos que no deban moverse usando la Barra
de Estilo.
Fija todos los textos que no deban moverse usando la Barra
de Estilo.
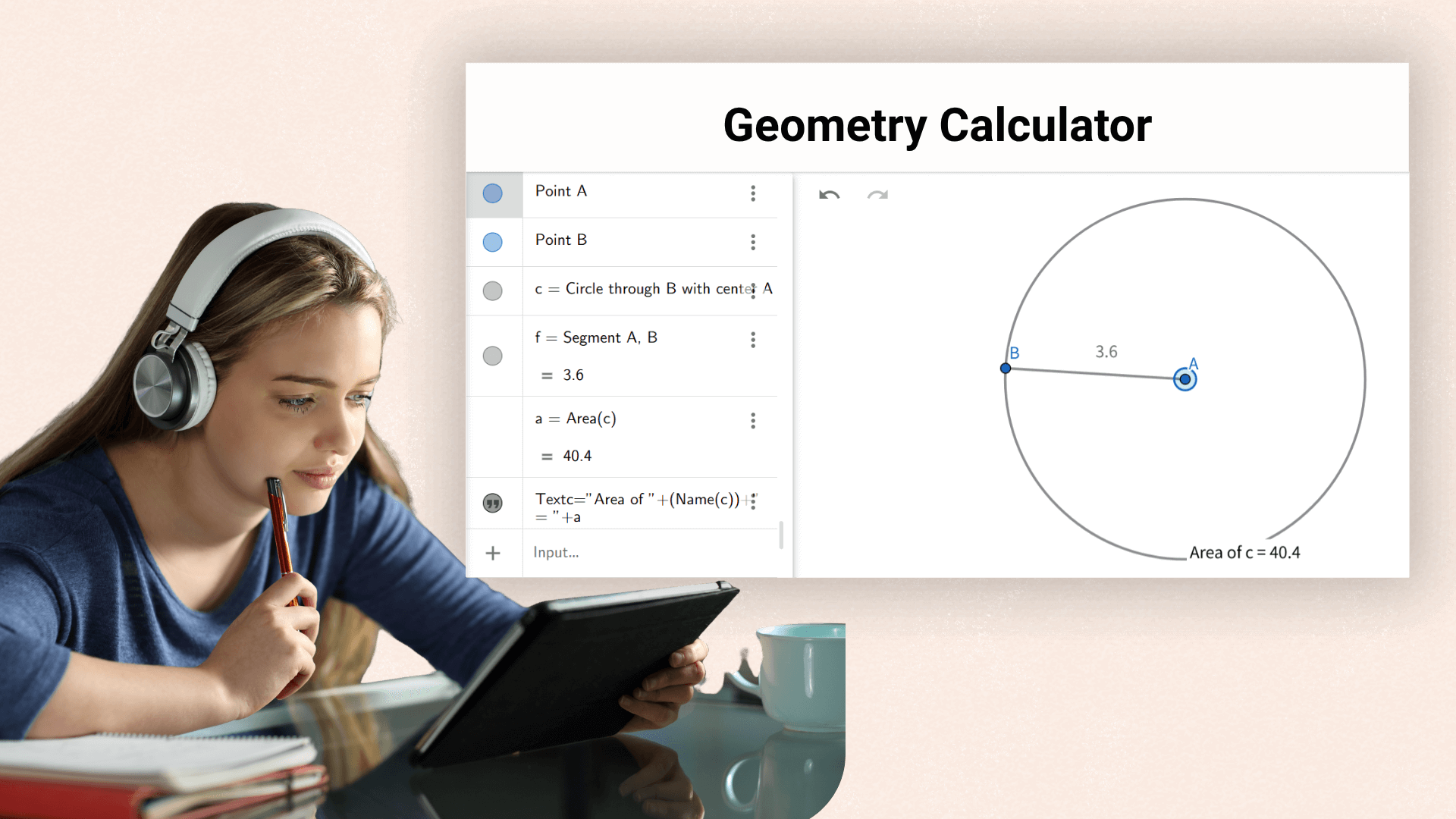
Ayuda a los estudiantes a verificar rápidamente fórmulas y resolver problemas durante los cursos de geometría, mejorando la eficiencia del aprendizaje.
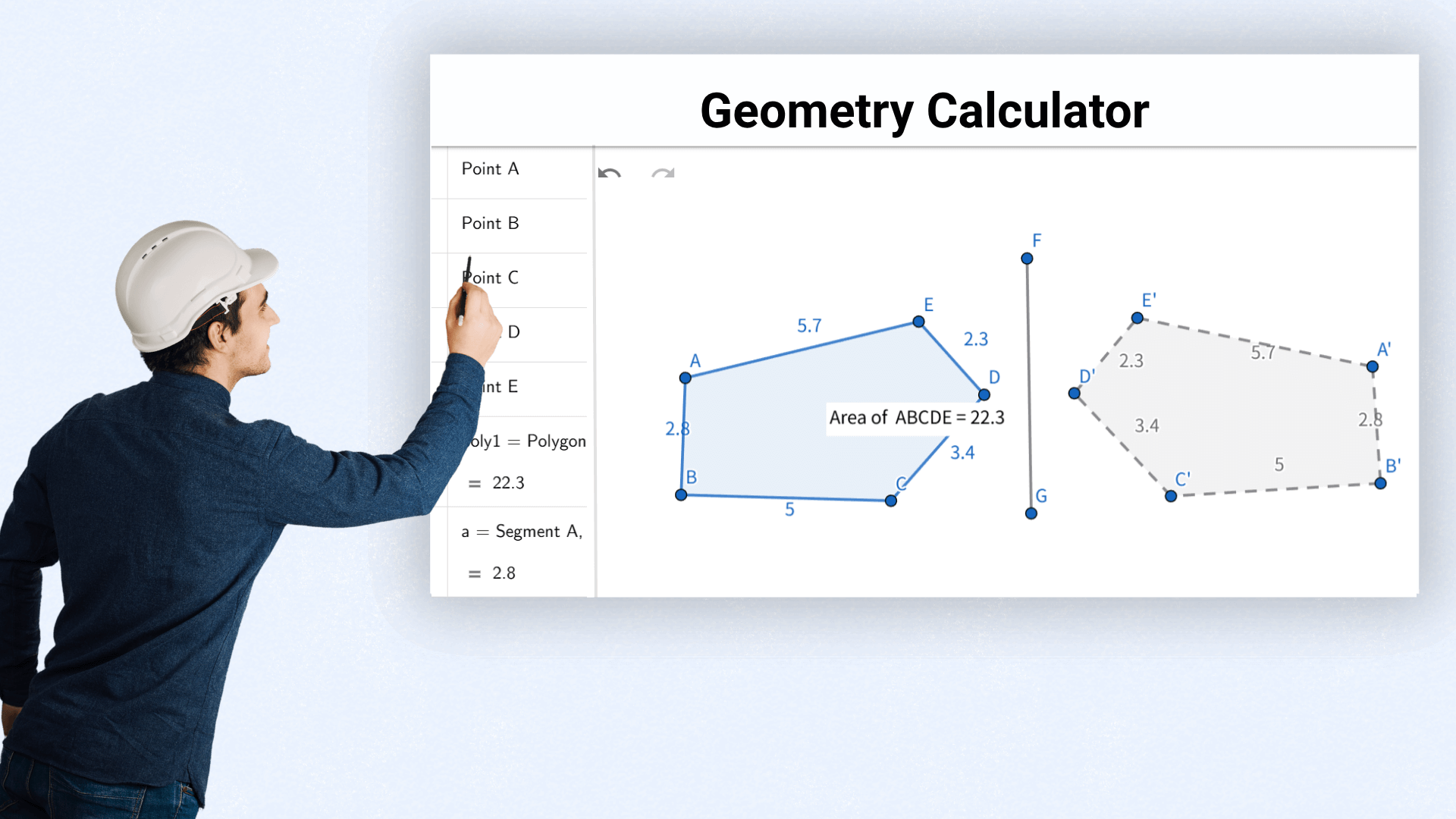
Los arquitectos calculan áreas y volúmenes para evaluar la viabilidad del diseño y optimizar la disposición espacial.

Los aficionados utilizan la calculadora de geometría para medir con precisión los materiales al crear proyectos de manualidades geométricas.
Explora la conexión entre álgebra y geometría, profundiza en la comprensión de conceptos matemáticos y utiliza la calculadora de geometría para completar tareas y proyectos.
Los profesores utilizan la calculadora para presentar visualmente conceptos geométricos durante la planificación de clases y demostraciones, mejorando la efectividad de la enseñanza.
Los ingenieros confían en la calculadora de geometría para calcular con precisión ángulos y longitudes en diseños estructurales o mecánicos, reduciendo errores por cálculos manuales.

Los aficionados utilizan la calculadora para asegurar mediciones precisas al crear manualidades basadas en geometría.
Utiliza la calculadora de geometría para esbozar y ajustar rápidamente conceptos de diseño inicial, obteniendo una comprensión clara de las relaciones espaciales antes de pasar a herramientas CAD detalladas.

Los investigadores visualizan estructuras complejas y analizan datos usando las funciones de dibujo y cálculo de la calculadora, apoyando la exploración científica.
Utiliza algoritmos avanzados para garantizar resultados geométricos de alta precisión.
Interfaz simple e intuitiva con un flujo de trabajo claro; no se necesita formación compleja, incluso para nuevos usuarios.
Integra múltiples herramientas y funciones para satisfacer diversas necesidades de cálculo geométrico en un solo lugar.
Rendimiento rápido y operación fluida, incluso con grandes cantidades de datos o fórmulas complejas.
Dibuja formas con precisión y controla su tamaño y propiedades, proporcionando una base visual confiable para el análisis y la investigación.
Todas las funciones de la calculadora de geometría en línea están disponibles sin costo, haciendo accesibles herramientas geométricas de alta calidad para todos.
Sí, es completamente gratuita. Los usuarios pueden acceder a todas las funciones sin ningún costo.
Abre nuestro sitio web, selecciona 'Nueva Geometría', luego haz clic en herramientas como 'Punto', 'Segmento' o 'Círculo' para colocar figuras en el área de dibujo.
Se utiliza ampliamente en la educación matemática y también puede ayudar en la enseñanza de geometría, álgebra y cálculo.
Dibuja o importa la figura, selecciona el objeto que deseas medir y luego elige propiedades como distancia, longitud, ángulo, perímetro o área. Los resultados aparecerán en el área de dibujo o álgebra.
Sí. La calculadora de geometría es fácil de usar y tiene una interfaz intuitiva, perfecta para que los principiantes comiencen rápidamente.
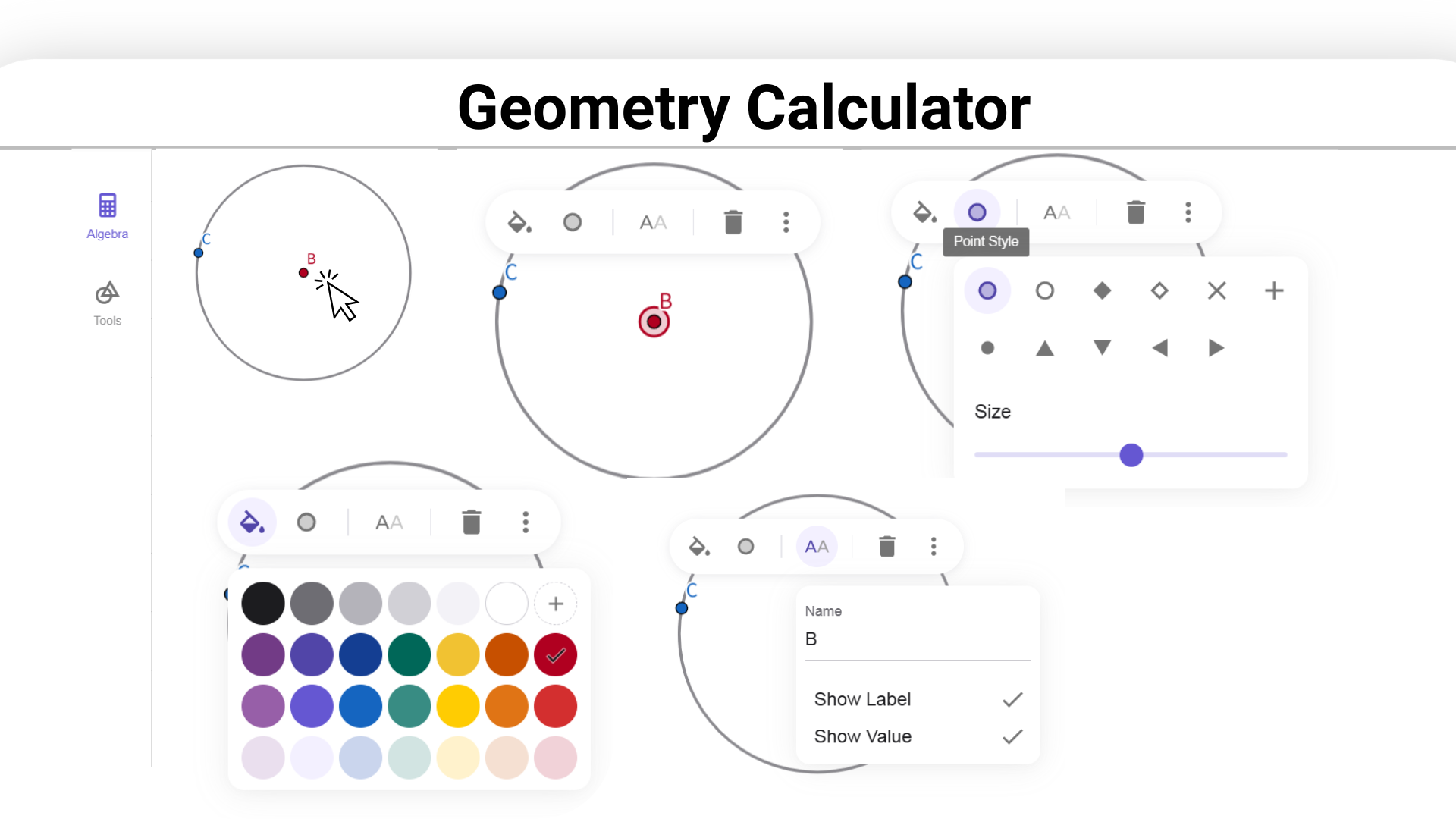
Selecciona la figura y utiliza el menú contextual o el panel de propiedades para editar su apariencia, incluyendo color, estilo de línea y relleno.
Nuestra calculadora de geometría utiliza algoritmos avanzados para ofrecer resultados precisos y fiables.
Ayuda a los estudiantes a explorar la relación entre álgebra y geometría, y les apoya para completar tareas y proyectos de investigación de manera más eficiente.