Estudiantes
La Calculadora Gráfica beneficia a los estudiantes desde el nivel elemental hasta la universidad. Ayuda a comprender conceptos matemáticos y cultiva habilidades de resolución de problemas.
Una calculadora de graficación puede resolver ecuaciones y dibujar gráficos de funciones, ayudándote a comprender intuitiva y precisamente los patrones cambiantes de las funciones.
La calculadora gráfica es una herramienta de dibujo potente y tecnológicamente avanzada que nos ayuda a trazar gráficos de funciones, realizar cálculos complejos y realizar análisis de datos. Al ajustar los parámetros para afectar la transformación de gráficos, el aprendizaje y la investigación matemáticos se vuelven más intuitivos, eficientes e interesantes.
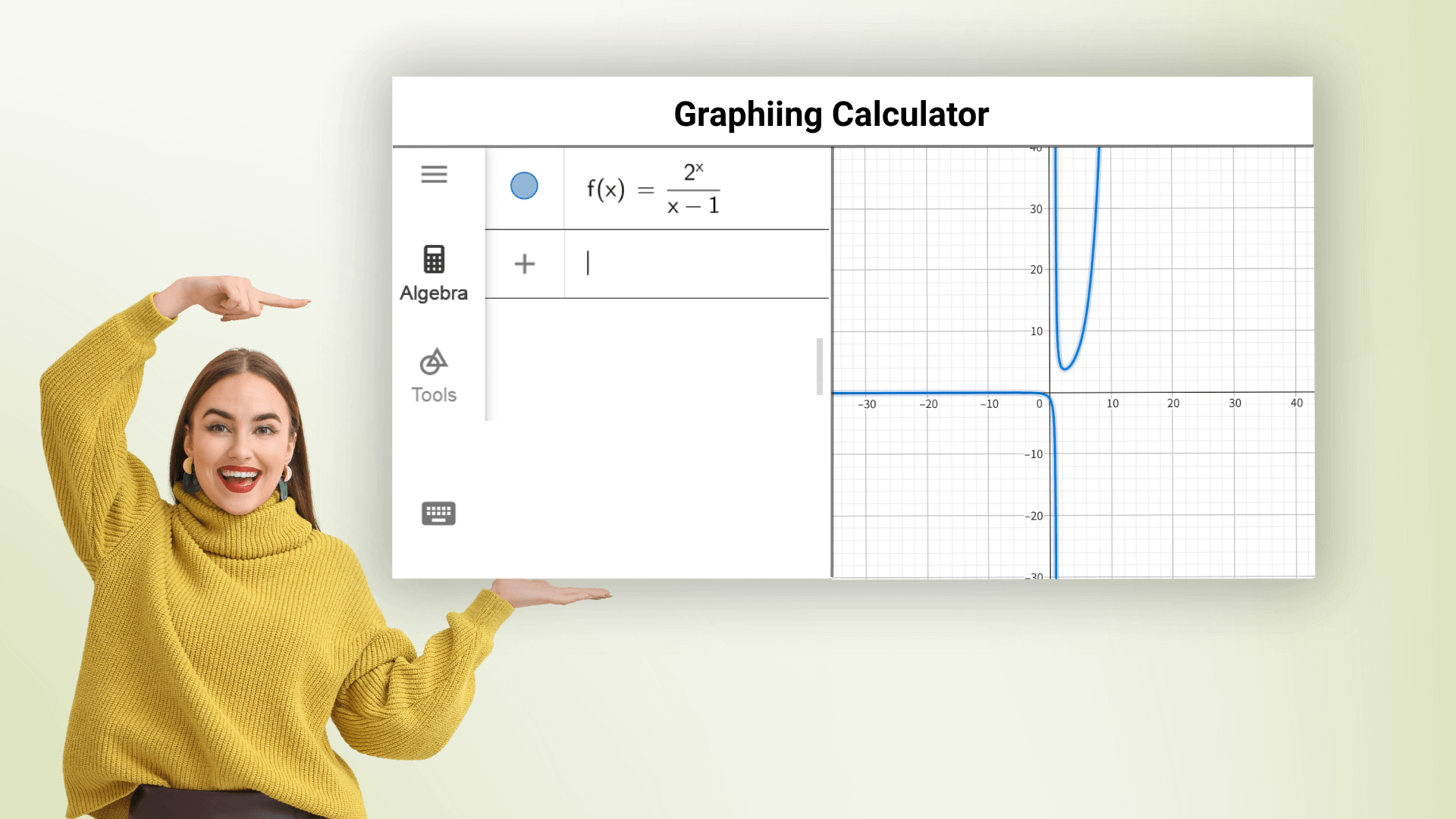
La calculadora gráfica puede trazar varios gráficos de funciones, incluidas funciones lineales, parabólicas, trigonométricas y logarítmicas, y puede graficar múltiples ecuaciones a la vez en diferentes colores. Simplemente ingrese la expresión de la función para obtener rápidamente un gráfico preciso y observe las tendencias y características de la función. La calculadora gráfica en línea ayuda a todos a dominar las matemáticas y evitar cálculos complejos.
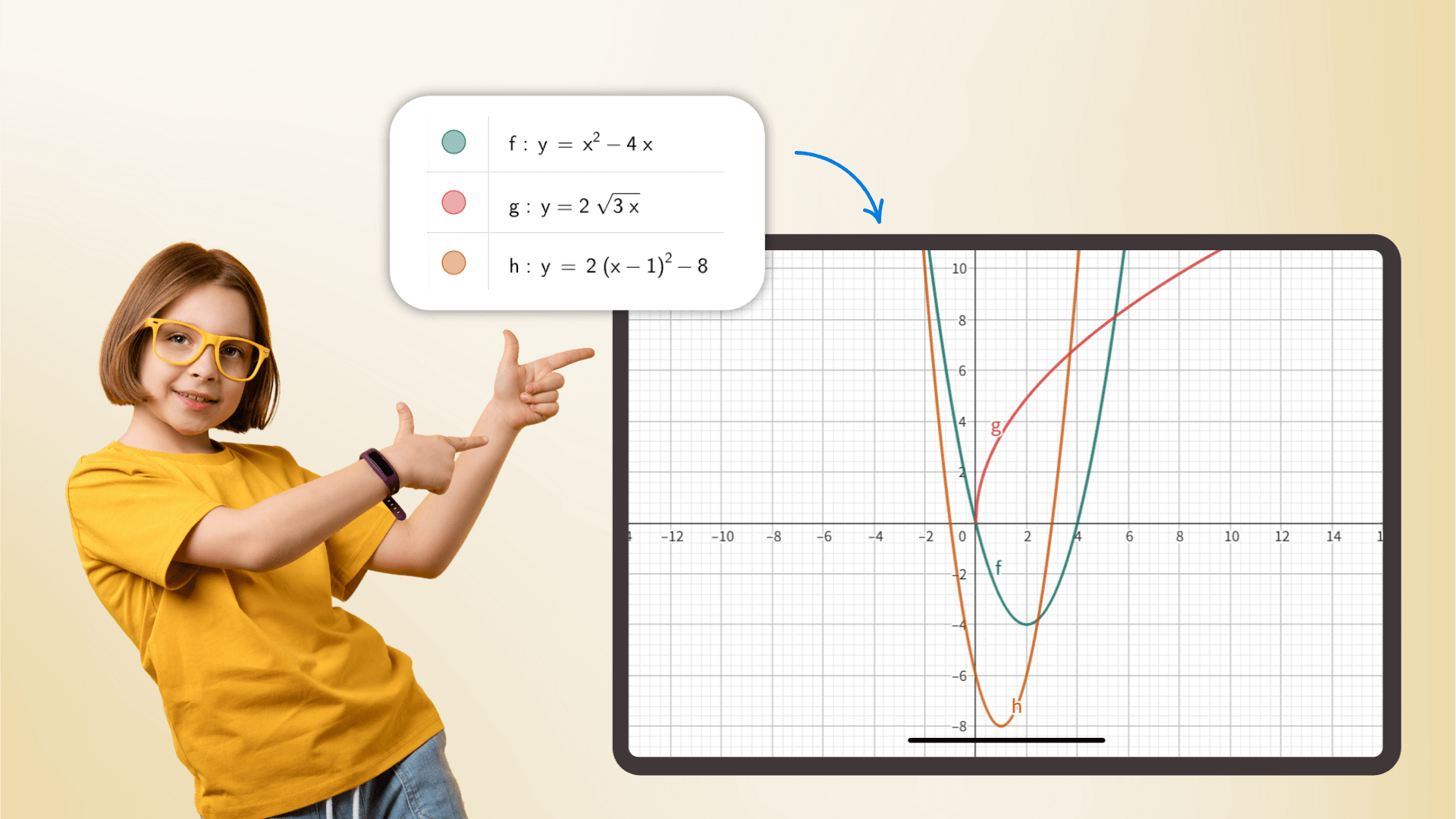
Como calculadora científica, maneja todo, desde aritmética básica hasta matemáticas avanzadas, cálculo, estadísticas de probabilidad y más. Con cálculos impulsados por la precisión, sirve como un asistente indispensable para estudiantes e investigadores por igual, elevando la eficiencia en contextos académicos y profesionales.
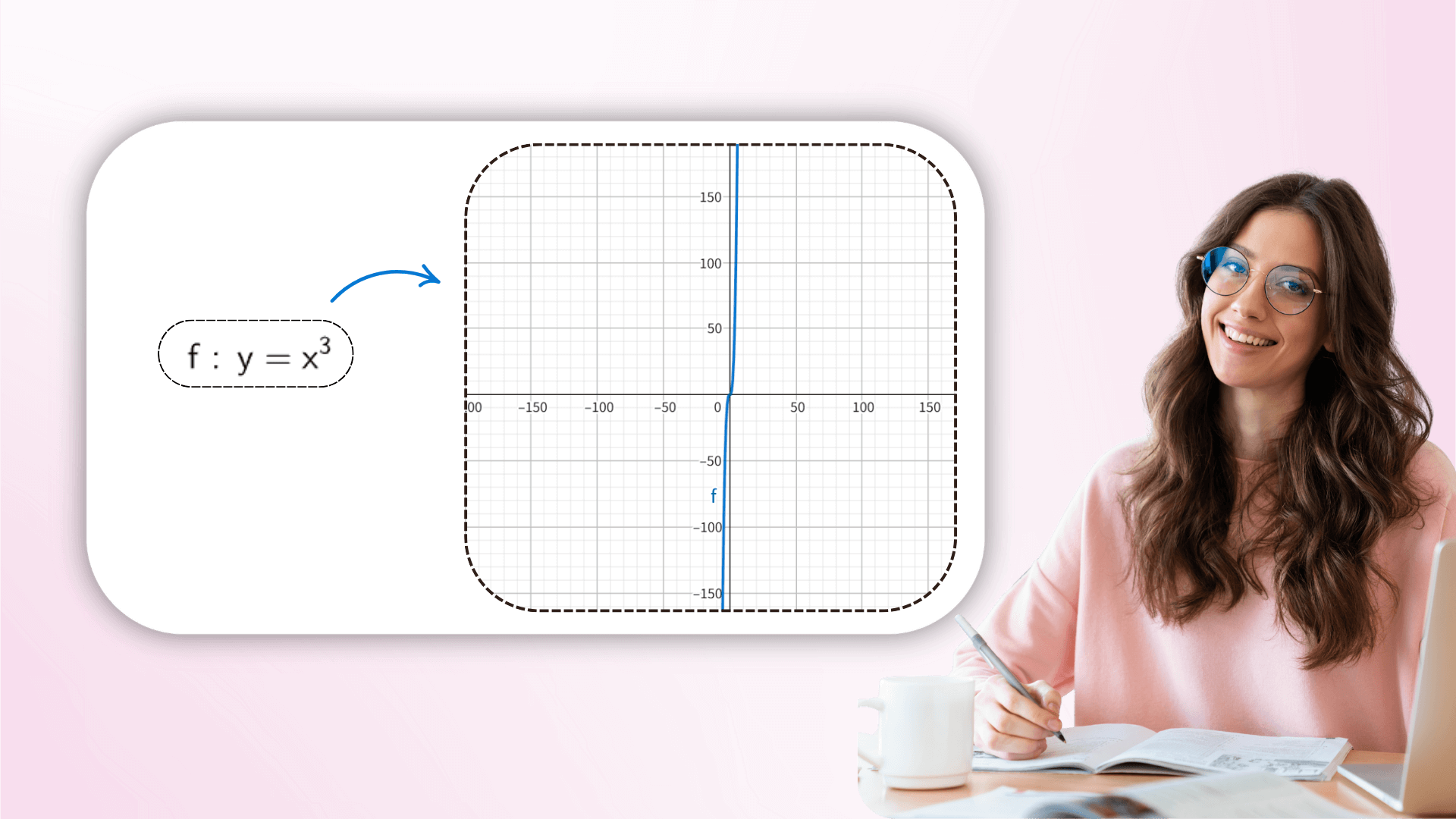
Al ajustar los valores de los parámetros en tiempo real, los usuarios pueden observar la transformación dinámica de la imagen para comprender cómo los coeficientes afectan la geometría de la función, desde la traducción lineal hasta las transformaciones complejas, vinculando fórmulas abstractas con la visión. Esta exploración interactiva puede profundizar la comprensión de las ecuaciones matemáticas.
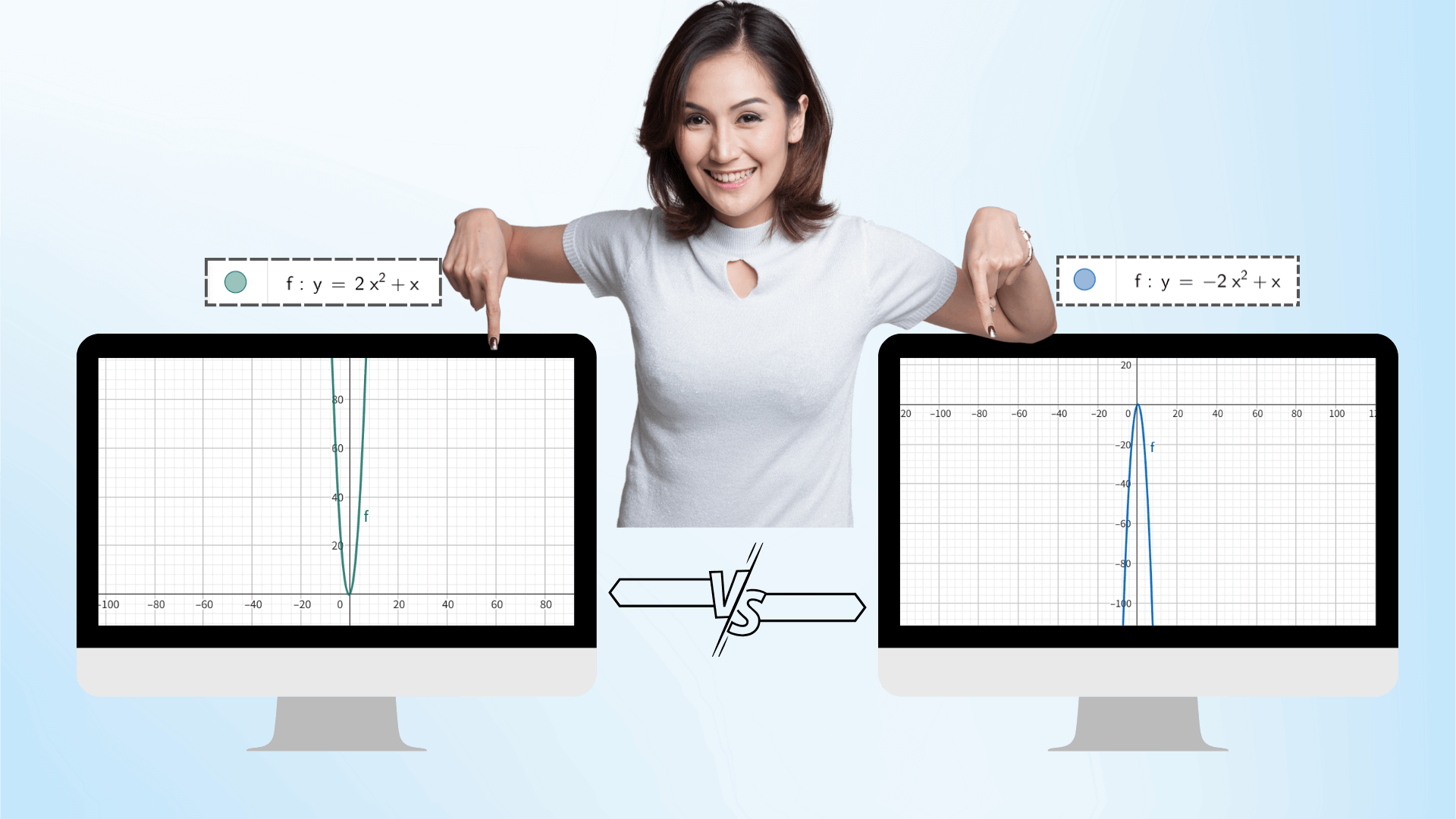
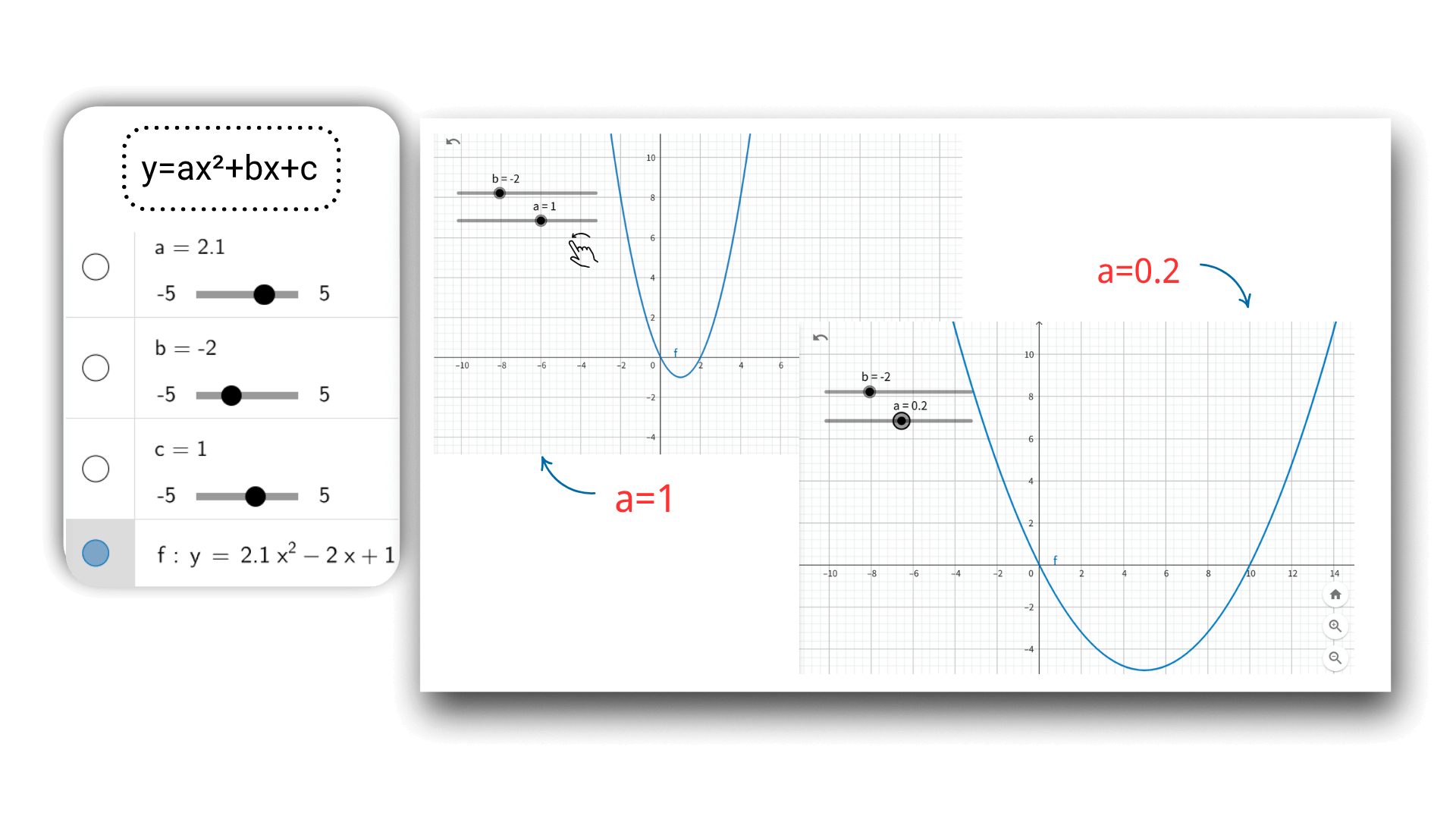
Utilizando la tecnología de graficación de AI, después de ingresar la función, puedes ajustar dinámicamente los parámetros a través del control deslizante, como a, b, c de una función cuadrática. La imagen se deformará en tiempo real como una animación, y los datos de coordenadas se actualizarán sincrónicamente, revelando intuitivamente el impacto de los cambios de parámetros en la imagen, y mejorando la comprensión de la conexión entre los conceptos matemáticos.
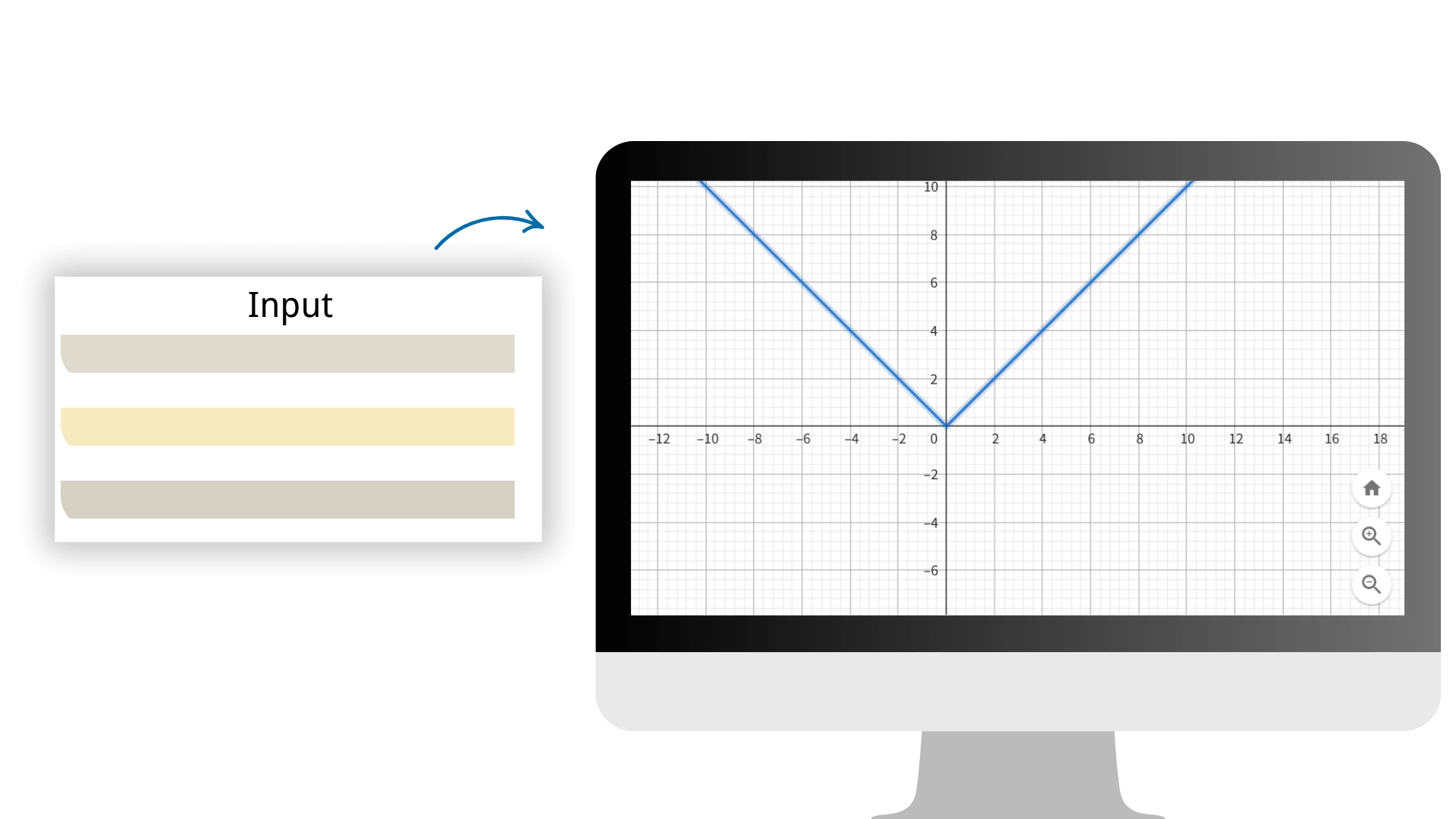
Adoptando algoritmos de cálculo avanzados, aseguramos que cada resultado de cálculo tenga una precisión extremadamente alta, proporcionando un apoyo de datos confiable para tu trabajo matemático. Simplemente ingresa el arreglo en nuestra calculadora de imágenes para generar diversas imágenes con un solo clic.
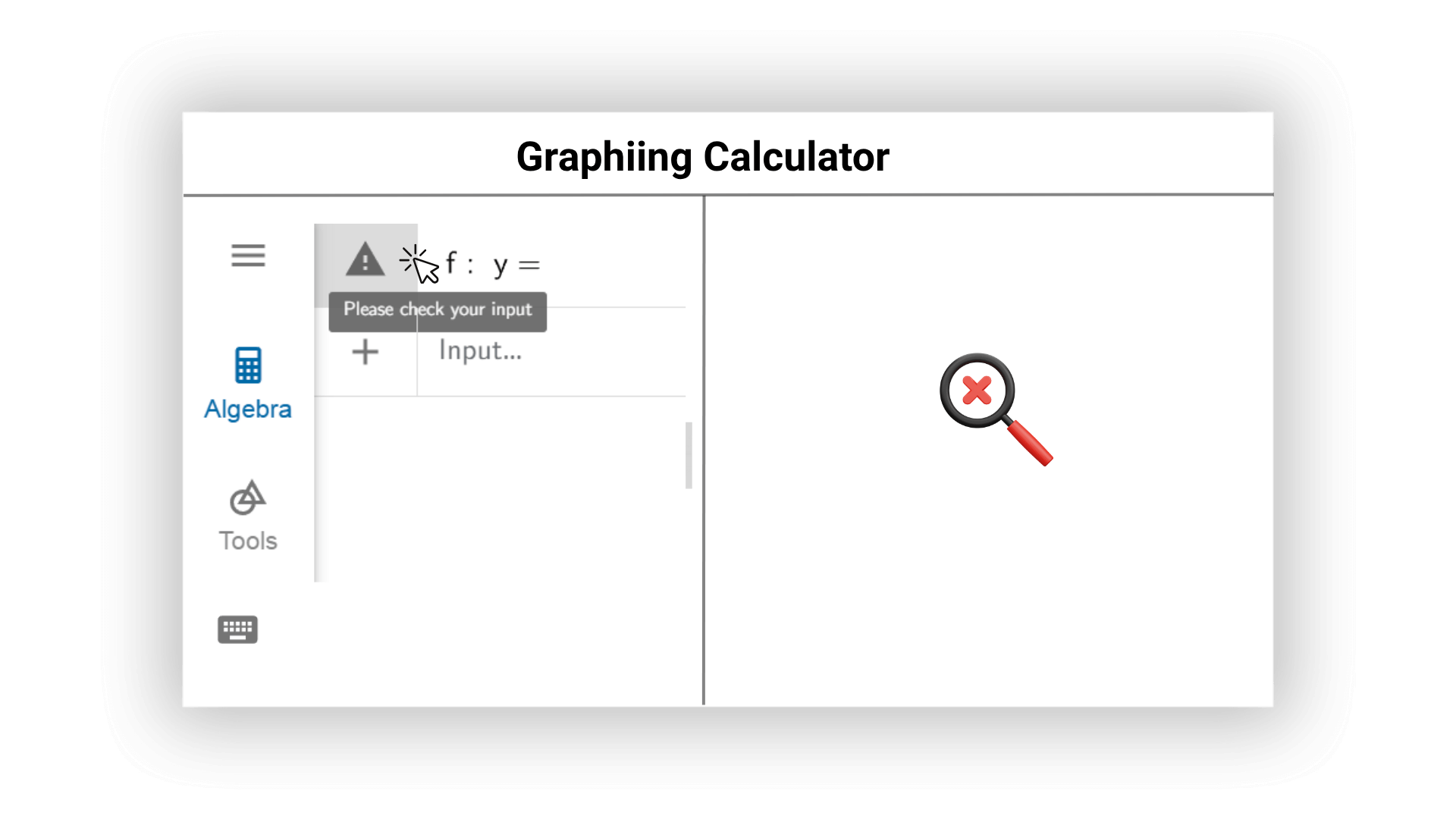
Nuestra calculadora gráfica de AI puede verificar posibles errores en expresiones matemáticas en línea en tiempo real y dar sugerencias proactivamente para la modificación. El AI puede recordar a los usuarios rápidamente los problemas gramaticales y las entradas irrazonables para asegurar resultados de cálculo precisos y una eficiencia computacional alta, y evitar errores en las imágenes y los resultados.
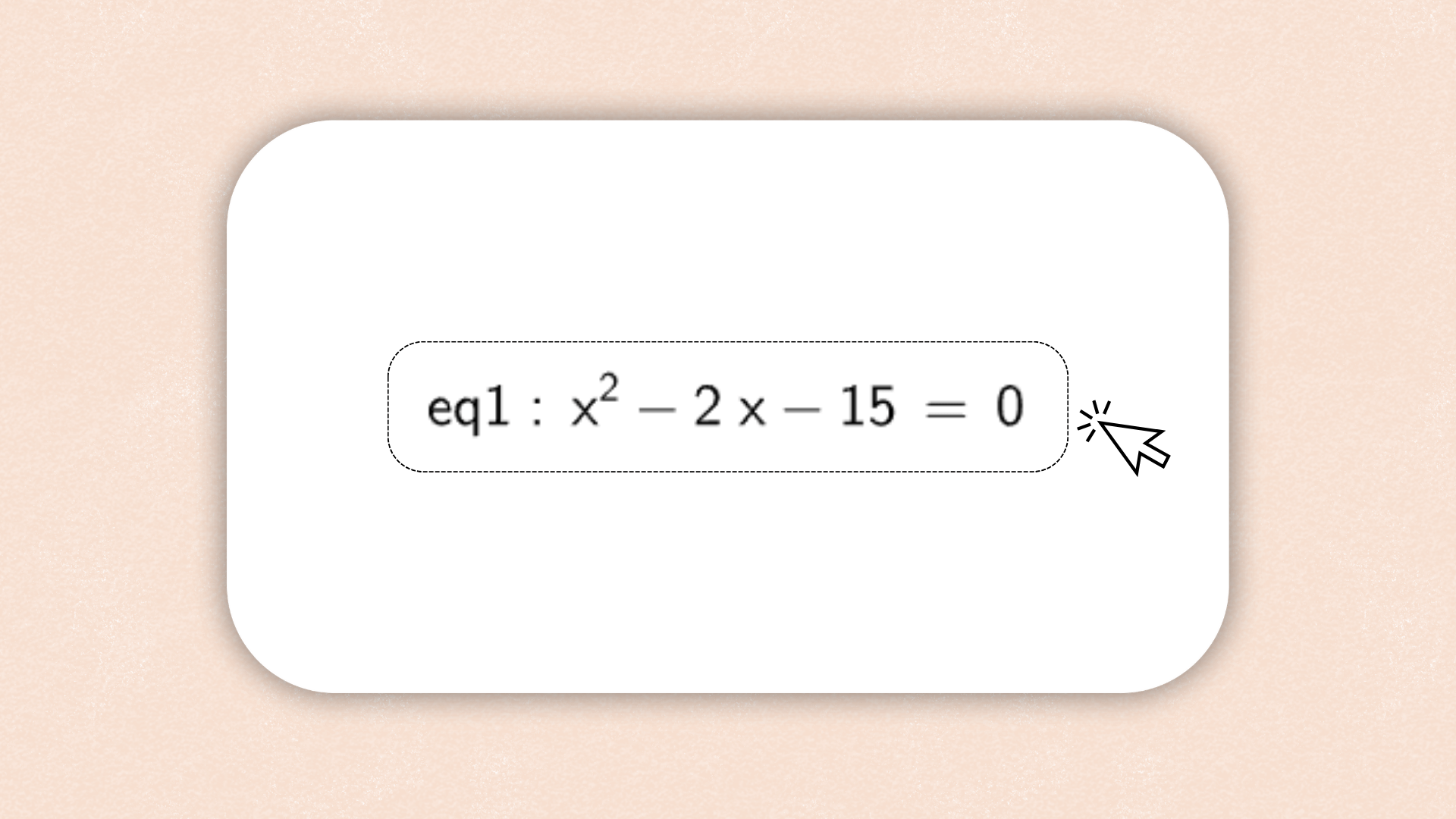
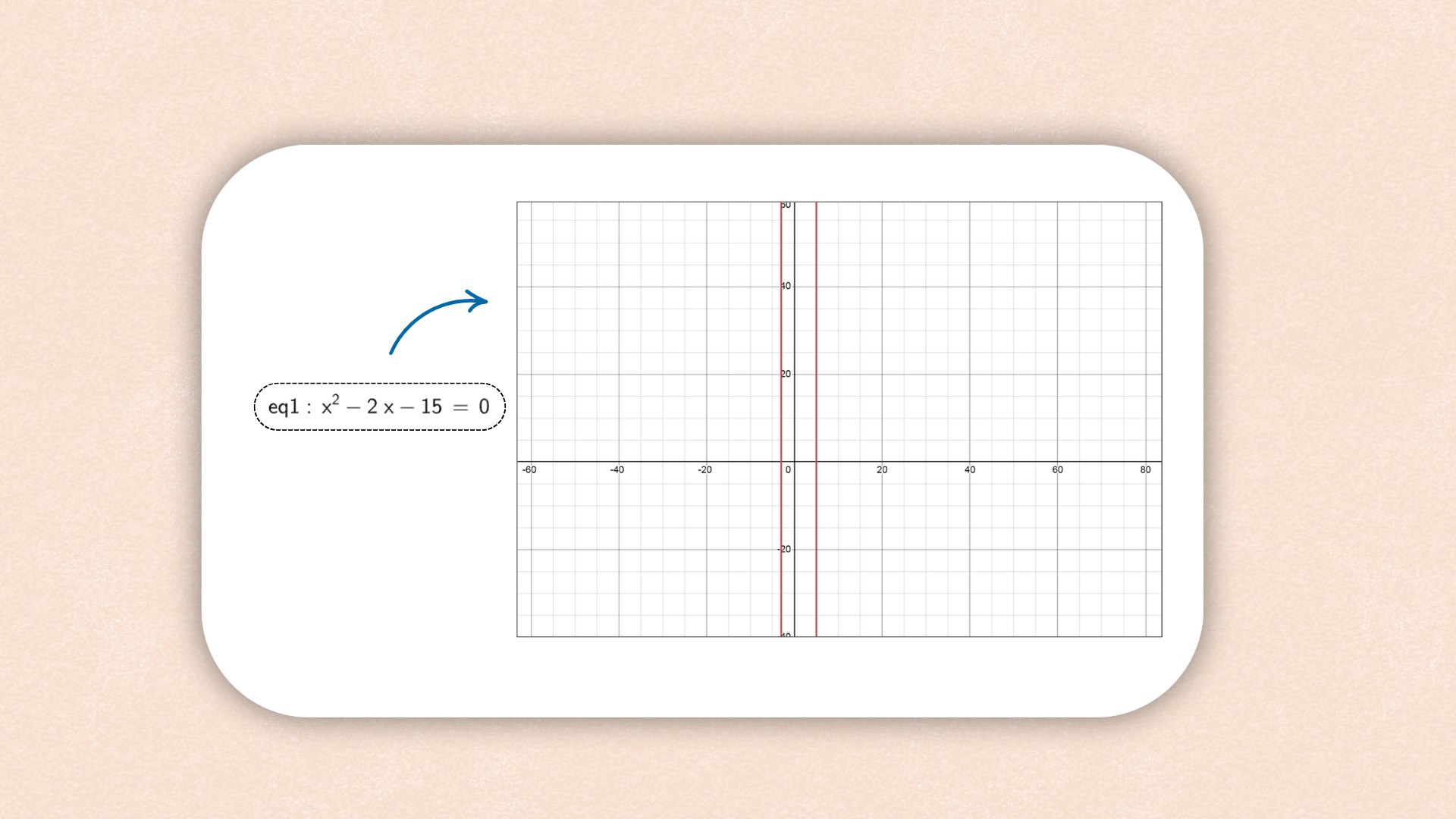
1. ![]() Introduce
Introduce y = m x + b en la Barra de Entrada
y presiona la tecla Enter.
Sugerencia: La
Calculadora Gráfica creará automáticamente deslizadores para
los parámetros m y b al presionar Enter. Para mostrar los
deslizadores en la Vista Gráfica, selecciona el botón de
Visibilidad deshabilitado en la Vista Algebraica a la
izquierda de las variables.
2. ![]() Crea el punto de intersección A entre la recta y el eje
y.
Crea el punto de intersección A entre la recta y el eje
y.
Sugerencia: Puedes usar la herramienta
Intersección que se encuentra en la Caja de Herramientas
para puntos seleccionando los dos objetos, o usar el comando
Intersect(f, yAxis).
3. ![]() Crea un punto B en el origen usando la herramienta
Intersección y seleccionando los dos ejes.
Crea un punto B en el origen usando la herramienta
Intersección y seleccionando los dos ejes.
4. ![]() Selecciona la herramienta Segmento de la Caja de
Herramientas para líneas y crea un segmento entre los puntos
A y B seleccionando ambos puntos.
Selecciona la herramienta Segmento de la Caja de
Herramientas para líneas y crea un segmento entre los puntos
A y B seleccionando ambos puntos.
Sugerencia:
Alternativamente, también puedes usar el comando Segment(A,
B).
5. ![]() Oculta los puntos A y B haciendo clic en los botones de
Visibilidad habilitados correspondientes a la izquierda de
sus coordenadas en la Vista Algebraica.
Oculta los puntos A y B haciendo clic en los botones de
Visibilidad habilitados correspondientes a la izquierda de
sus coordenadas en la Vista Algebraica.
6. ![]() Utiliza la herramienta Pendiente de la Caja de Herramientas
de Medida para crear la pendiente (triángulo) de la recta
haciendo clic sobre la recta.
Utiliza la herramienta Pendiente de la Caja de Herramientas
de Medida para crear la pendiente (triángulo) de la recta
haciendo clic sobre la recta.
7. ![]() Mejora la apariencia de tu construcción usando la Barra de
Estilo (por ejemplo, aumenta el grosor de la línea del
segmento para que sea visible sobre el eje y).
Mejora la apariencia de tu construcción usando la Barra de
Estilo (por ejemplo, aumenta el grosor de la línea del
segmento para que sea visible sobre el eje y).
1. ![]() Escribe f(x) = x^2 en la Barra de Entrada y presiona
Enter.
Escribe f(x) = x^2 en la Barra de Entrada y presiona
Enter.
¿Qué forma tiene la gráfica de la función?
2. ![]() Utiliza la herramienta Mover y selecciona la función. Haz
clic en la Barra de Estilo y selecciona desanclar la
función. Ahora puedes arrastrar la función en la Vista
Gráfica y observar cómo la ecuación en la Vista Algebraica
se adapta a tus cambios.
Utiliza la herramienta Mover y selecciona la función. Haz
clic en la Barra de Estilo y selecciona desanclar la
función. Ahora puedes arrastrar la función en la Vista
Gráfica y observar cómo la ecuación en la Vista Algebraica
se adapta a tus cambios.
3. ![]() Cambia la gráfica de la función para que la ecuación
correspondiente sea:
Cambia la gráfica de la función para que la ecuación
correspondiente sea:
f(x) = (x + 2)²
f(x) = x² - 3
y
f(x) = (x - 4)² + 2.
4. ![]() Selecciona la ecuación del polinomio. Usa el teclado para
cambiar la ecuación a f(x) = 3 x^2.
Selecciona la ecuación del polinomio. Usa el teclado para
cambiar la ecuación a f(x) = 3 x^2.
¿Cómo cambia
la gráfica de la función?
5. ![]() Repite el cambio de la ecuación escribiendo diferentes
valores para el parámetro (por ejemplo, 0.5, -2, -0.8,
3).
Repite el cambio de la ecuación escribiendo diferentes
valores para el parámetro (por ejemplo, 0.5, -2, -0.8,
3).
1. ![]() Introduce f(x) = a*x³ + b*x² + c*x + d en la Barra
de Entrada y presiona Enter.
Introduce f(x) = a*x³ + b*x² + c*x + d en la Barra
de Entrada y presiona Enter.
Sugerencia: La Calculadora Gráfica creará
automáticamente deslizadores para los parámetros a, b, c y
d.
2. ![]() Muestra los deslizadores en la Vista Gráfica seleccionando
los botones de Visibilidad deshabilitados a la izquierda de
las entradas correspondientes en la Vista Algebraica.
Muestra los deslizadores en la Vista Gráfica seleccionando
los botones de Visibilidad deshabilitados a la izquierda de
las entradas correspondientes en la Vista Algebraica.
3. ![]() Utiliza los deslizadores en la Vista Gráfica para cambiar
los valores de los parámetros con la herramienta Mover a
a = 0.2, b = -1.2, c = 0.6, d = 2.
Utiliza los deslizadores en la Vista Gráfica para cambiar
los valores de los parámetros con la herramienta Mover a
a = 0.2, b = -1.2, c = 0.6, d = 2.
4. ![]() Introduce R = Root(f) en la Barra de Entrada para
mostrar las raíces del polinomio. Las raíces se nombrarán
automáticamente R1, R2 y R3.
Introduce R = Root(f) en la Barra de Entrada para
mostrar las raíces del polinomio. Las raíces se nombrarán
automáticamente R1, R2 y R3.
5. ![]() Introduce E = Extremum(f) para mostrar los extremos
locales del polinomio.
Introduce E = Extremum(f) para mostrar los extremos
locales del polinomio.
6. ![]() Utiliza la herramienta Tangente para crear las tangentes al
polinomio a través de los extremos E1 y E2.
Utiliza la herramienta Tangente para crear las tangentes al
polinomio a través de los extremos E1 y E2.
Sugerencia: Abre la Caja de Herramientas de
Líneas Especiales y selecciona la herramienta Tangente.
Selecciona sucesivamente el punto E1 y el polinomio para
crear la tangente. Repite para el punto E2.
7. ![]() Cambia sistemáticamente los valores de los deslizadores
usando la herramienta Mover para explorar cómo los
parámetros afectan al polinomio.
Cambia sistemáticamente los valores de los deslizadores
usando la herramienta Mover para explorar cómo los
parámetros afectan al polinomio.
1. ![]() Introduce la ecuación lineal
line_1: y = m_1 x + b_1 en la Barra de Entrada.
Introduce la ecuación lineal
line_1: y = m_1 x + b_1 en la Barra de Entrada.
Sugerencia: La entrada line_1 te da la recta
1.
2. ![]() La Calculadora Gráfica creará automáticamente deslizadores
para las variables m_1 y b_1 al presionar
Enter.
La Calculadora Gráfica creará automáticamente deslizadores
para las variables m_1 y b_1 al presionar
Enter.
3. ![]() Muestra los deslizadores en la Vista Gráfica haciendo clic
en los botones de Visibilidad deshabilitados junto a su
entrada en la Vista Algebraica.
Muestra los deslizadores en la Vista Gráfica haciendo clic
en los botones de Visibilidad deshabilitados junto a su
entrada en la Vista Algebraica.
4. ![]() Repite los pasos 1 a 3 para la ecuación de
line_2: y = m_2 x + b_2.
Repite los pasos 1 a 3 para la ecuación de
line_2: y = m_2 x + b_2.
5. ![]() Utiliza la Barra de Estilo para cambiar el color de ambas
rectas y sus deslizadores.
Utiliza la Barra de Estilo para cambiar el color de ambas
rectas y sus deslizadores.
6. ![]() Utiliza la herramienta Texto y crea un texto dinámico
introduciendo Recta 1: en el cuadro de diálogo que
aparece y seleccionando line_1 de la lista de objetos
en la pestaña Objetos de la sección Avanzado.
Utiliza la herramienta Texto y crea un texto dinámico
introduciendo Recta 1: en el cuadro de diálogo que
aparece y seleccionando line_1 de la lista de objetos
en la pestaña Objetos de la sección Avanzado.
7. ![]() Crea un texto dinámico con la parte estática
Recta 2: y selecciona line_2 de la lista de
objetos en la pestaña Objetos de la sección Avanzado.
Crea un texto dinámico con la parte estática
Recta 2: y selecciona line_2 de la lista de
objetos en la pestaña Objetos de la sección Avanzado.
8. ![]() Utiliza la Barra de Estilo para igualar el color de los
textos con sus respectivas rectas.
Utiliza la Barra de Estilo para igualar el color de los
textos con sus respectivas rectas.
9. ![]() Construye el punto de intersección A de ambas
line_1 y line_2 usando la herramienta
Intersección, o introduciendo el comando
Intersect(line_1, line_2) en la Barra de
Entrada.
Construye el punto de intersección A de ambas
line_1 y line_2 usando la herramienta
Intersección, o introduciendo el comando
Intersect(line_1, line_2) en la Barra de
Entrada.
10. ![]() Introduce xcoordinate = x(A) en la Barra de
Entrada.
Introduce xcoordinate = x(A) en la Barra de
Entrada.
Sugerencia: x(A) te da la coordenada x del punto
de intersección A.
11. ![]() También define ycoordinate = y(A).
También define ycoordinate = y(A).
Sugerencia: y(A) te da la coordenada y del punto
de intersección A.
12. ![]() Crea un texto dinámico con la parte estática
Solución: x = y selecciona xcoordinate de la
lista de objetos en la pestaña Objetos.
Crea un texto dinámico con la parte estática
Solución: x = y selecciona xcoordinate de la
lista de objetos en la pestaña Objetos.
13. ![]() Crea un texto dinámico con la parte estática y = y
selecciona ycoordinate de la lista de objetos en la
pestaña Objetos.
Crea un texto dinámico con la parte estática y = y
selecciona ycoordinate de la lista de objetos en la
pestaña Objetos.
14. ![]() Fija los textos para que no puedan moverse accidentalmente
seleccionando los textos y abriendo la Barra de
Estilo.
Fija los textos para que no puedan moverse accidentalmente
seleccionando los textos y abriendo la Barra de
Estilo.
1. ![]() Introduce el polinomio f(x) = x^2/2 + 1 en la Barra
de Entrada.
Introduce el polinomio f(x) = x^2/2 + 1 en la Barra
de Entrada.
2. ![]() Crea un nuevo punto A sobre la función
f.
Crea un nuevo punto A sobre la función
f.
Sugerencia: El punto A solo puede moverse a lo
largo de la función.
3. ![]() Crea la tangente g a la función f a través
del punto A.
Crea la tangente g a la función f a través
del punto A.
4. ![]() Crea la pendiente de la tangente g usando
m = Slope(g).
Crea la pendiente de la tangente g usando
m = Slope(g).
5. ![]() Define el punto S = (x(A), m).
Define el punto S = (x(A), m).
Sugerencia: x(A) te da la coordenada x del punto
A.
6. ![]() Conecta los puntos A y S usando un
segmento.
Conecta los puntos A y S usando un
segmento.
7. ![]() Activa el rastro del punto S y mueve el punto
A.
Activa el rastro del punto S y mueve el punto
A.
Sugerencia: Haz clic derecho en el punto S
(MacOS: Ctrl-clic, tablet: pulsación larga) y selecciona
Mostrar Rastro.
1. ![]() Introduce la función f(x) = sin(x) en la Barra de
Entrada.
Introduce la función f(x) = sin(x) en la Barra de
Entrada.
2. ![]() Haz clic derecho en la Vista Gráfica y selecciona
Gráficos... . Selecciona la pestaña xAxis y cambia la unidad
a
Haz clic derecho en la Vista Gráfica y selecciona
Gráficos... . Selecciona la pestaña xAxis y cambia la unidad
a π.
3. ![]() Crea un nuevo punto A sobre la función
f.
Crea un nuevo punto A sobre la función
f.
Sugerencia: El punto A solo puede moverse a lo
largo de la función.
4. ![]() Crea la tangente g a la función f a través
del punto A.
Crea la tangente g a la función f a través
del punto A.
5. ![]() Crea la pendiente de la tangente g usando la
herramienta Pendiente.
Crea la pendiente de la tangente g usando la
herramienta Pendiente.
6. ![]() Define el punto S = (x(A), m).
Define el punto S = (x(A), m).
Sugerencia: x(A) te da la coordenada x del punto
A.
7. ![]() Conecta los puntos A y S usando un
segmento.
Conecta los puntos A y S usando un
segmento.
8. ![]() Activa el rastro del punto S y mueve el punto
A.
Activa el rastro del punto S y mueve el punto
A.
Sugerencia: Haz clic derecho en el punto S
(MacOS: Ctrl-clic, tablet: pulsación larga) y selecciona
Mostrar Rastro.
9. ![]() Haz clic derecho (MacOS: Ctrl-clic, tablet: pulsación
larga) en el punto A y elige Animación en el
menú contextual.
Haz clic derecho (MacOS: Ctrl-clic, tablet: pulsación
larga) en el punto A y elige Animación en el
menú contextual.
Sugerencia: Aparecerá un botón de Animación en
la esquina inferior izquierda de la Vista Gráfica. Te
permite pausar o continuar la animación.
1. ![]() Introduce a x + b y ≤ c en la Barra de Entrada y
presiona Enter.
Introduce a x + b y ≤ c en la Barra de Entrada y
presiona Enter.
Sugerencia: Puedes usar el
Teclado Virtual para ingresar el símbolo ≤. La Calculadora
Gráfica creará automáticamente deslizadores para los
parámetros a, b y c.
2. ![]() Utiliza la herramienta Mover para ajustar los valores de
los deslizadores de modo que a = 1, b = 1 y c = 3.
Utiliza la herramienta Mover para ajustar los valores de
los deslizadores de modo que a = 1, b = 1 y c = 3.
3. ![]() Cambia el incremento de los deslizadores a 1.
Cambia el incremento de los deslizadores a 1.
Sugerencia:
Selecciona el número a y abre la Barra de Estilo de la Vista
Gráfica.
Abre la configuración del número a y selecciona la pestaña
Deslizador.
Establece el incremento en 1 y repite para los números b y
c.
4. ![]() Arrastra el fondo de la Vista Gráfica para mover el origen
al centro.
Arrastra el fondo de la Vista Gráfica para mover el origen
al centro.
5. ![]() Aleja para hacer visible una mayor parte del sistema de
coordenadas en la pantalla.
Aleja para hacer visible una mayor parte del sistema de
coordenadas en la pantalla.
6. ![]() Establece la distancia entre las marcas de los ejes en
1.
Establece la distancia entre las marcas de los ejes en
1.
Sugerencia:
Asegúrate de que ningún objeto esté seleccionado antes de
abrir la Barra de Estilo de la Vista Gráfica.
Abre la configuración de los ejes.
Selecciona la pestaña xAxis y establece la distancia en 1.
Repite en la pestaña yAxis.
1. ![]() Introduce
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) en
la Barra de Entrada y presiona Enter.
Introduce
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) en
la Barra de Entrada y presiona Enter.
2. ![]() Crea un deslizador s para un número con intervalo de
1 a 10 e incremento 1.
Crea un deslizador s para un número con intervalo de
1 a 10 e incremento 1.
3. ![]() Introduce Sequence((i, i), i, 0, s) en la Barra de
Entrada y presiona Enter.
Introduce Sequence((i, i), i, 0, s) en la Barra de
Entrada y presiona Enter.
4. ![]() Mueve el deslizador s para comprobar la
construcción.
Mueve el deslizador s para comprobar la
construcción.
1. ![]() Abre la Configuración de la Vista Gráfica usando la Barra
de Estilo.
Abre la Configuración de la Vista Gráfica usando la Barra
de Estilo.
2. ![]() En la pestaña xAxis, establece la distancia de las marcas
en 1 marcando la casilla Distancia e ingresando 1 en el
campo de texto.
En la pestaña xAxis, establece la distancia de las marcas
en 1 marcando la casilla Distancia e ingresando 1 en el
campo de texto.
3. ![]() En la pestaña Básico, establece el mínimo del eje x en -11
y el máximo en 11.
En la pestaña Básico, establece el mínimo del eje x en -11
y el máximo en 11.
4. ![]() En la pestaña yAxis, desmarca Mostrar eje y y cierra la
Configuración.
En la pestaña yAxis, desmarca Mostrar eje y y cierra la
Configuración.
5. ![]() Crea dos deslizadores a y b, ambos con
intervalo de -5 a 5 e incremento 1.
Crea dos deslizadores a y b, ambos con
intervalo de -5 a 5 e incremento 1.
6. ![]() Muestra el valor de los deslizadores en lugar de sus
nombres usando la Barra de Estilo.
Muestra el valor de los deslizadores en lugar de sus
nombres usando la Barra de Estilo.
7. ![]() Crea los puntos A = (0, 1) y
B = A + (a, 0).
Crea los puntos A = (0, 1) y
B = A + (a, 0).
Sugerencia: La distancia del punto B al punto A
está determinada por el deslizador a.
8. ![]() Crea un vector u = Vector(A, B) que tiene la
longitud a.
Crea un vector u = Vector(A, B) que tiene la
longitud a.
9. ![]() Crea los puntos C = B + (0, 1) y
D = C + (b, 0).
Crea los puntos C = B + (0, 1) y
D = C + (b, 0).
10. ![]() Crea el vector v = Vector(C, D) que tiene la
longitud b.
Crea el vector v = Vector(C, D) que tiene la
longitud b.
11. ![]() Crea el punto R = (x(D), 0).
Crea el punto R = (x(D), 0).
Sugerencia: La entrada x(D) te da la coordenada
x del punto D. Así, el punto R muestra el resultado de la
suma en la recta numérica.
12. ![]() Crea el punto Z = (0, 0).
Crea el punto Z = (0, 0).
13. ![]() Crea tres segmentos c = Segment(Z, A),
d = Segment(B, C) y e = Segment(D, R).
Crea tres segmentos c = Segment(Z, A),
d = Segment(B, C) y e = Segment(D, R).
14. ![]() Utiliza la Barra de Estilo para mejorar tu construcción
(por ejemplo, igualar el color de deslizadores y vectores,
cambiar el estilo de línea, fijar deslizadores, ocultar
etiquetas y puntos).
Utiliza la Barra de Estilo para mejorar tu construcción
(por ejemplo, igualar el color de deslizadores y vectores,
cambiar el estilo de línea, fijar deslizadores, ocultar
etiquetas y puntos).
1. ![]() Crea un deslizador horizontal llamado Columnas para
un número con intervalo de 1 a 10, incremento 1 y ancho
300.
Crea un deslizador horizontal llamado Columnas para
un número con intervalo de 1 a 10, incremento 1 y ancho
300.
Sugerencia: Puedes cambiar el ancho del
deslizador en la pestaña Configuración bajo
Deslizador.
2. ![]() Crea un nuevo punto A.
Crea un nuevo punto A.
3. ![]() Construye el segmento f con la longitud dada
Columnas comenzando desde el punto A.
Construye el segmento f con la longitud dada
Columnas comenzando desde el punto A.
4. ![]() Mueve el deslizador Columnas para observar el segmento con
la longitud especificada.
Mueve el deslizador Columnas para observar el segmento con
la longitud especificada.
5. ![]() Construye una recta perpendicular g al segmento f a
través del punto A.
Construye una recta perpendicular g al segmento f a
través del punto A.
6. ![]() Construye una recta perpendicular h al segmento f a
través del punto B.
Construye una recta perpendicular h al segmento f a
través del punto B.
7. ![]() Crea un deslizador vertical llamado Filas para un
número con intervalo de 1 a 10, incremento 1 y ancho 300.
Crea un deslizador vertical llamado Filas para un
número con intervalo de 1 a 10, incremento 1 y ancho 300.
Sugerencia:
Puedes seleccionar la orientación del deslizador en el
diálogo Deslizador bajo la pestaña Deslizador.
8. ![]() Crea un círculo c con centro en A y radio
Filas.
Crea un círculo c con centro en A y radio
Filas.
9. ![]() Mueve el deslizador Filas para observar el círculo con el
radio especificado.
Mueve el deslizador Filas para observar el círculo con el
radio especificado.
10. ![]() Interseca el círculo c con la recta g para obtener el punto
de intersección C.
Interseca el círculo c con la recta g para obtener el punto
de intersección C.
Sugerencia: Al
seleccionar la herramienta Intersección haz clic en el punto
de intersección sobre el punto A para crear solo ese
punto.
11. ![]() Crea una recta paralela i al segmento f a través del
punto de intersección C.
Crea una recta paralela i al segmento f a través del
punto de intersección C.
12. ![]() Interseca las rectas i y h para obtener el punto de
intersección D.
Interseca las rectas i y h para obtener el punto de
intersección D.
13. ![]() Construye un polígono ABDC.
Construye un polígono ABDC.
14. ![]() Oculta todas las rectas, el círculo c y el segmento
f.
Oculta todas las rectas, el círculo c y el segmento
f.
15. ![]() Oculta las etiquetas de los segmentos usando la Barra de
Estilo.
Oculta las etiquetas de los segmentos usando la Barra de
Estilo.
16. ![]() Establece ambos deslizadores Columnas y Filas en el valor
10.
Establece ambos deslizadores Columnas y Filas en el valor
10.
17. ![]() Crea una lista de segmentos verticales usando:
Crea una lista de segmentos verticales usando: Sequence(Segment(A + i*(1, 0), C + i*(1, 0)), i, 1,
Columnas)
Nota: A + i*(1, 0) especifica una serie de puntos comenzando
en el punto A con distancia 1 entre sí.
C + i*(1, 0)
especifica una serie de puntos comenzando en el punto C con
distancia 1 entre sí.
Segment(A + i*(1, 0), C + i*(1,
0)) crea una lista de segmentos entre pares de estos puntos.
Nota que los extremos de los segmentos no se muestran en la
Vista Gráfica.
El deslizador Columnas determina el
número de segmentos creados.
18. ![]() Crea una lista de segmentos horizontales.
Crea una lista de segmentos horizontales.Sequence(Segment(A + i*(0, 1), B + i*(0, 1)), i, 1,
Filas)
19. ![]() Mueve los deslizadores Columnas y Filas para observar la
construcción.
Mueve los deslizadores Columnas y Filas para observar la
construcción.
20. ![]() Inserta texto estático y dinámico para expresar el problema
de multiplicación usando los valores de Columnas y Filas
como factores:
Inserta texto estático y dinámico para expresar el problema
de multiplicación usando los valores de Columnas y Filas
como factores:texto1: Columnastexto2: *texto3: Filastexto4: =
21. ![]() Calcula el resultado de la multiplicación:
Calcula el resultado de la multiplicación:
resultado = Columnas * Filas
22. ![]() Inserta texto dinámico5:
Inserta texto dinámico5: resultado
23. ![]() Oculta los puntos A, B, C y D.
Oculta los puntos A, B, C y D.
24. ![]() Mejora tu construcción usando la Barra de Estilo.
Mejora tu construcción usando la Barra de Estilo.
La calculadora gráfica de AI es un asistente poderoso para los estudiantes para aprender matemáticas. Desde la escuela secundaria hasta la universidad, es algebra, geometría, cálculo o estadísticas que pueden ayudar a los estudiantes a comprender y dominar mejor el conocimiento matemático y mejorar la eficiencia y los grados de aprendizaje. Los maestros pueden usarla para realizar demostraciones de enseñanza y crear material didáctico vívido para estimular el interés y el entusiasmo de los estudiantes en el aprendizaje.
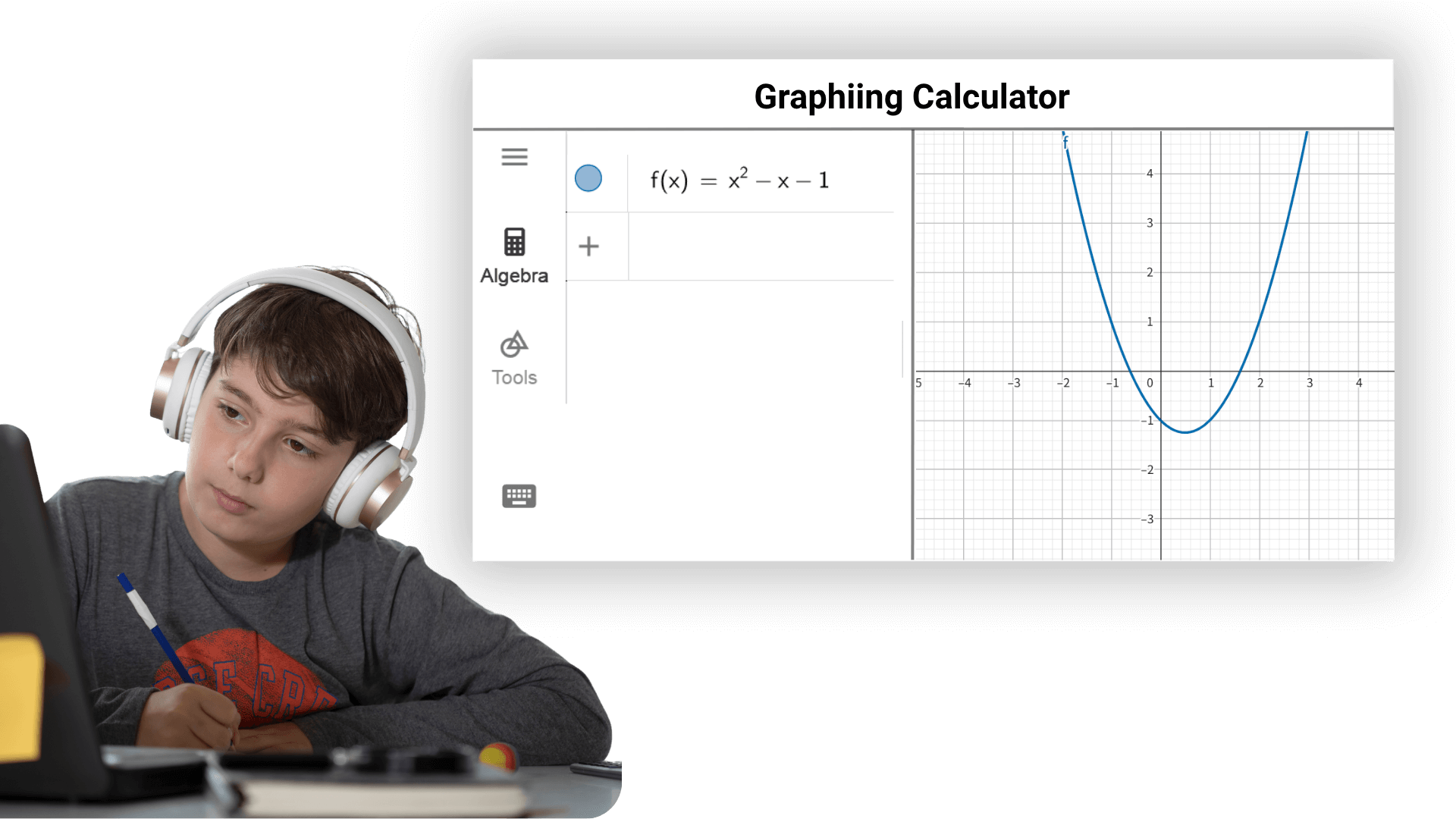
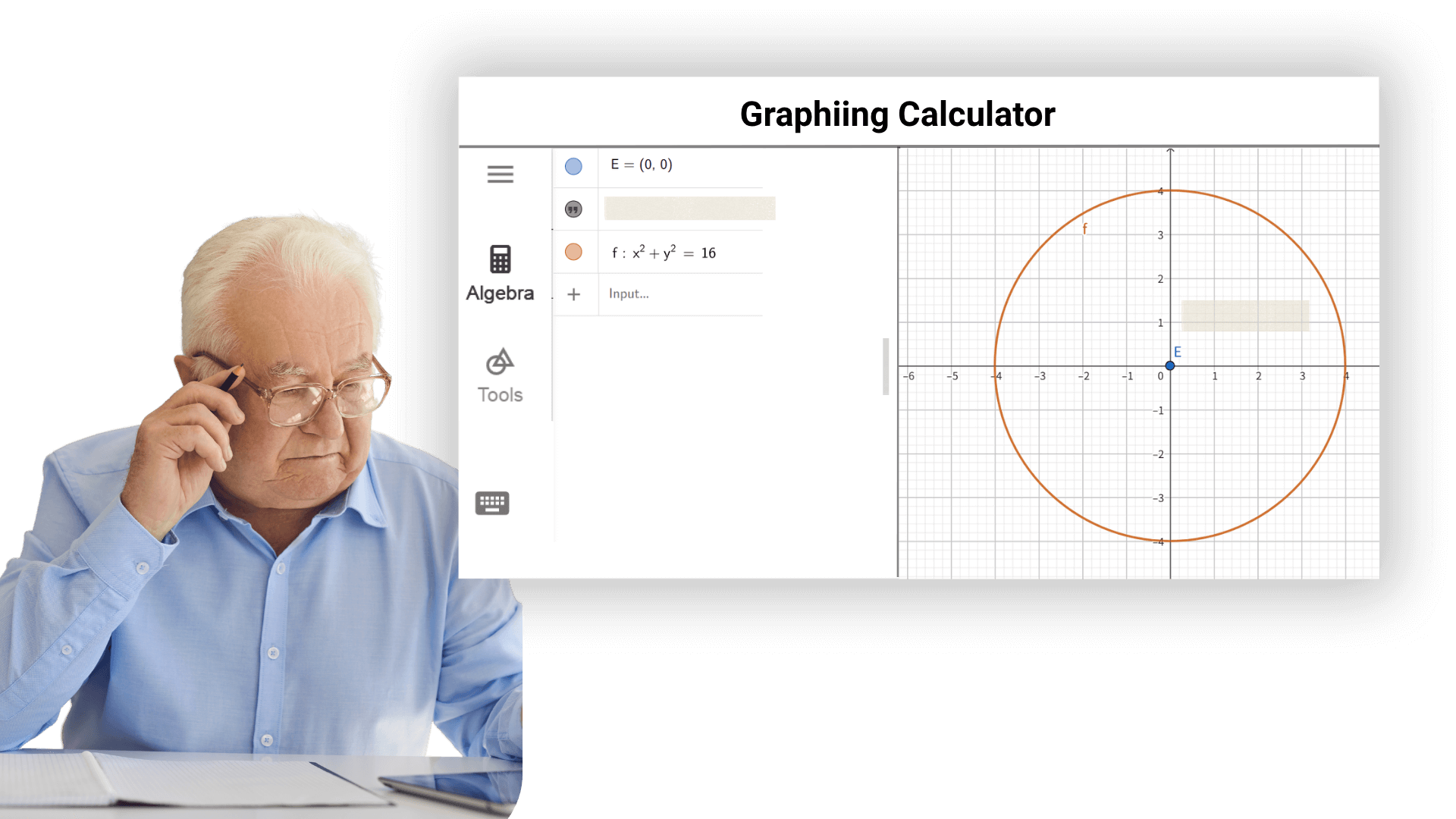
Proporciona a los investigadores herramientas matemáticas poderosas para facilitar el procesamiento de datos, el análisis experimental, la construcción de modelos y la verificación teórica. En varios campos científicos como la física, la química, la biología y la ingeniería, las calculadoras gráficas pueden ser utilizadas para completar rápidamente y con precisión operaciones matemáticas complejas y análisis de datos, asistiendo el desarrollo suave de la investigación científica.
Usa la calculadora gráfica para dibujar curvas de oferta y demanda, modelos de crecimiento compuesto, etc., analizar el punto de intersección de las funciones de costos marginales y de ingresos, y asistir en la toma de decisiones empresariales.
La Calculadora Gráfica beneficia a los estudiantes desde el nivel elemental hasta la universidad. Ayuda a comprender conceptos matemáticos y cultiva habilidades de resolución de problemas.

Los maestros de matemáticas pueden usar la calculadora gráfica para crear materiales de lección y demostrar conceptos y procesos de resolución de problemas, lo que mejora la efectividad y la interacción en la enseñanza.

Los investigadores en varios campos confían en ella para cálculos matemáticos complejos y análisis de datos. La calculadora gráfica en línea proporciona resultados precisos y acelera la investigación.

Despidete del dibujo manual tedioso, genera gráficos de visualización de datos profesionales con un solo clic, dibuja gráficos de funciones en línea, anota la media y la varianza en tiempo real, ajusta dinámicamente curvas de regresión, y completa eficientemente la integración y el análisis de datos.

Las calculadoras gráficas ayudan a los ingenieros de software a visualizar algoritmos de filtrado y a optimizar parámetros de renderizado, asegurando un rendimiento de función pixel-perfect.

Para los diseñadores arquitectónicos, las calculadoras gráficas son potentes herramientas de diseño paramétrico, ingresan ecuaciones de curvas para generar gráficos de función/desplazamiento, validan visualmente la mecánica estructural, y reducen los ciclos de diseño.

Todas las funciones no requieren registro ni pago, y puedes usarlas en todo momento.
Mantener alta precisión al calcular problemas avanzados como determinantes de matrices e integrales para evitar errores en la investigación científica.
El cálculo se completa completamente en el navegador, no se carga ningún dato y la página se borra cuando se cierra.
No es necesario descargar ni instalar, los teléfonos móviles y los ordenadores pueden usarse inmediatamente.
Enfóquese en la esencia del aprendizaje, sin ventanas emergentes, sin anuncios y mejore la concentración.
Ya sea para aplicaciones académicas, investigación científica, oficina o ingeniería, podemos satisfacer tus necesidades de cálculo gráfico.
No necesitas registrarte ni descargar ningún software. Simplemente ingresa nuestro sitio web en tu navegador y comienza a usar esta poderosa herramienta de calculadora gráfica. Puedes experimentar su conveniencia instantáneamente.
Sí, nuestra calculadora gráfica de IA es completamente gratuita. A pesar de ser gratuita, no restringe ninguna de las características principales. Puedes utilizar plenamente sus funciones de graficación, cálculo y análisis de datos sin costo alguno. Nuestro objetivo es proporcionar una herramienta matemática conveniente y eficiente para todos.
Priorizamos la seguridad y la privacidad de tus datos. Todas tus calculaciones, gráficos y datos de entrada se procesan localmente en tu navegador y nunca se cargan ni se almacenan en nuestros servidores. Puedes usarla con confianza, sabiendo que tus datos están seguros.
Para ingresar una función, simplemente escribe la fórmula en el cuadro de entrada en la página de inicio. Por ejemplo, escribe "y=2x^2" o "f(x)=sen(x)". La calculadora automáticamente procesará tu entrada y mostrará el gráfico.
Sí, la Calculadora Gráfica de IA puede manejar una variedad de funciones, desde ecuaciones lineales simples hasta avanzadas como integrales, derivadas y ecuaciones multivariables. Es adecuada para necesidades matemáticas básicas y avanzadas, lo que la hace ideal para estudiantes y profesionales.
Sí, es completamente accesible en dispositivos móviles. Puedes usarla en smartphones o tabletas, y está optimizada para todos los tamaños de pantalla, asegurando una experiencia sin problemas dondequiera que estés.