Étudiants
Explorez le lien entre l'algèbre et la géométrie, approfondissez la compréhension des concepts mathématiques et utilisez le calculateur pour réaliser devoirs et projets.
Le calculateur de géométrie peut dessiner des figures géométriques et calculer leurs propriétés, ce qui fournit une solution efficace pour l'apprentissage et l'exploration de problèmes de géométrie.
Le calculateur de géométrie est un outil puissant qui intègre des fonctions d'algèbre, de géométrie et d'analyse de données. Il est conçu pour l'apprentissage, l'enseignement et la recherche géométrique. Le calculateur de géométrie en ligne aide les utilisateurs à explorer et à résoudre des problèmes géométriques de manière plus intuitive et efficace.
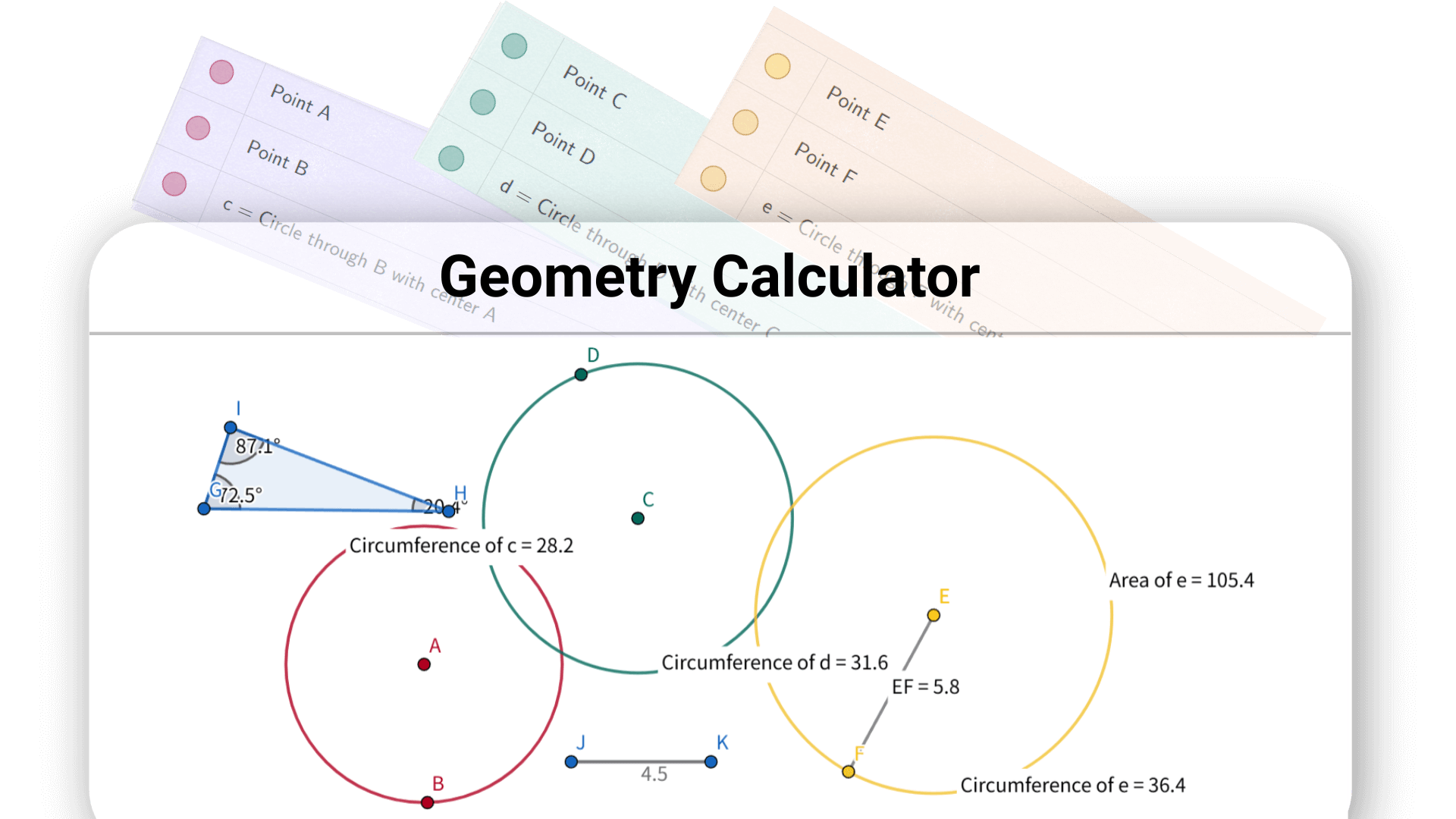
Le meilleur calculateur de géométrie de Decopy vous fait gagner un temps précieux, plus besoin de feuilleter des manuels ou de dessiner sur papier. Il vous permet de vous concentrer sur la compréhension des concepts géométriques plutôt que sur des calculs complexes.
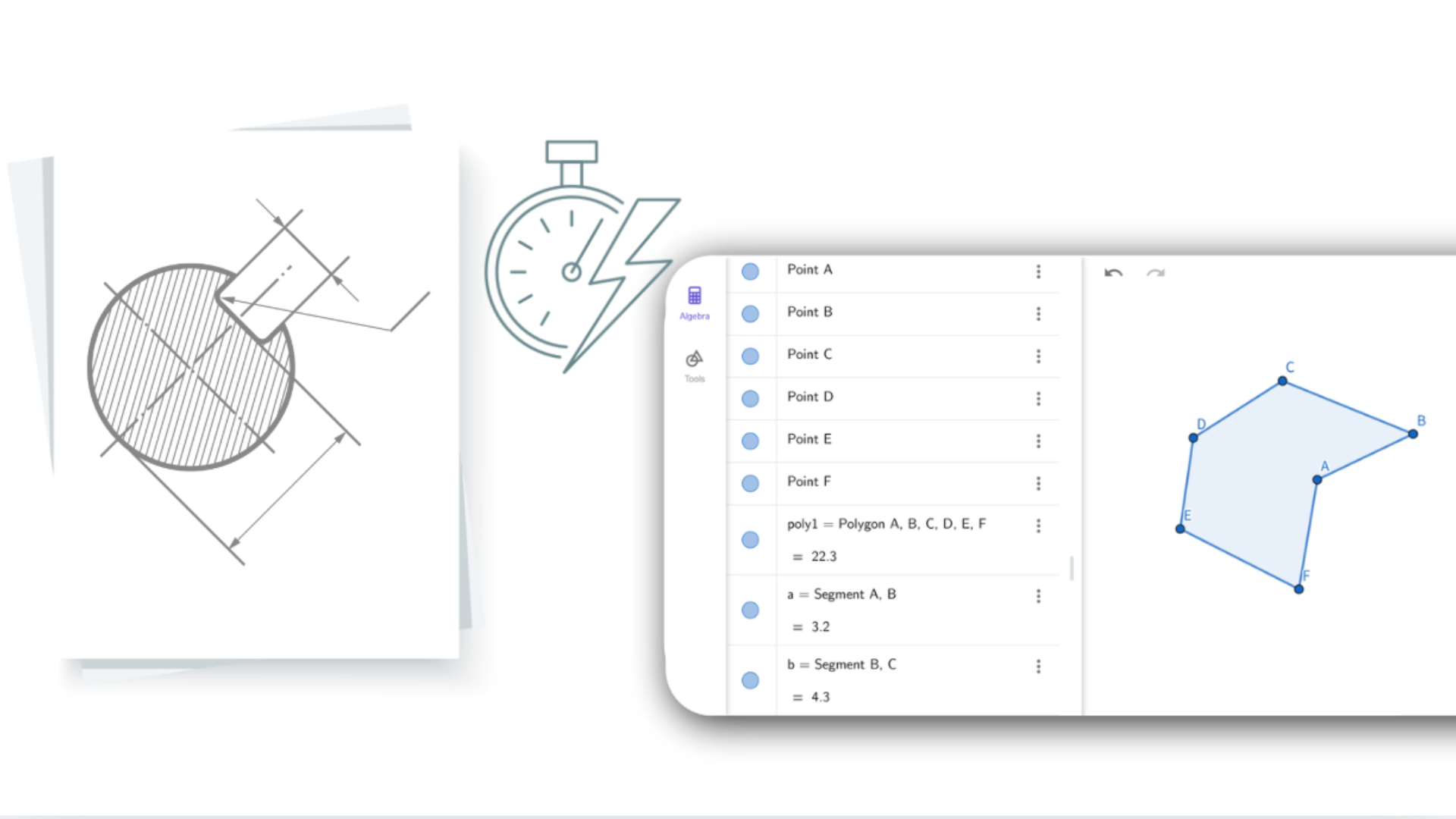
En saisissant des équations ou des coordonnées, le calculateur de géométrie affiche instantanément les formes correspondantes. Toute modification d'une figure met à jour en temps réel les expressions algébriques associées. Cette interaction dynamique relie l'algèbre à la géométrie, aidant les utilisateurs à comprendre les problèmes sous différents angles. Le calculateur de géométrie rend les mathématiques abstraites visuelles et plus faciles à appréhender.
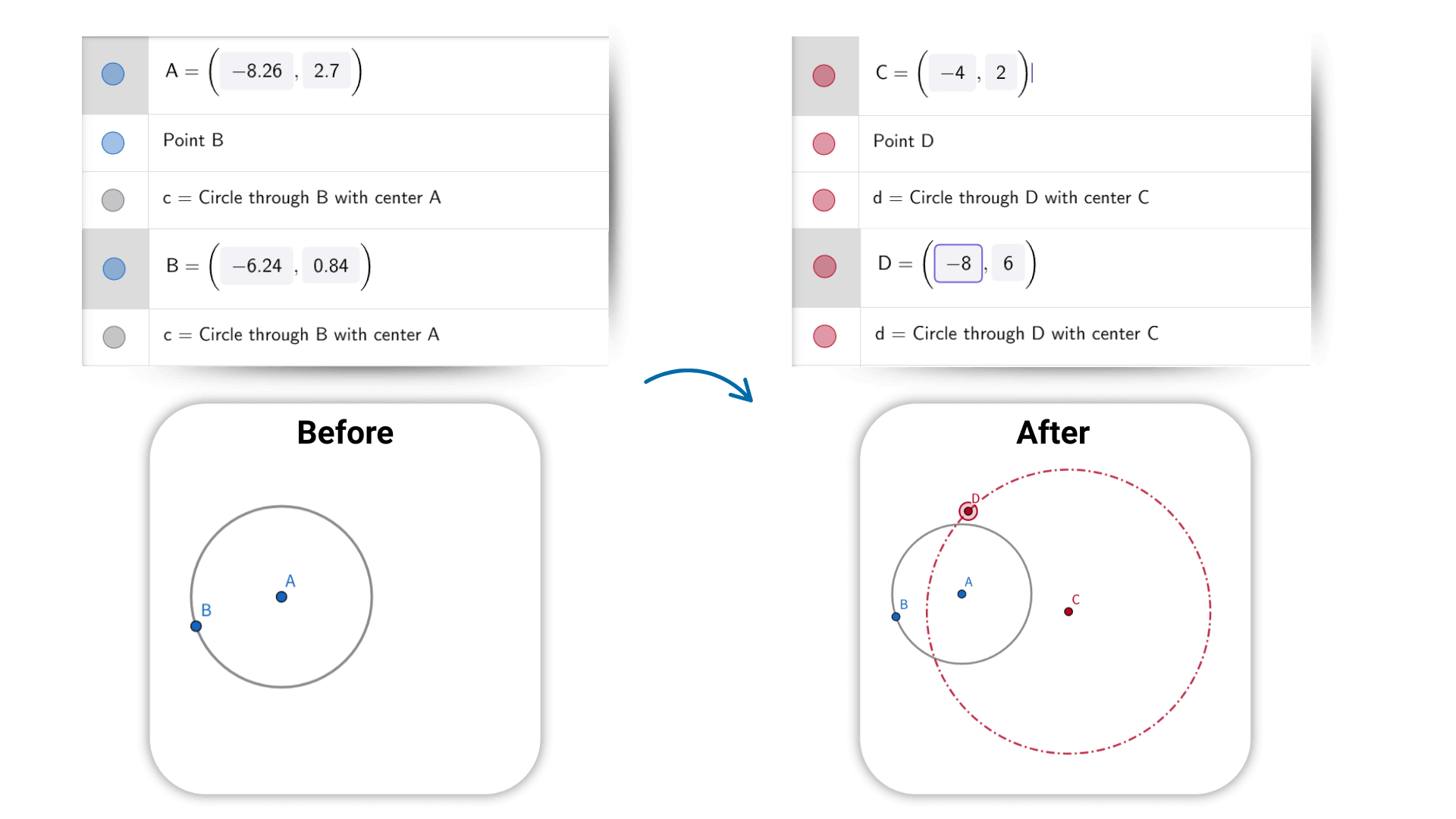
Le calculateur de géométrie prend en charge les transformations telles que la translation, la rotation et la mise à l'échelle. D'un simple geste, vous visualisez les changements de forme en temps réel. Les figures, expressions et données sont entièrement interactives : déplacer un point ou ajuster un paramètre met automatiquement à jour les relations et résultats associés. Ce calculateur en ligne vous aide à explorer les liens et comportements des objets géométriques, facilitant la compréhension de leur nature dynamique.
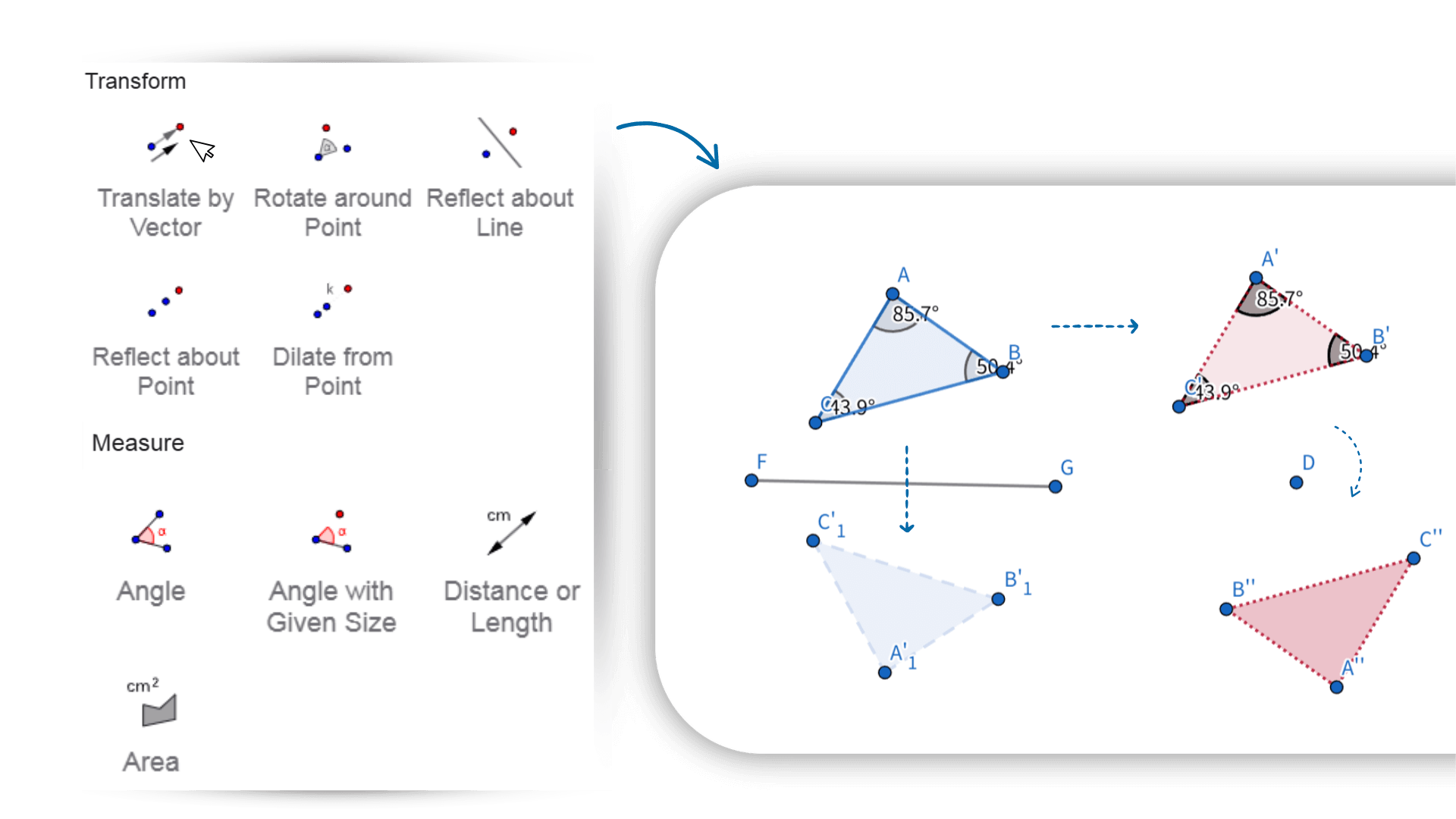
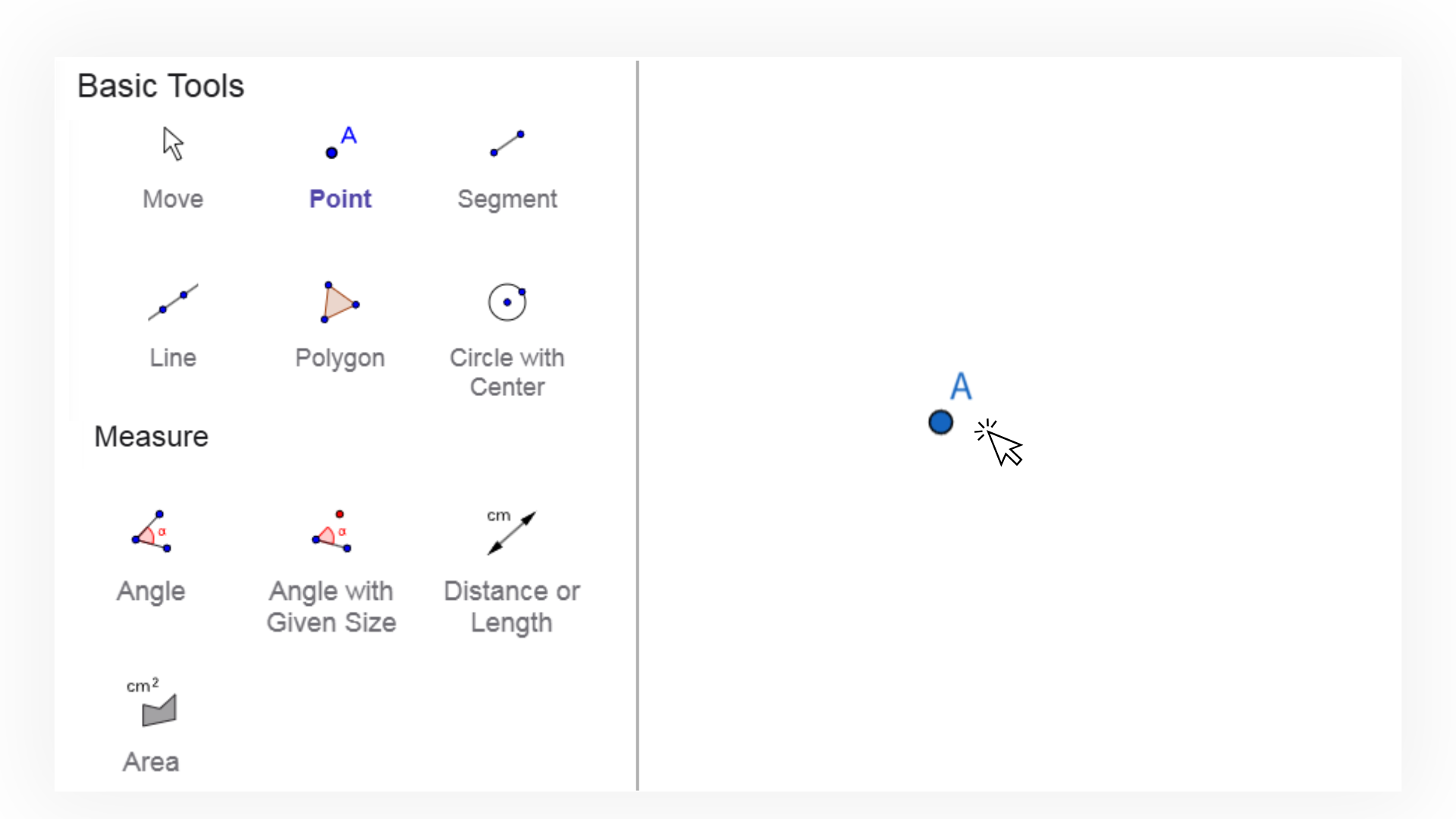
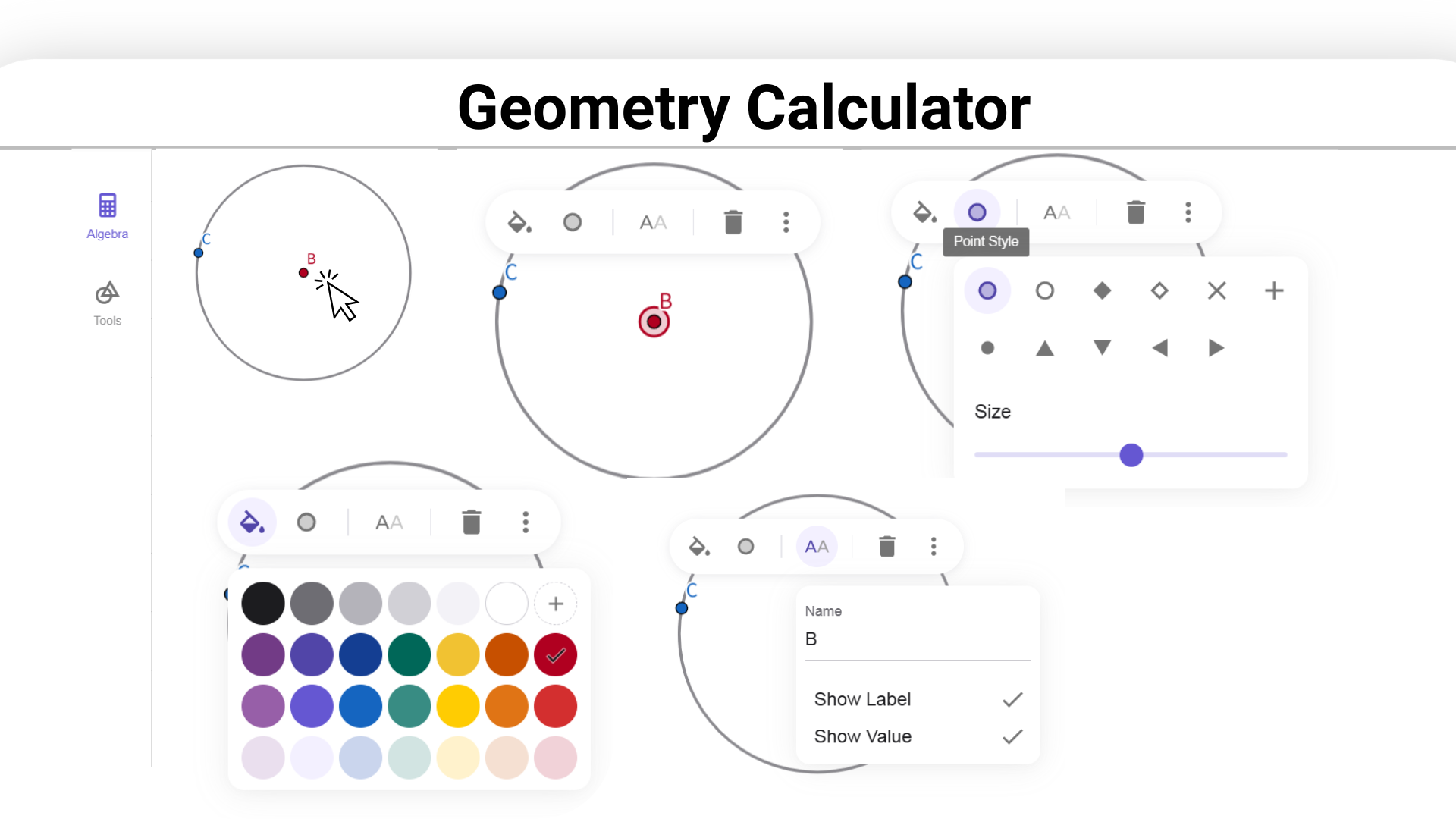
1. ![]() Sélectionnez l'outil Droite et créez une droite arbitraire
AB en cliquant deux fois dans la vue graphique.
Sélectionnez l'outil Droite et créez une droite arbitraire
AB en cliquant deux fois dans la vue graphique.
2. ![]() Créez une droite BC en utilisant à nouveau l'outil
Droite.
Créez une droite BC en utilisant à nouveau l'outil
Droite.
Astuce : Sélectionnez le point B puis
cliquez dans la vue graphique pour créer le point C.
3. ![]() Activez l'outil Droite parallèle et créez une droite
parallèle à la droite AB passant par le point C.
Activez l'outil Droite parallèle et créez une droite
parallèle à la droite AB passant par le point C.
Astuce :
Ouvrez la boîte à outils des droites spéciales, activez
l'outil Droite parallèle puis sélectionnez la droite AB puis
le point C.
4. ![]() Créez une droite parallèle à la droite BC passant par le
point A en utilisant à nouveau l'outil Droite
parallèle.
Créez une droite parallèle à la droite BC passant par le
point A en utilisant à nouveau l'outil Droite
parallèle.
5. ![]() Sélectionnez l'outil Intersection et créez le point
d'intersection D des deux droites.
Sélectionnez l'outil Intersection et créez le point
d'intersection D des deux droites.
Astuce :
Ouvrez la boîte à outils des points, activez l'outil
Intersection et cliquez directement sur le point
d'intersection.
6. ![]() Activez l'outil Polygone et créez le parallélogramme ABCD
en sélectionnant successivement tous les sommets.
Activez l'outil Polygone et créez le parallélogramme ABCD
en sélectionnant successivement tous les sommets.
Remarque :
Pour fermer votre polygone, sélectionnez à nouveau le
premier point.
7. ![]() Sélectionnez l'outil Déplacer et faites glisser les sommets
du parallélogramme pour vérifier s'il a été construit
correctement.
Sélectionnez l'outil Déplacer et faites glisser les sommets
du parallélogramme pour vérifier s'il a été construit
correctement.
1. ![]() Créez le segment AB en cliquant deux fois dans la vue
graphique.
Créez le segment AB en cliquant deux fois dans la vue
graphique.
2. ![]() Construisez un cercle de centre B passant par A en
sélectionnant ces deux points dans cet ordre.
Construisez un cercle de centre B passant par A en
sélectionnant ces deux points dans cet ordre.
3. ![]() Faites glisser les points A et B pour vérifier si le cercle
leur est bien attaché.
Faites glisser les points A et B pour vérifier si le cercle
leur est bien attaché.
4. ![]() Construisez un cercle de centre B passant par A en
sélectionnant ces deux points dans cet ordre.
Construisez un cercle de centre B passant par A en
sélectionnant ces deux points dans cet ordre.
5. ![]() Interceptez les deux cercles en les sélectionnant pour
obtenir le point C.
Interceptez les deux cercles en les sélectionnant pour
obtenir le point C.
6. ![]() Créez le polygone ABC dans le sens antihoraire. Pour fermer
le polygone, sélectionnez à nouveau le premier point.
Créez le polygone ABC dans le sens antihoraire. Pour fermer
le polygone, sélectionnez à nouveau le premier point.
7. ![]() Masquez les deux cercles en activant l'outil
Afficher/Masquer Objet et en les sélectionnant. Confirmez
votre sélection en choisissant l'outil Déplacer.
Masquez les deux cercles en activant l'outil
Afficher/Masquer Objet et en les sélectionnant. Confirmez
votre sélection en choisissant l'outil Déplacer.
8. ![]() Affichez les angles intérieurs du triangle en cliquant à
l'intérieur du triangle.
Affichez les angles intérieurs du triangle en cliquant à
l'intérieur du triangle.
Astuce : Si vous obtenez les angles extérieurs, vous
avez probablement créé le polygone dans le sens
horaire.
9. ![]() Effectuez le test de déplacement pour vérifier si la
construction est correcte.
Effectuez le test de déplacement pour vérifier si la
construction est correcte.
1. ![]() Créez un triangle ABC arbitraire en cliquant trois fois
dans la vue graphique puis en sélectionnant à nouveau le
premier point créé.
Créez un triangle ABC arbitraire en cliquant trois fois
dans la vue graphique puis en sélectionnant à nouveau le
premier point créé.
2. ![]() Construisez la médiatrice de chaque côté du triangle.
Construisez la médiatrice de chaque côté du triangle.
Astuce :
L'outil Médiatrice peut être appliqué à un segment
existant.
3. ![]() Créez le point d'intersection D de deux des médiatrices.
Créez le point d'intersection D de deux des médiatrices.
Astuce :
L'outil Intersection peut être appliqué à l'intersection de
trois droites ou en sélectionnant successivement deux des
trois médiatrices.
4. ![]() Construisez un cercle de centre D passant par un des
sommets du triangle ABC en sélectionnant d'abord D puis un
des sommets du triangle.
Construisez un cercle de centre D passant par un des
sommets du triangle ABC en sélectionnant d'abord D puis un
des sommets du triangle.
5. ![]() Effectuez le test de déplacement en bougeant les sommets du
triangle pour vérifier si votre construction est
correcte.
Effectuez le test de déplacement en bougeant les sommets du
triangle pour vérifier si votre construction est
correcte.
1. ![]() Assurez-vous d'avoir enregistré l'image de la fleur jaune
sur votre ordinateur avant de commencer la
construction.
Assurez-vous d'avoir enregistré l'image de la fleur jaune
sur votre ordinateur avant de commencer la
construction.
2. ![]() Créez un nouveau point A.
Créez un nouveau point A.
3. ![]() Construisez un axe de symétrie en passant par deux nouveaux
points en cliquant deux fois dans la vue graphique.
Construisez un axe de symétrie en passant par deux nouveaux
points en cliquant deux fois dans la vue graphique.
4. ![]() Effectuez la symétrie du point A par rapport à la droite
pour obtenir son image A’.
Effectuez la symétrie du point A par rapport à la droite
pour obtenir son image A’.
Astuce : Sélectionnez
d'abord le point A puis la droite.
5. ![]() Créez un segment entre le point A et son image A’ en
sélectionnant les deux points.
Créez un segment entre le point A et son image A’ en
sélectionnant les deux points.
6. ![]() Activez la trace pour les points A et A′.
Activez la trace pour les points A et A′.
Astuce :
Faites un clic droit (MacOS : Ctrl-clic) sur un point et
sélectionnez Afficher la trace.
Remarque : À
chaque déplacement du point A, une trace apparaît dans la
vue graphique.
7. ![]() Faites glisser le point A pour dessiner une trace.
Faites glisser le point A pour dessiner une trace.
Astuce :
L'option Rafraîchir les vues dans le menu Vue efface toutes
les traces.
1. ![]() Assurez-vous d'avoir enregistré l'image du coucher de
soleil sur votre ordinateur avant de commencer la
construction.
Assurez-vous d'avoir enregistré l'image du coucher de
soleil sur votre ordinateur avant de commencer la
construction.
2. ![]() Insérez l'image du coucher de soleil dans la partie gauche
de la vue graphique à l'aide de l'outil Image.
Insérez l'image du coucher de soleil dans la partie gauche
de la vue graphique à l'aide de l'outil Image.
Remarque : Le premier point d'angle A et le second
point d'angle B de l'image sont créés automatiquement.
3. ![]() Déplacez le point A dans le coin inférieur gauche de
l'image et observez comment cela affecte l'image.
Déplacez le point A dans le coin inférieur gauche de
l'image et observez comment cela affecte l'image.
4. ![]() Supprimez le point B à l'aide de l'outil Supprimer.
Supprimez le point B à l'aide de l'outil Supprimer.
5. ![]() Créez un nouveau point B en saisissant B = A + (3, 0) dans
la barre de saisie.
Créez un nouveau point B en saisissant B = A + (3, 0) dans
la barre de saisie.
Astuce : N'oubliez pas
d'appuyer sur Entrée après votre saisie.
6. ![]() Définissez le nouveau point B comme DEUXIÈME point d'angle
de l'image pour changer sa largeur à 3 cm.
Définissez le nouveau point B comme DEUXIÈME point d'angle
de l'image pour changer sa largeur à 3 cm.
Astuce : Ouvrez les paramètres de l'image et
sélectionnez l'onglet Position.
7. ![]() Créez une droite verticale passant par deux points au
centre de la vue graphique à l'aide de l'outil Droite.
Créez une droite verticale passant par deux points au
centre de la vue graphique à l'aide de l'outil Droite.
8. ![]() Effectuez la symétrie de l'image par rapport à la droite à
l'aide de l'outil Symétrie axiale en sélectionnant d'abord
l'image puis la droite.
Effectuez la symétrie de l'image par rapport à la droite à
l'aide de l'outil Symétrie axiale en sélectionnant d'abord
l'image puis la droite.
9. ![]() Vous pouvez réduire l'opacité de l'image pour mieux la
distinguer de l'originale (Paramètres de l'image, onglet
Couleur).
Vous pouvez réduire l'opacité de l'image pour mieux la
distinguer de l'originale (Paramètres de l'image, onglet
Couleur).
1. ![]() Assurez-vous d'avoir enregistré l'image de Bart Simpson sur
votre ordinateur avant de commencer la construction.
Assurez-vous d'avoir enregistré l'image de Bart Simpson sur
votre ordinateur avant de commencer la construction.
2. ![]() Sélectionnez l'outil Image pour insérer l'image de Bart.
Sélectionnez l'outil Image pour insérer l'image de Bart.
Astuce :
Le calculateur de géométrie créera automatiquement le
premier et le second point d'angle A et B de l'image.
3. ![]() Faites glisser le premier point d'angle A de l'image à la
position (1, 1).
Faites glisser le premier point d'angle A de l'image à la
position (1, 1).
4. ![]() Créez le point D = (1, 3.9).
Créez le point D = (1, 3.9).
Astuce : Vous
pouvez saisir directement les coordonnées dans la barre de
saisie.
5. ![]() Définissez le point D comme QUATRIÈME point d'angle de
l'image.
Définissez le point D comme QUATRIÈME point d'angle de
l'image.
Astuce : Ouvrez les paramètres de
l'image et sélectionnez l'onglet Position.
6. ![]() Créez un triangle rigide ABD à l'aide de l'outil Polygone
rigide.
Créez un triangle rigide ABD à l'aide de l'outil Polygone
rigide.
Astuce : Fermez le polygone en
sélectionnant à nouveau le premier point. Le polygone
résultant gardera sa forme lors des déplacements. Il peut
être déplacé ou tourné en faisant glisser deux
sommets.
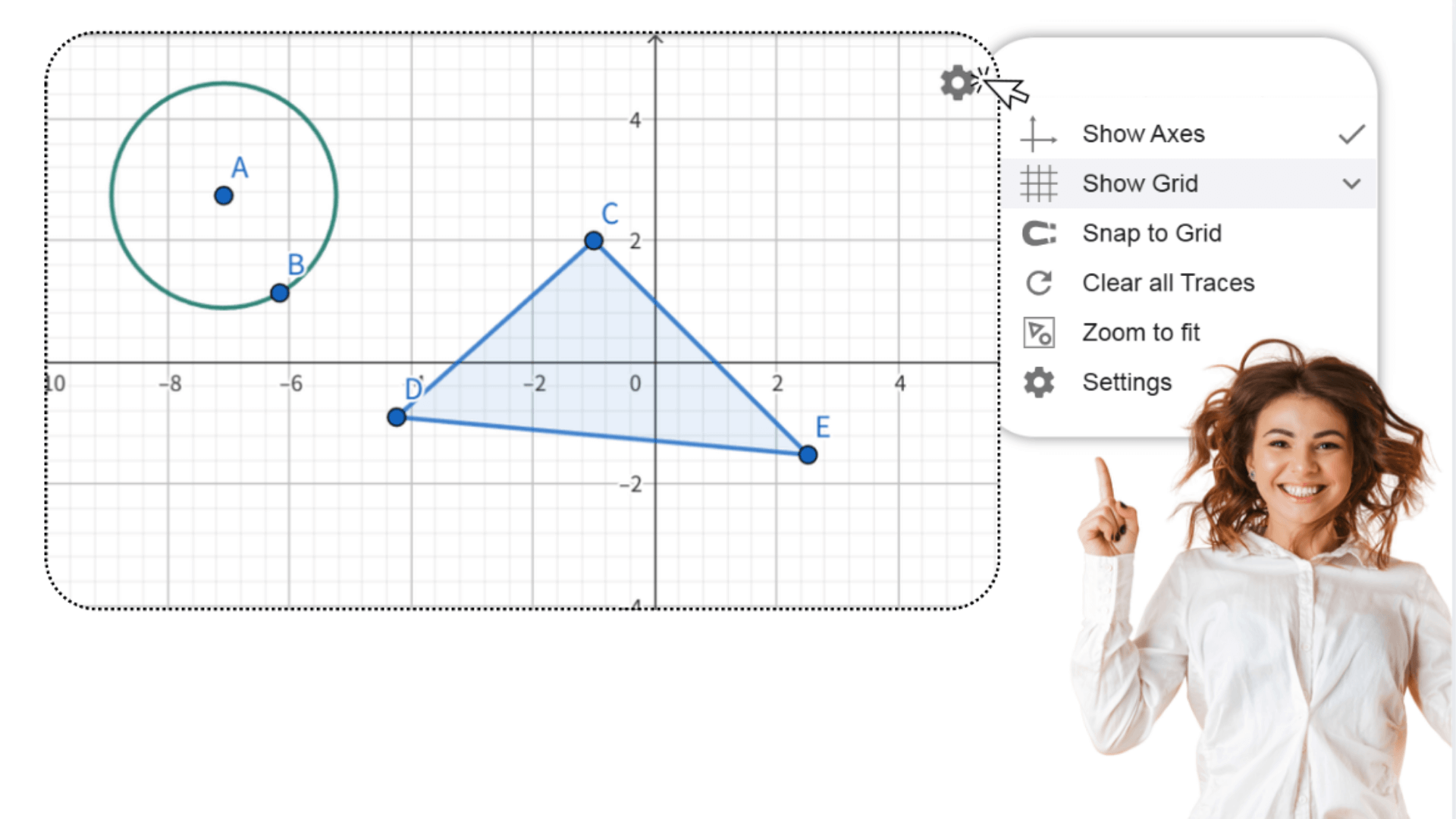
1. ![]() Créez un triangle ABC arbitraire dans le premier quadrant,
en plaçant les sommets sur les points de la grille.
Créez un triangle ABC arbitraire dans le premier quadrant,
en plaçant les sommets sur les points de la grille.
2. ![]() Créez un nouveau point D à l'origine du système de
coordonnées.
Créez un nouveau point D à l'origine du système de
coordonnées.
3. ![]() Renommez le point D en O.
Renommez le point D en O.
Astuce : Sélectionnez
le point D et tapez simplement O pour ouvrir la boîte de
dialogue Renommer.
4. ![]() Créez un curseur pour l'angle α.
Créez un curseur pour l'angle α.
Astuce : Dans
la fenêtre de dialogue du curseur, cochez Angle et
définissez l'incrément à 90°. Assurez-vous de ne pas
supprimer le symbole °.
5. ![]() Utilisez l'outil Rotation autour d'un point pour faire
tourner le triangle ABC autour du point O d'un angle α.
Utilisez l'outil Rotation autour d'un point pour faire
tourner le triangle ABC autour du point O d'un angle α.
Astuce :
Activez l'outil et sélectionnez le triangle avant de
sélectionner le centre de rotation. Dans la boîte de
dialogue qui apparaît, saisissez α comme angle via le
clavier virtuel et choisissez la rotation dans le sens
antihoraire.
6. ![]() Créez les segments AO et A’O.
Créez les segments AO et A’O.
7. ![]() Créez l'angle AOA’.
Créez l'angle AOA’.
Astuce : Sélectionnez les
points dans le sens antihoraire.
8. ![]() Masquez l'étiquette de l'angle AOA’.
Masquez l'étiquette de l'angle AOA’.
9. ![]() Déplacez le curseur et explorez l'image du triangle.
Déplacez le curseur et explorez l'image du triangle.
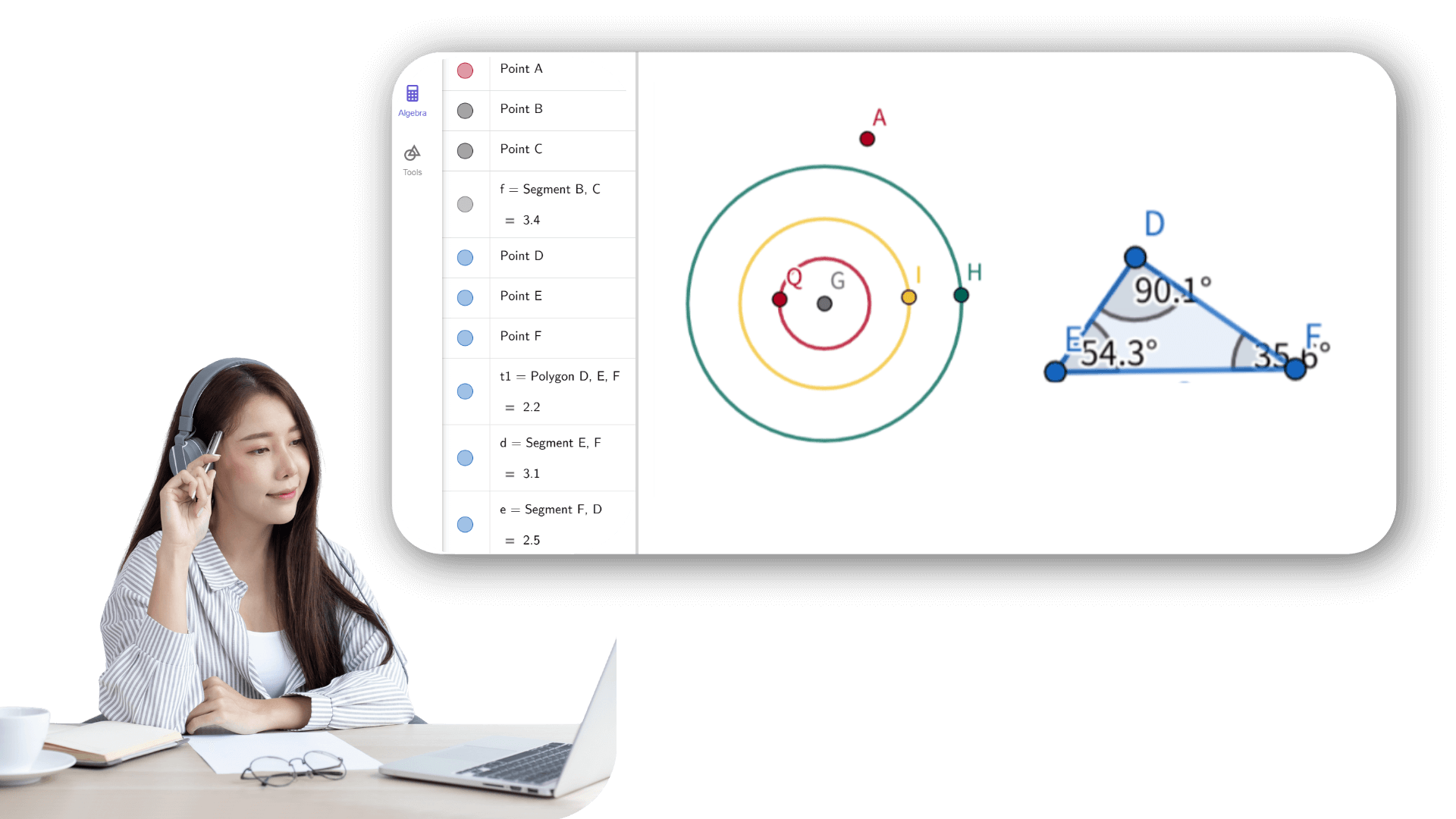
1. ![]() Créez les curseurs a, b et c pour les longueurs des côtés
du triangle avec un intervalle de 0 à 10 et un incrément de
0,5 chacun.
Créez les curseurs a, b et c pour les longueurs des côtés
du triangle avec un intervalle de 0 à 10 et un incrément de
0,5 chacun.
2. ![]() Réglez les valeurs des curseurs à a = 8, b = 6,5 et c =
10.
Réglez les valeurs des curseurs à a = 8, b = 6,5 et c =
10.
3. ![]() Créez le segment f de longueur c.
Créez le segment f de longueur c.
Astuce : Les
points A et B sont les extrémités du segment.
4. ![]() Créez un cercle d de centre A et de rayon b.
Créez un cercle d de centre A et de rayon b.
5. ![]() Créez un cercle e de centre B et de rayon a.
Créez un cercle e de centre B et de rayon a.
6. ![]() Construisez le point d'intersection C des deux cercles e et
f.
Construisez le point d'intersection C des deux cercles e et
f.
7. ![]() Créez le triangle ABC.
Créez le triangle ABC.
8. ![]() Créez les angles intérieurs α, β et γ du triangle
ABC.
Créez les angles intérieurs α, β et γ du triangle
ABC.
9. ![]() Créez un point D sur le cercle d.
Créez un point D sur le cercle d.
10. ![]() Créez le segment g entre les points A et D.
Créez le segment g entre les points A et D.
11. ![]() Construisez le milieu E du segment g.
Construisez le milieu E du segment g.
12. ![]() Saisissez texte1 : b et attachez-le au point E.
Saisissez texte1 : b et attachez-le au point E.
Astuce :
Après avoir sélectionné l'outil Texte, cliquez sur le point
E. Ouvrez Avancé et sélectionnez b dans l'onglet
Objets.
13. ![]() Créez un point F sur le cercle e.
Créez un point F sur le cercle e.
14. ![]() Créez le segment h entre les points B et F.
Créez le segment h entre les points B et F.
15. ![]() Construisez le milieu G du segment h.
Construisez le milieu G du segment h.
16. ![]() Saisissez texte2 : a et attachez-le au point G.
Saisissez texte2 : a et attachez-le au point G.
17. ![]() Masquez les points D, E, F et G à l'aide de l'outil
Afficher/Masquer Objet.
Masquez les points D, E, F et G à l'aide de l'outil
Afficher/Masquer Objet.
18. ![]() Améliorez votre construction à l'aide de la barre de style
et harmonisez les couleurs des objets correspondants.
Améliorez votre construction à l'aide de la barre de style
et harmonisez les couleurs des objets correspondants.
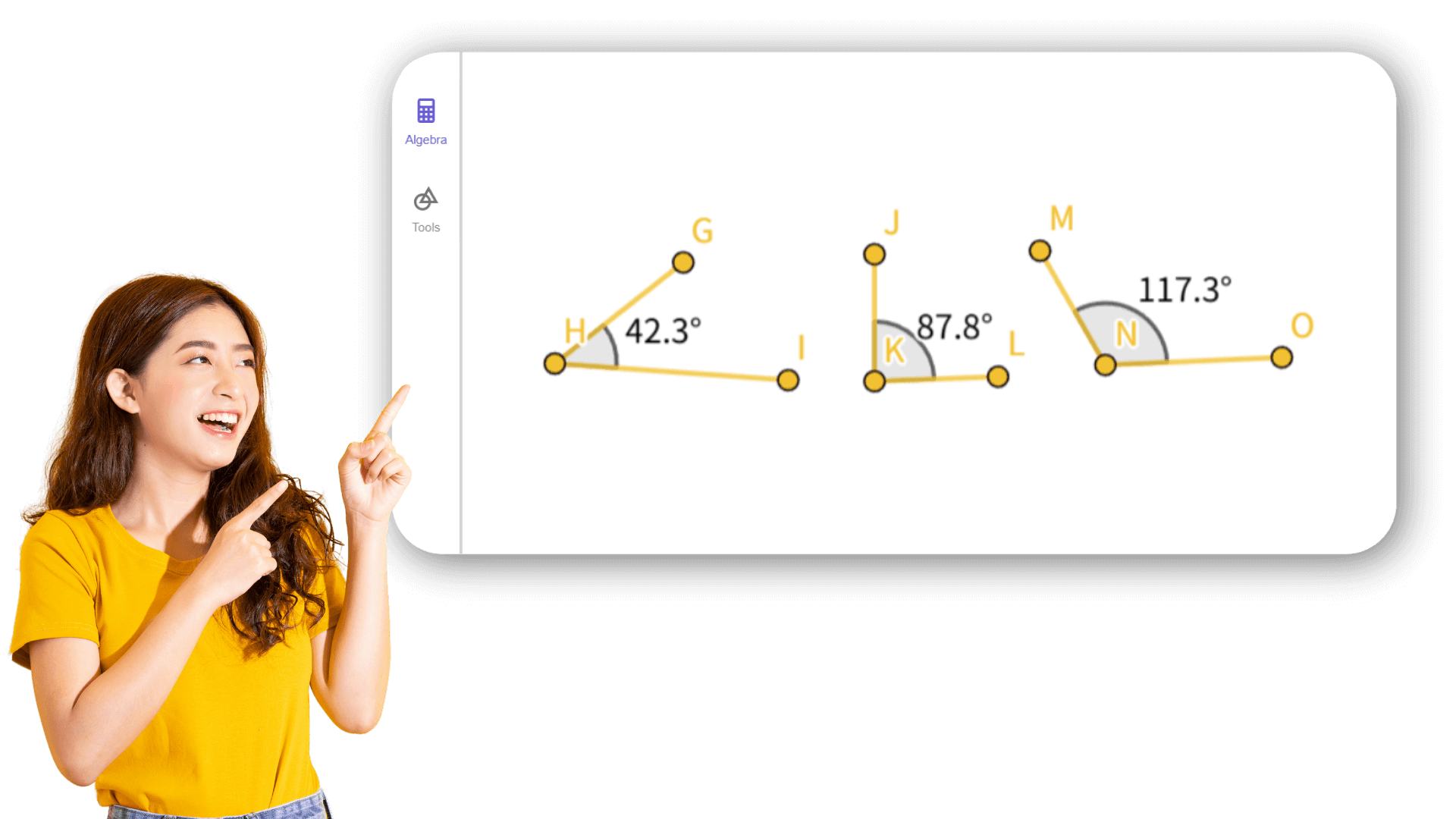
1. ![]() Créez un triangle ABC dans le sens antihoraire.
Créez un triangle ABC dans le sens antihoraire.
2. ![]() Créez les angles α, β et γ du triangle ABC.
Créez les angles α, β et γ du triangle ABC.
3. ![]() Créez un curseur pour l'angle δ avec un intervalle de 0° à
180° et un incrément de 10°.
Créez un curseur pour l'angle δ avec un intervalle de 0° à
180° et un incrément de 10°.
4. ![]() Créez un curseur pour l'angle ε avec un intervalle de 0° à
180° et un incrément de 10°.
Créez un curseur pour l'angle ε avec un intervalle de 0° à
180° et un incrément de 10°.
5. ![]() Créez le milieu D du segment AC et le milieu E du segment
AB.
Créez le milieu D du segment AC et le milieu E du segment
AB.
6. ![]() Faites tourner le triangle autour du point D d'un angle δ
(sens horaire).
Faites tourner le triangle autour du point D d'un angle δ
(sens horaire).
Astuce : Saisissez δ à l'aide du
clavier virtuel.
7. ![]() Faites tourner le triangle autour du point E d'un angle ε
(sens antihoraire).
Faites tourner le triangle autour du point E d'un angle ε
(sens antihoraire).
Astuce : Saisissez ε à
l'aide du clavier virtuel.
8. ![]() Déplacez les deux curseurs δ et ε pour afficher 180°.
Déplacez les deux curseurs δ et ε pour afficher 180°.
9. ![]() Créez l'angle ζ en utilisant les points A’C’B’.
Créez l'angle ζ en utilisant les points A’C’B’.
Astuce :
Pour être sûr de sélectionner les bons sommets, modifiez
l'angle δ ou utilisez la commande
angle(A’, C’, B’).
10. ![]() Créez l'angle η en utilisant les points C'1B'1A'1.
Créez l'angle η en utilisant les points C'1B'1A'1.
Astuce :
Pour être sûr de sélectionner les bons sommets, modifiez
l'angle ε avant ou utilisez la commande
angle(C'1, B'1, A'1).
11. ![]() Améliorez votre construction à l'aide de la barre de
style.
Améliorez votre construction à l'aide de la barre de
style.
Astuce : Les angles congruents doivent
avoir la même couleur.
12. ![]() Créez un texte dynamique affichant les angles intérieurs et
leurs valeurs (par exemple, saisissez α = et sélectionnez α
dans la liste des objets de l'onglet Avancé).
Créez un texte dynamique affichant les angles intérieurs et
leurs valeurs (par exemple, saisissez α = et sélectionnez α
dans la liste des objets de l'onglet Avancé).
13. ![]() Calculez la somme des angles en saisissant
Calculez la somme des angles en saisissant
somme = α + β + γ dans la barre de
saisie.
14. ![]() Insérez la somme des angles comme texte dynamique :
Insérez la somme des angles comme texte dynamique :
α + β + γ = et sélectionnez somme dans la liste
des objets de l'onglet.
15. ![]() Harmonisez les couleurs des angles et des textes
correspondants à l'aide de la barre de style.
Harmonisez les couleurs des angles et des textes
correspondants à l'aide de la barre de style.
16. ![]() Fixez tous les textes qui ne doivent pas être déplacés à
l'aide de la barre de style.
Fixez tous les textes qui ne doivent pas être déplacés à
l'aide de la barre de style.
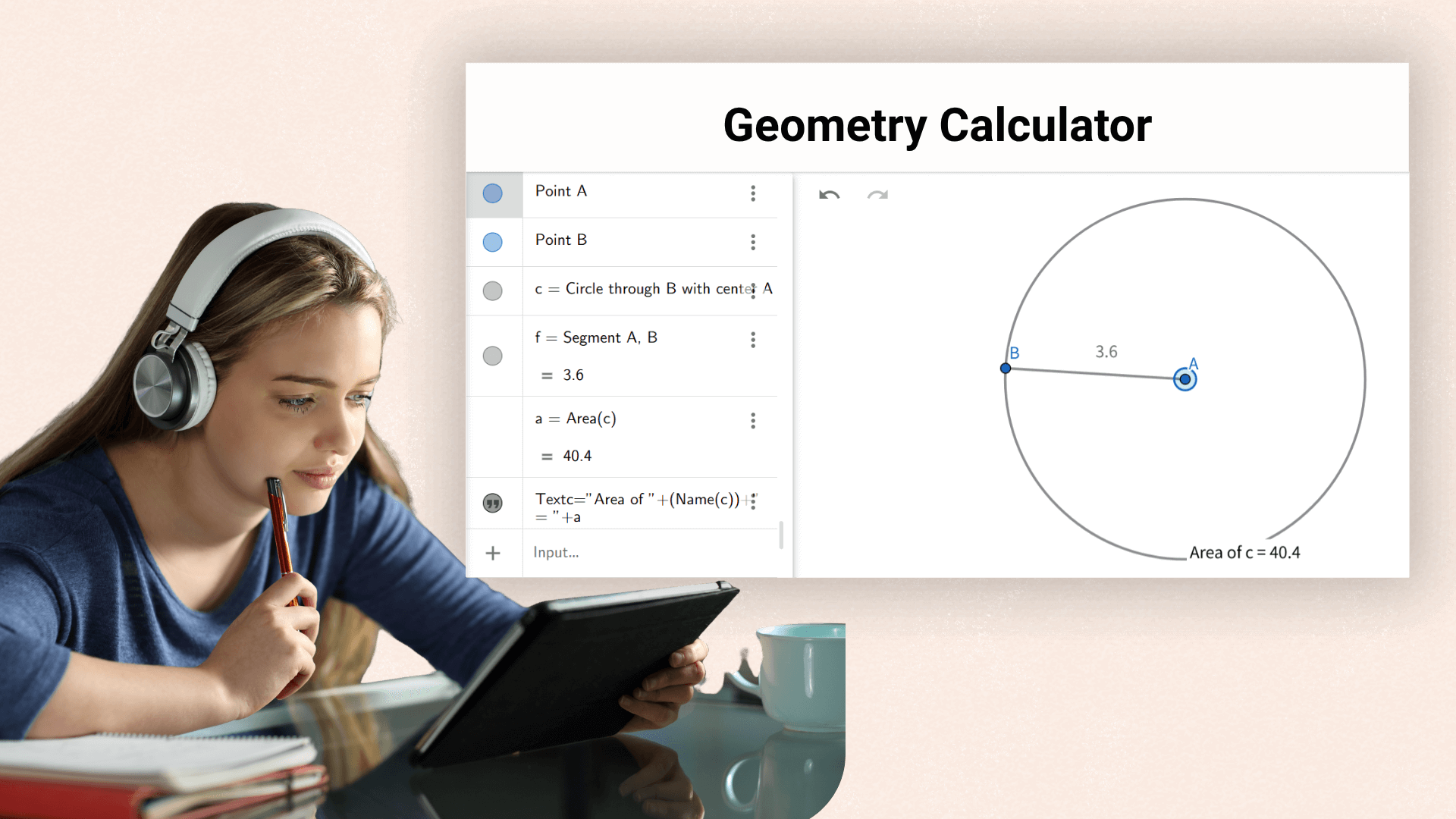
Aide les élèves à vérifier rapidement des formules et à résoudre des problèmes en cours de géométrie, améliorant ainsi l'efficacité de l'apprentissage.
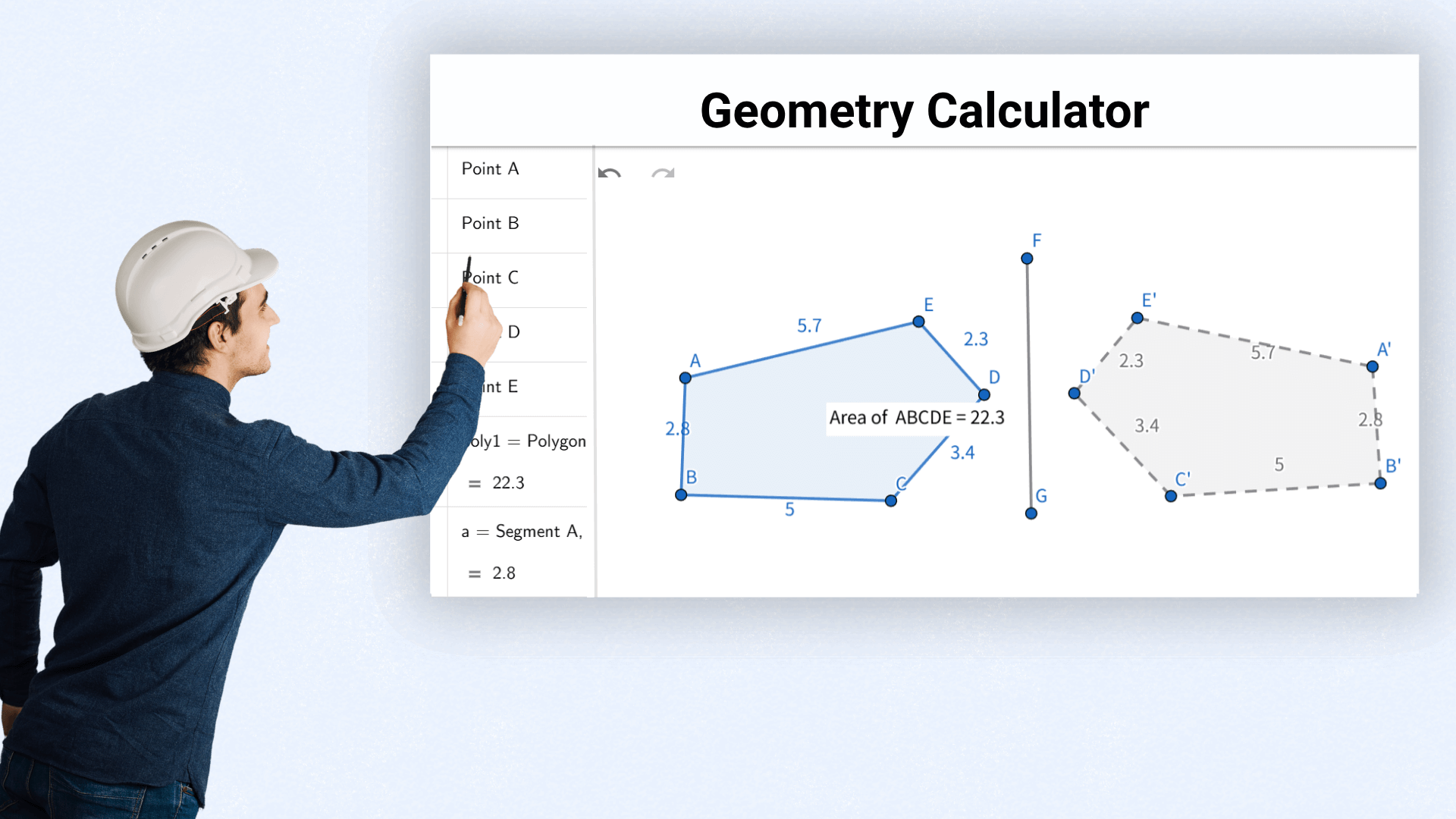
Les architectes calculent l'aire et le volume pour évaluer la faisabilité et optimiser l'agencement des espaces.

Les amateurs utilisent le calculateur de géométrie pour mesurer précisément les matériaux lors de la création de projets géométriques.
Explorez le lien entre l'algèbre et la géométrie, approfondissez la compréhension des concepts mathématiques et utilisez le calculateur pour réaliser devoirs et projets.
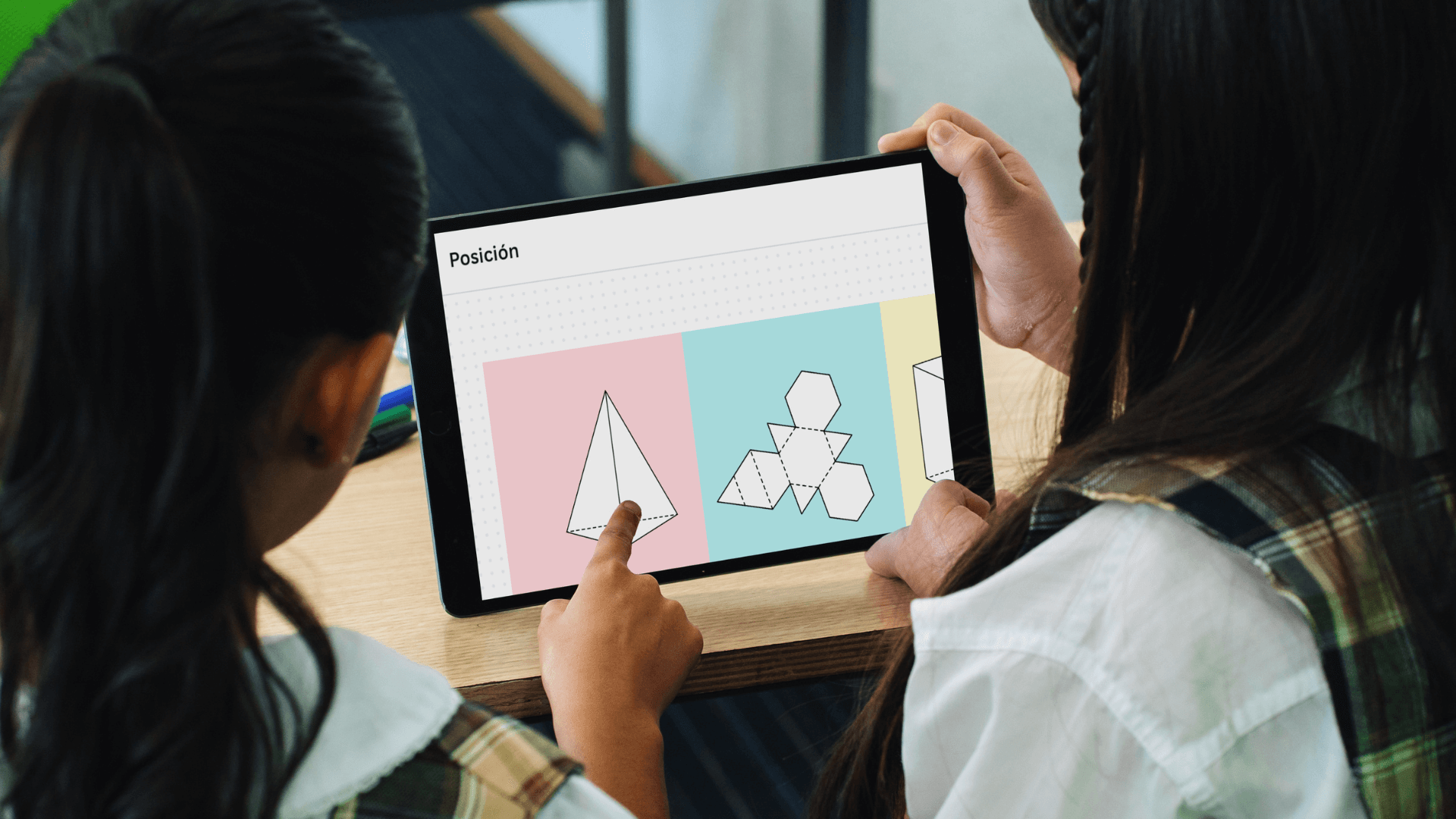
Les enseignants utilisent le calculateur pour présenter visuellement les concepts géométriques lors de la préparation des cours et des démonstrations, améliorant ainsi l'efficacité pédagogique.
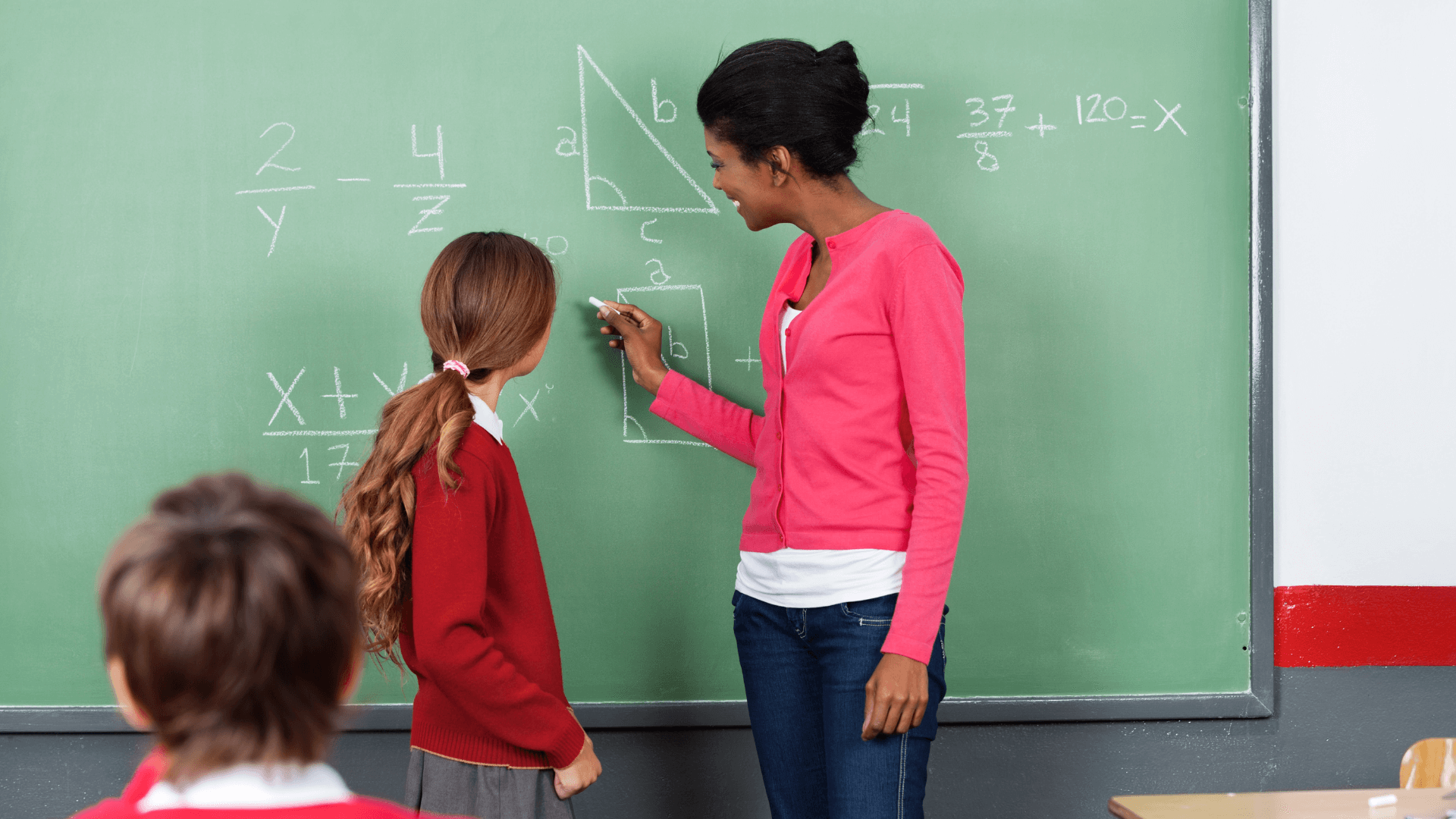
Les ingénieurs s'appuient sur le calculateur pour calculer précisément angles et longueurs dans les conceptions structurelles ou mécaniques, réduisant les erreurs de calcul manuel.

Les amateurs utilisent le calculateur pour garantir des mesures précises lors de la création d'objets géométriques.
Utilisez le calculateur pour esquisser et ajuster rapidement des concepts de design, comprenant mieux les relations spatiales avant de passer à des outils CAO détaillés.

Les chercheurs visualisent des structures complexes et analysent des données grâce aux fonctions de dessin et de calcul du calculateur, soutenant l'exploration scientifique.
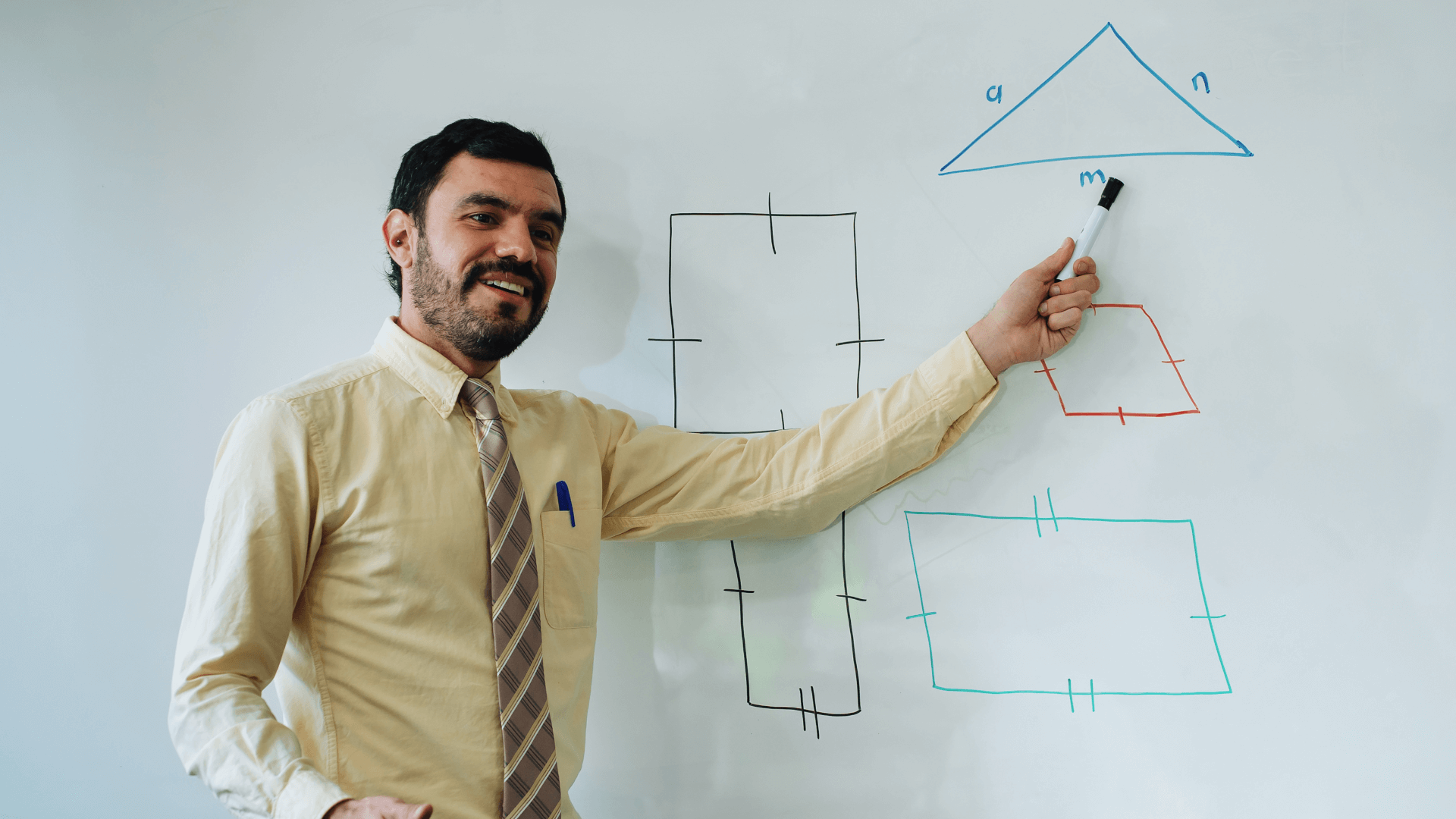
Utilise des algorithmes avancés pour garantir des résultats géométriques de haute précision.
Interface simple et intuitive avec un flux de travail clair — aucune formation complexe requise, même pour les nouveaux utilisateurs.
Intègre de nombreux outils et fonctionnalités pour répondre à tous les besoins de calcul géométrique en un seul endroit.
Performance rapide et fonctionnement fluide, même avec de grandes quantités de données ou des formules complexes.
Dessinez précisément des formes en contrôlant leur taille et leurs propriétés, offrant une base visuelle fiable pour l'analyse et la recherche.
Toutes les fonctionnalités du calculateur de géométrie en ligne sont gratuites, rendant des outils géométriques de qualité accessibles à tous.
Oui, il est entièrement gratuit. Les utilisateurs ont accès à toutes les fonctionnalités sans aucun coût.
Ouvrez notre site, sélectionnez "Nouvelle géométrie", puis cliquez sur des outils comme "Point", "Segment" ou "Cercle" pour placer des formes dans la zone de dessin.
Il est largement utilisé dans l'enseignement des mathématiques et peut aussi aider à enseigner la géométrie, l'algèbre et le calcul.
Dessinez ou importez la forme, sélectionnez l'objet à mesurer, puis choisissez des propriétés comme la distance, la longueur, l'angle, le périmètre ou l'aire. Les résultats s'affichent dans la zone de dessin ou d'algèbre.
Oui. Le calculateur de géométrie est facile à utiliser avec une interface intuitive — parfait pour les débutants.
Sélectionnez la forme et utilisez le menu contextuel ou le panneau de propriétés pour modifier son apparence, y compris la couleur, le style de ligne et le remplissage.
Notre calculateur de géométrie utilise des algorithmes avancés pour fournir des résultats précis et fiables.
Il aide les élèves à explorer le lien entre l'algèbre et la géométrie, et les soutient dans la réalisation de devoirs et de projets de recherche plus efficacement.