Étudiants
La calculatrice graphique bénéficie aux étudiants du primaire à l'université. Elle les aide à comprendre les concepts mathématiques et à cultiver des compétences de résolution de problèmes.
Un calculateur graphique peut résoudre des équations et dessiner des graphiques de fonctions, vous aidant à comprendre de manière intuitive et précise les modèles changeants des fonctions.
La calculatrice graphique est un outil de dessin puissant et technologiquement avancé qui nous aide à tracer des graphiques de fonctions, à effectuer des calculs complexes et à mener des analyses de données. En ajustant les paramètres pour affecter la transformation des graphiques, l'apprentissage et la recherche mathématiques deviennent plus intuitifs, efficaces et intéressants.
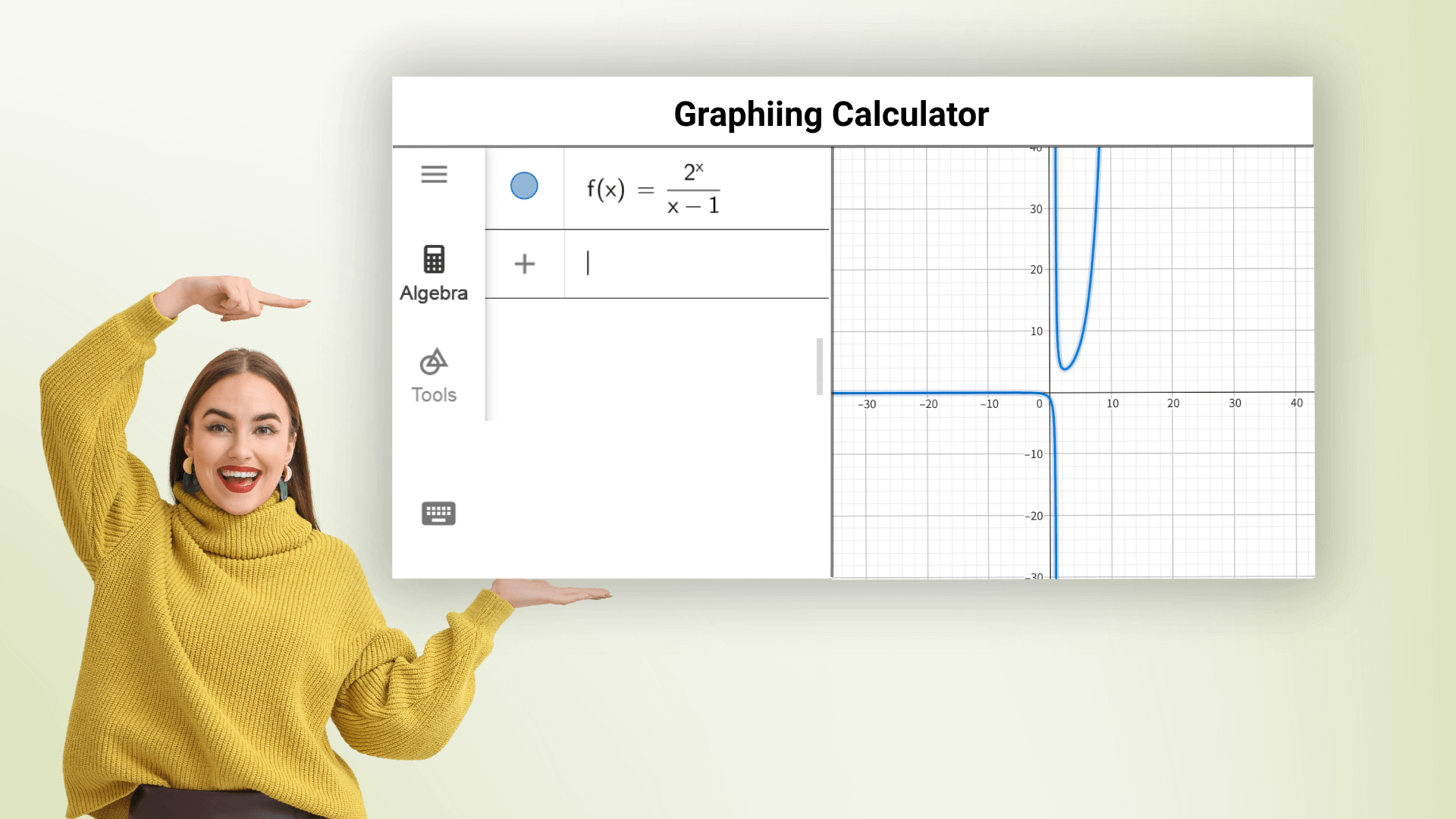
La calculatrice graphique peut tracer divers graphiques de fonctions, y compris des fonctions linéaires, paraboliques, trigonométriques et logarithmiques, et elle peut tracer plusieurs équations à la fois dans différentes couleurs. Il suffit d'entrer l'expression de la fonction pour obtenir rapidement un graphique précis et observer les tendances et les caractéristiques de la fonction. La calculatrice graphique en ligne aide tout le monde à maîtriser les mathématiques et à éviter les calculs complexes.
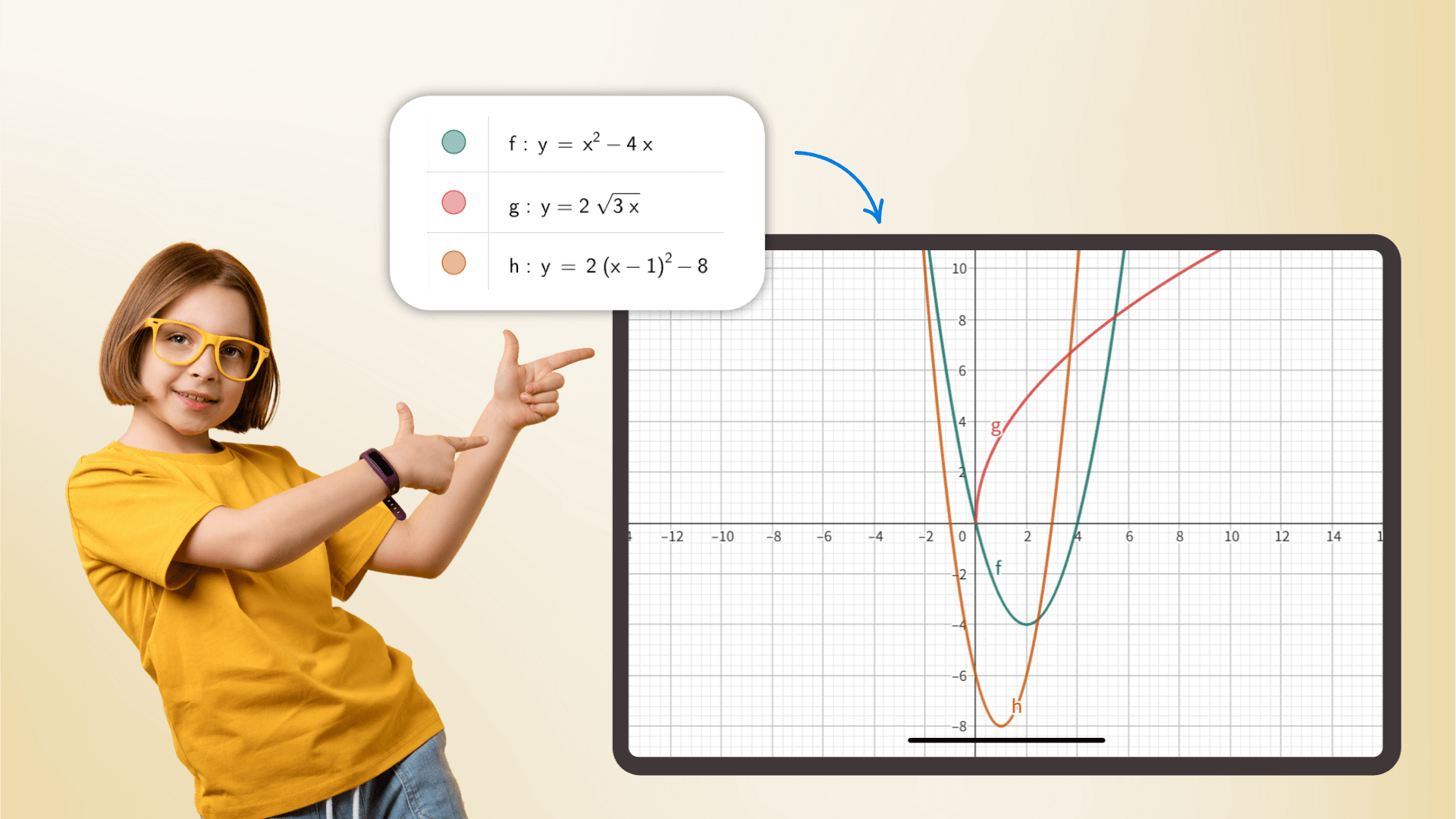
En tant que calculatrice scientifique, elle gère tout, de l'arithmétique de base aux mathématiques avancées, au calcul, aux statistiques de probabilité et plus encore. Avec des calculs précis, elle sert d'assistant indispensable pour les étudiants et les chercheurs, améliorant l'efficacité dans les contextes académiques et professionnels.
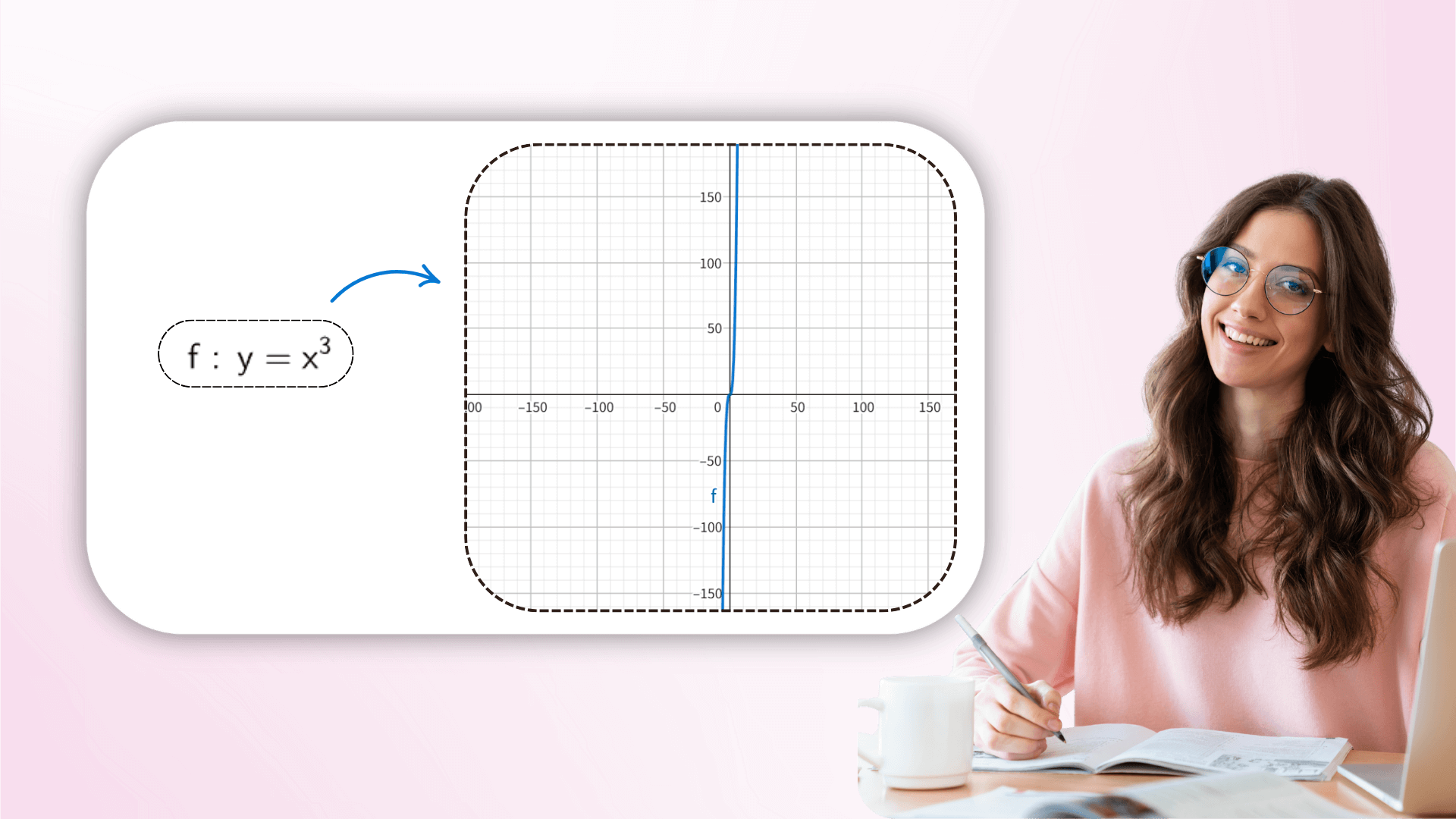
En ajustant les valeurs des paramètres en temps réel, les utilisateurs peuvent observer la transformation dynamique de l'image pour comprendre comment les coefficients affectent la géométrie de la fonction, de la translation linéaire aux transformations complexes, en liant les formules abstraites à la vision. Cette exploration interactive peut approfondir la compréhension des équations mathématiques.
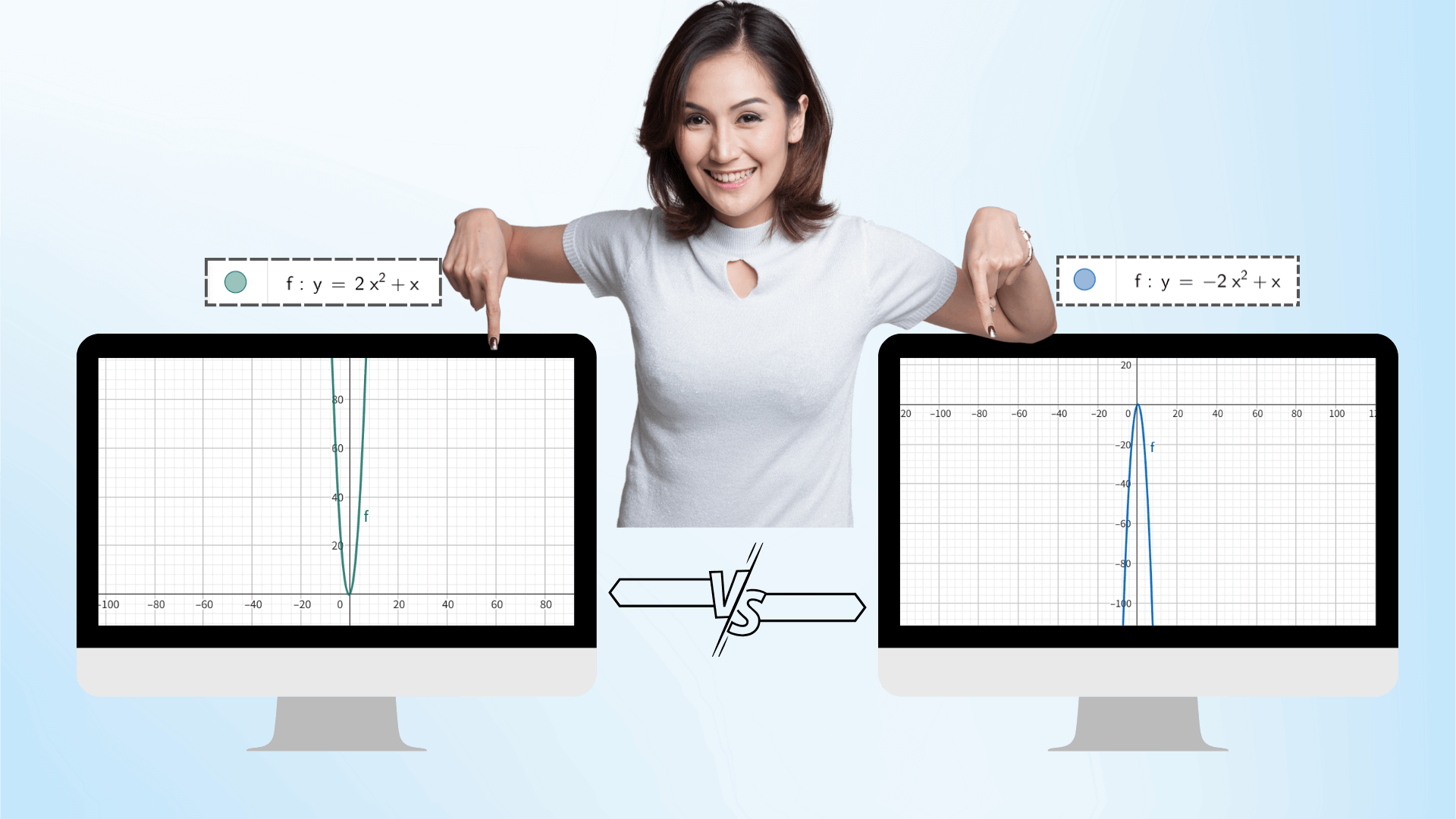
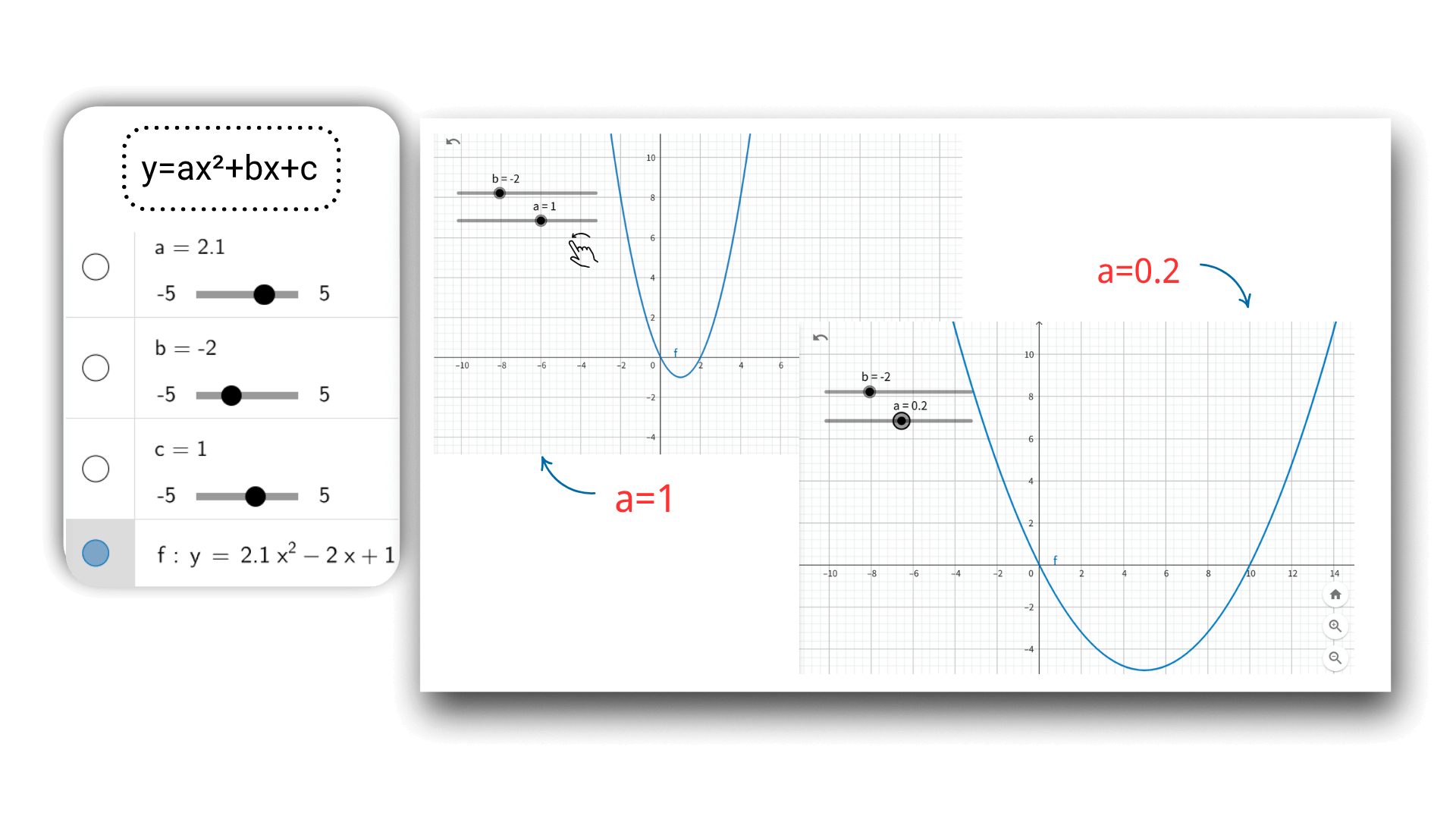
En utilisant la technologie de graphique AI, après avoir entré la fonction, vous pouvez ajuster dynamiquement les paramètres via le curseur, tels que a, b, c d'une fonction quadratique. L'image se déformera en temps réel comme une animation, et les données de coordonnées seront mises à jour de manière synchrone, révélant de manière intuitive l'impact des changements de paramètres sur l'image, et une meilleure compréhension de la connexion entre les concepts mathématiques.
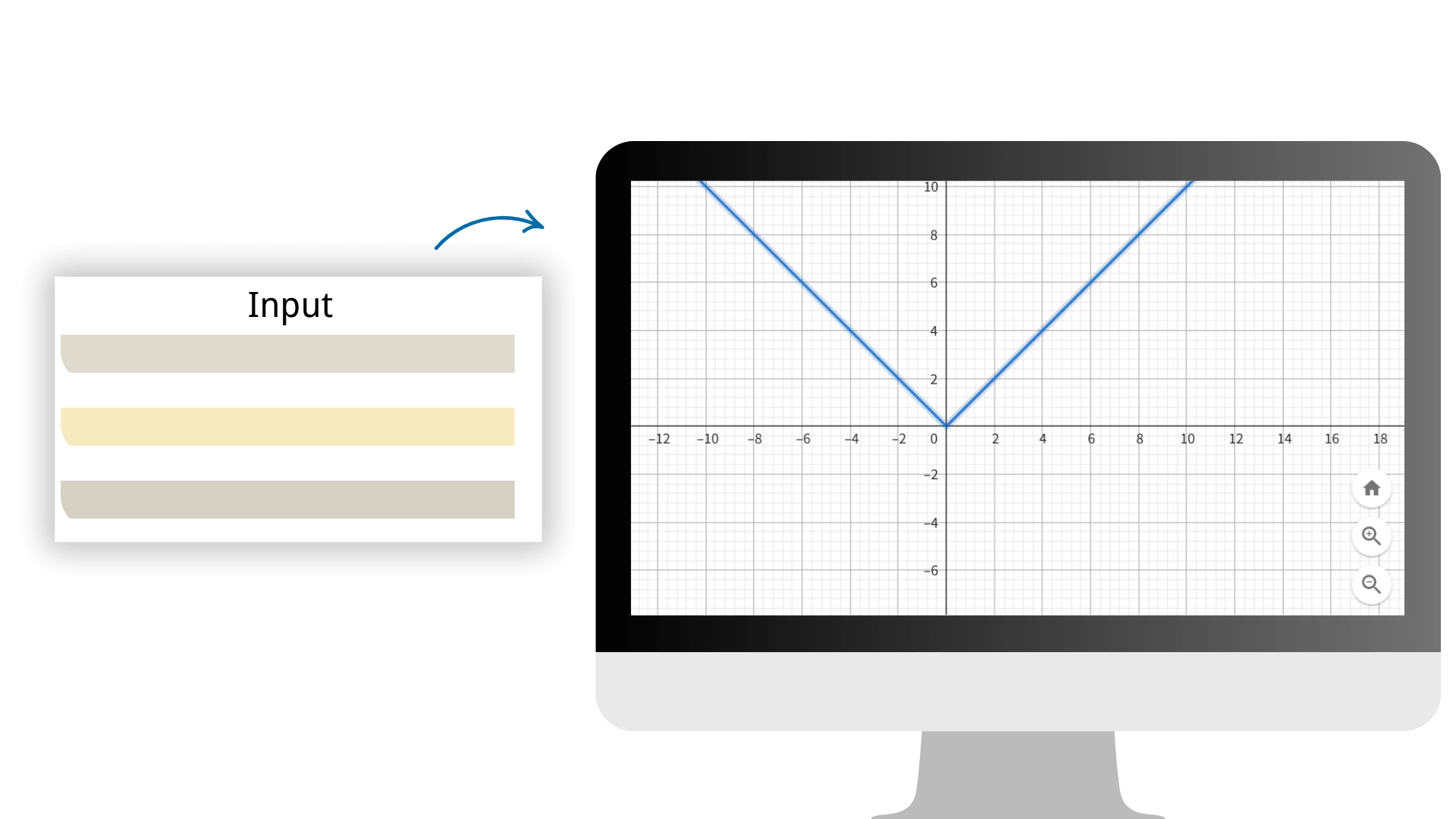
En adoptant des algorithmes de calcul avancés, nous nous assurons que chaque résultat de calcul a une précision extrêmement élevée, fournissant un support de données fiable pour votre travail mathématique. Il suffit d'entrer le tableau sur notre calculatrice d'image pour générer diverses images en un clic.
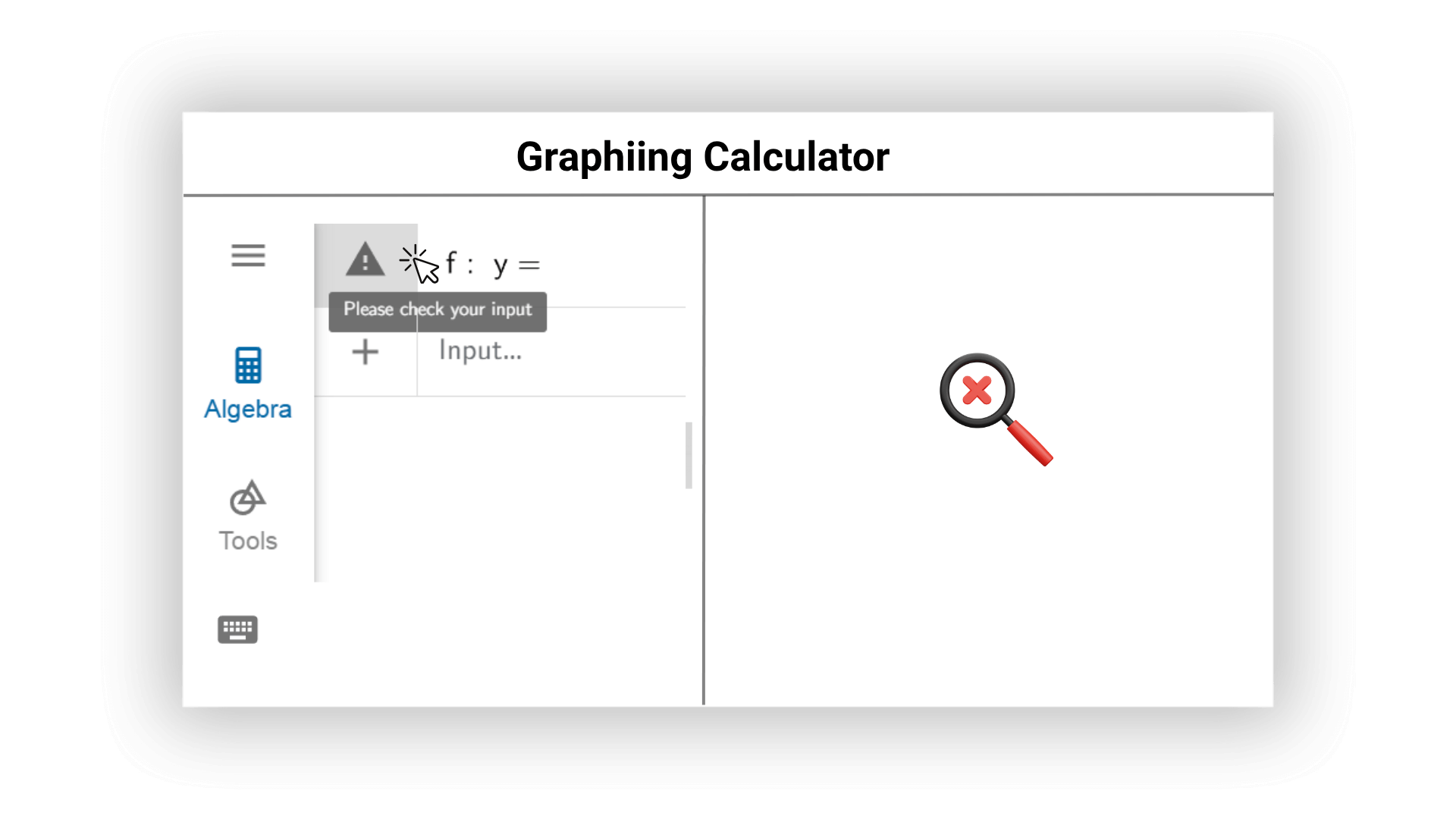
Notre calculatrice graphique AI peut vérifier en temps réel les erreurs possibles dans les expressions mathématiques en ligne et donner proactivement des suggestions de modification. L'IA peut rappeler aux utilisateurs les problèmes grammaticaux et les entrées non raisonnables pour garantir des résultats de calcul précis et une efficacité de calcul élevée, et éviter les erreurs dans les images et les résultats.
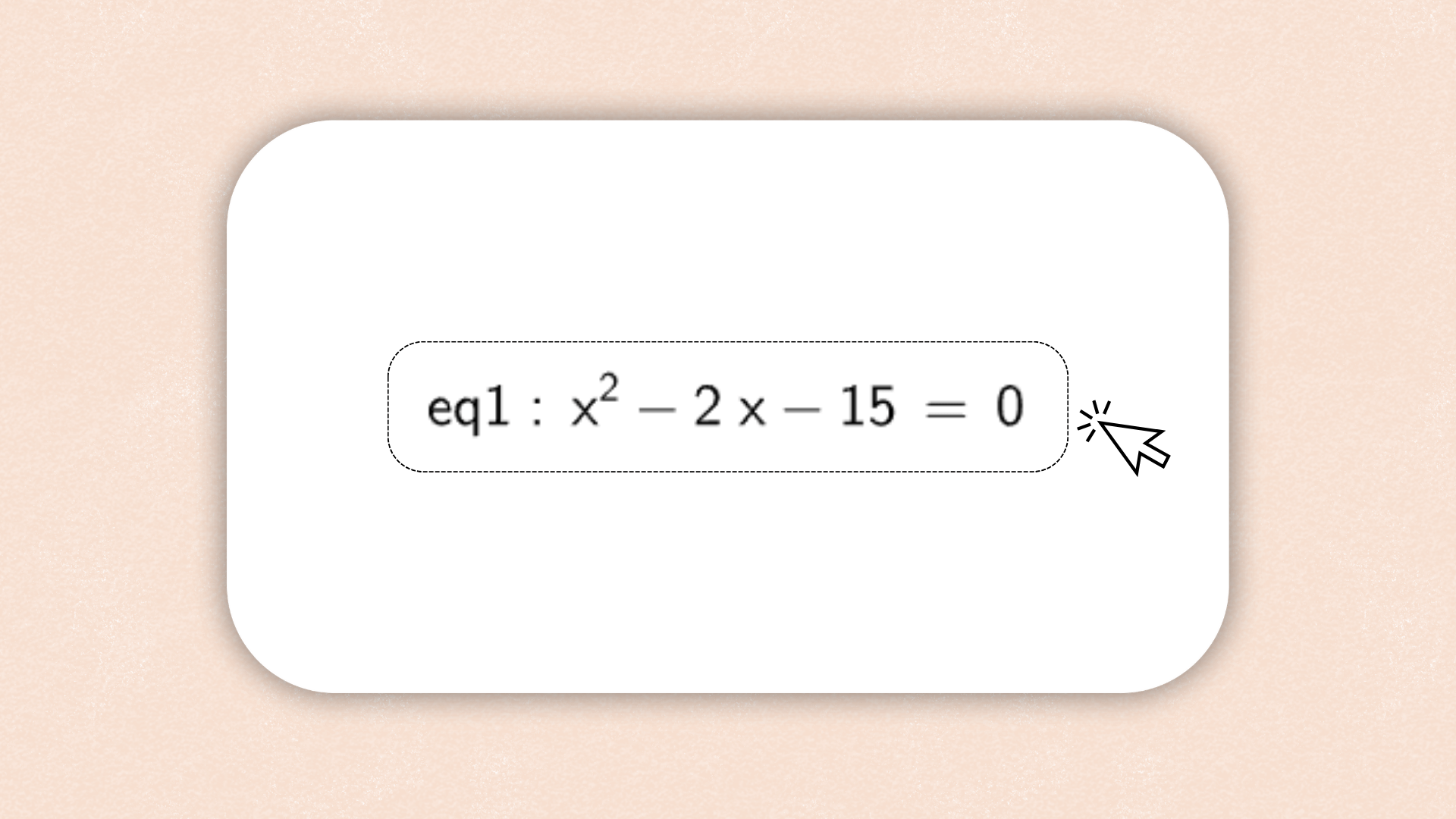
1. ![]() Entrez
Entrez y = m x + b dans la barre d'entrée et
appuyez sur la touche Entrée.
Astuce : La
Calculatrice Graphique créera automatiquement des curseurs
pour les paramètres m et b lors de la validation. Pour
afficher les curseurs dans la vue graphique, sélectionnez le
bouton de visibilité désactivé dans la vue algébrique à
gauche des variables.
2. ![]() Créez le point d'intersection A entre la droite et l'axe
des ordonnées.
Créez le point d'intersection A entre la droite et l'axe
des ordonnées.
Astuce : Vous pouvez utiliser
l'outil Intersection dans la boîte à outils pour les points
en sélectionnant les deux objets, ou utiliser la commande
Intersect(f, yAxis).
3. ![]() Créez un point B à l'origine en utilisant l'outil
Intersection et en sélectionnant les deux axes.
Créez un point B à l'origine en utilisant l'outil
Intersection et en sélectionnant les deux axes.
4. ![]() Sélectionnez l'outil Segment dans la boîte à outils pour
les droites et créez un segment entre les points A et B en
sélectionnant les deux points.
Sélectionnez l'outil Segment dans la boîte à outils pour
les droites et créez un segment entre les points A et B en
sélectionnant les deux points.
Astuce : Vous
pouvez aussi utiliser la commande Segment(A, B).
5. ![]() Masquez les points A et B en cliquant sur les boutons de
visibilité activés à gauche de leurs coordonnées dans la vue
algébrique.
Masquez les points A et B en cliquant sur les boutons de
visibilité activés à gauche de leurs coordonnées dans la vue
algébrique.
6. ![]() Utilisez l'outil Pente dans la boîte à outils Mesure pour
créer la pente (triangle) de la droite en cliquant sur la
droite.
Utilisez l'outil Pente dans la boîte à outils Mesure pour
créer la pente (triangle) de la droite en cliquant sur la
droite.
7. ![]() Améliorez l'apparence de votre construction à l'aide de la
barre de style (par exemple, augmentez l'épaisseur du
segment pour le rendre visible au-dessus de l'axe des
ordonnées).
Améliorez l'apparence de votre construction à l'aide de la
barre de style (par exemple, augmentez l'épaisseur du
segment pour le rendre visible au-dessus de l'axe des
ordonnées).
1. ![]() Tapez f(x) = x^2 dans la barre d'entrée et appuyez
sur Entrée.
Tapez f(x) = x^2 dans la barre d'entrée et appuyez
sur Entrée.
Quelle forme a le graphe de la fonction
?
2. ![]() Utilisez l'outil Déplacer et sélectionnez la fonction.
Cliquez sur la barre de style et choisissez de déverrouiller
la fonction. Vous pouvez maintenant faire glisser la
fonction dans la vue graphique et observer comment
l'équation dans la vue algébrique s'adapte à vos
modifications.
Utilisez l'outil Déplacer et sélectionnez la fonction.
Cliquez sur la barre de style et choisissez de déverrouiller
la fonction. Vous pouvez maintenant faire glisser la
fonction dans la vue graphique et observer comment
l'équation dans la vue algébrique s'adapte à vos
modifications.
3. ![]() Modifiez le graphe de la fonction pour que l'équation
corresponde à :
Modifiez le graphe de la fonction pour que l'équation
corresponde à :
f(x) = (x + 2)²
f(x) = x² - 3
et
f(x) = (x - 4)² + 2.
4. ![]() Sélectionnez l'équation du polynôme. Utilisez le clavier
pour changer l'équation en f(x) = 3 x^2.
Sélectionnez l'équation du polynôme. Utilisez le clavier
pour changer l'équation en f(x) = 3 x^2.
Comment
le graphe de la fonction change-t-il ?
5. ![]() Répétez la modification de l'équation en saisissant
différentes valeurs pour le paramètre (par exemple 0,5, -2,
-0,8, 3).
Répétez la modification de l'équation en saisissant
différentes valeurs pour le paramètre (par exemple 0,5, -2,
-0,8, 3).
1. ![]() Entrez f(x) = a*x³ + b*x² + c*x + d dans la barre
d'entrée et appuyez sur Entrée.
Entrez f(x) = a*x³ + b*x² + c*x + d dans la barre
d'entrée et appuyez sur Entrée.
Astuce : La Calculatrice Graphique créera
automatiquement des curseurs pour les paramètres a, b, c
et d.
2. ![]() Affichez les curseurs dans la vue graphique en
sélectionnant les boutons de visibilité désactivés à gauche
des entrées correspondantes dans la vue algébrique.
Affichez les curseurs dans la vue graphique en
sélectionnant les boutons de visibilité désactivés à gauche
des entrées correspondantes dans la vue algébrique.
3. ![]() Utilisez les curseurs dans la vue graphique pour modifier
les valeurs des paramètres avec l'outil Déplacer à
a = 0,2, b = -1,2, c = 0,6, d = 2.
Utilisez les curseurs dans la vue graphique pour modifier
les valeurs des paramètres avec l'outil Déplacer à
a = 0,2, b = -1,2, c = 0,6, d = 2.
4. ![]() Entrez R = Root(f) dans la barre d'entrée pour
afficher les racines du polynôme. Les racines seront
automatiquement nommées R1, R2 et R3.
Entrez R = Root(f) dans la barre d'entrée pour
afficher les racines du polynôme. Les racines seront
automatiquement nommées R1, R2 et R3.
5. ![]() Entrez E = Extremum(f) pour afficher les extrema
locaux du polynôme.
Entrez E = Extremum(f) pour afficher les extrema
locaux du polynôme.
6. ![]() Utilisez l'outil Tangente pour créer les tangentes au
polynôme passant par les extrema E1 et E2.
Utilisez l'outil Tangente pour créer les tangentes au
polynôme passant par les extrema E1 et E2.
Astuce : Ouvrez la boîte à outils Lignes
spéciales et sélectionnez l'outil Tangente. Sélectionnez
successivement le point E1 puis le polynôme pour créer la
tangente. Répétez pour le point E2.
7. ![]() Modifiez systématiquement les valeurs des curseurs à l'aide
de l'outil Déplacer pour explorer comment les paramètres
influencent le polynôme.
Modifiez systématiquement les valeurs des curseurs à l'aide
de l'outil Déplacer pour explorer comment les paramètres
influencent le polynôme.
1. ![]() Entrez l'équation linéaire
line_1: y = m_1 x + b_1 dans la barre d'entrée.
Entrez l'équation linéaire
line_1: y = m_1 x + b_1 dans la barre d'entrée.
Astuce : L'entrée line_1 vous donne la droite
1.
2. ![]() La Calculatrice Graphique créera automatiquement des
curseurs pour les variables m_1 et b_1 lors de
la validation.
La Calculatrice Graphique créera automatiquement des
curseurs pour les variables m_1 et b_1 lors de
la validation.
3. ![]() Affichez les curseurs dans la vue graphique en cliquant sur
les boutons de visibilité désactivés à côté de leur entrée
dans la vue algébrique.
Affichez les curseurs dans la vue graphique en cliquant sur
les boutons de visibilité désactivés à côté de leur entrée
dans la vue algébrique.
4. ![]() Répétez les étapes 1 à 3 pour l'équation de
line_2: y = m_2 x + b_2.
Répétez les étapes 1 à 3 pour l'équation de
line_2: y = m_2 x + b_2.
5. ![]() Utilisez la barre de style pour changer la couleur des deux
droites et de leurs curseurs.
Utilisez la barre de style pour changer la couleur des deux
droites et de leurs curseurs.
6. ![]() Utilisez l'outil Texte et créez un texte dynamique en
saisissant Ligne 1 : dans la boîte de dialogue qui
apparaît et en sélectionnant line_1 dans la liste des
objets de l'onglet Objets de la section Avancé.
Utilisez l'outil Texte et créez un texte dynamique en
saisissant Ligne 1 : dans la boîte de dialogue qui
apparaît et en sélectionnant line_1 dans la liste des
objets de l'onglet Objets de la section Avancé.
7. ![]() Créez un texte dynamique avec la partie statique
Ligne 2 : et sélectionnez line_2 dans la liste
des objets de l'onglet Objets de la section Avancé.
Créez un texte dynamique avec la partie statique
Ligne 2 : et sélectionnez line_2 dans la liste
des objets de l'onglet Objets de la section Avancé.
8. ![]() Utilisez la barre de style pour faire correspondre la
couleur des textes à celle de leurs droites
respectives.
Utilisez la barre de style pour faire correspondre la
couleur des textes à celle de leurs droites
respectives.
9. ![]() Construisez le point d'intersection A des deux
droites line_1 et line_2 en utilisant soit
l'outil Intersection, soit en saisissant la commande
Intersect(line_1, line_2) dans la barre
d'entrée.
Construisez le point d'intersection A des deux
droites line_1 et line_2 en utilisant soit
l'outil Intersection, soit en saisissant la commande
Intersect(line_1, line_2) dans la barre
d'entrée.
10. ![]() Entrez xcoordinate = x(A) dans la barre d'entrée.
Entrez xcoordinate = x(A) dans la barre d'entrée.
Astuce : x(A) vous donne l'abscisse du point
d'intersection A.
11. ![]() Définissez aussi ycoordinate = y(A).
Définissez aussi ycoordinate = y(A).
Astuce : y(A) vous donne l'ordonnée du point
d'intersection A.
12. ![]() Créez un texte dynamique avec la partie statique
Solution : x = et sélectionnez
xcoordinate dans la liste des objets de l'onglet
Objets.
Créez un texte dynamique avec la partie statique
Solution : x = et sélectionnez
xcoordinate dans la liste des objets de l'onglet
Objets.
13. ![]() Créez un texte dynamique avec la partie statique
y = et sélectionnez ycoordinate dans la liste
des objets de l'onglet Objets.
Créez un texte dynamique avec la partie statique
y = et sélectionnez ycoordinate dans la liste
des objets de l'onglet Objets.
14. ![]() Fixez les textes pour qu'ils ne puissent pas être déplacés
accidentellement en les sélectionnant puis en ouvrant la
barre de style.
Fixez les textes pour qu'ils ne puissent pas être déplacés
accidentellement en les sélectionnant puis en ouvrant la
barre de style.
1. ![]() Entrez le polynôme f(x) = x^2/2 + 1 dans la barre
d'entrée.
Entrez le polynôme f(x) = x^2/2 + 1 dans la barre
d'entrée.
2. ![]() Créez un nouveau point A sur la fonction
f.
Créez un nouveau point A sur la fonction
f.
Astuce : Le point A ne peut être déplacé que le
long de la fonction.
3. ![]() Créez la tangente g à la fonction f passant
par le point A.
Créez la tangente g à la fonction f passant
par le point A.
4. ![]() Créez la pente de la tangente g en utilisant
m = Slope(g).
Créez la pente de la tangente g en utilisant
m = Slope(g).
5. ![]() Définissez le point S = (x(A), m).
Définissez le point S = (x(A), m).
Astuce : x(A) vous donne l'abscisse du point
A.
6. ![]() Reliez les points A et S à l'aide d'un
segment.
Reliez les points A et S à l'aide d'un
segment.
7. ![]() Activez la trace du point S et déplacez le point
A.
Activez la trace du point S et déplacez le point
A.
Astuce : Faites un clic droit sur le point S
(MacOS : Ctrl-clic, tablette : appui long) et sélectionnez
Afficher la trace.
1. ![]() Entrez la fonction f(x) = sin(x) dans la barre
d'entrée.
Entrez la fonction f(x) = sin(x) dans la barre
d'entrée.
2. ![]() Faites un clic droit sur la vue graphique et sélectionnez
Graphiques... . Sélectionnez l'onglet xAxe et changez
l'unité en
Faites un clic droit sur la vue graphique et sélectionnez
Graphiques... . Sélectionnez l'onglet xAxe et changez
l'unité en π.
3. ![]() Créez un nouveau point A sur la fonction
f.
Créez un nouveau point A sur la fonction
f.
Astuce : Le point A ne peut être déplacé que le
long de la fonction.
4. ![]() Créez la tangente g à la fonction f passant
par le point A.
Créez la tangente g à la fonction f passant
par le point A.
5. ![]() Créez la pente de la tangente g à l'aide de l'outil
Pente.
Créez la pente de la tangente g à l'aide de l'outil
Pente.
6. ![]() Définissez le point S = (x(A), m).
Définissez le point S = (x(A), m).
Astuce : x(A) vous donne l'abscisse du point
A.
7. ![]() Reliez les points A et S à l'aide d'un
segment.
Reliez les points A et S à l'aide d'un
segment.
8. ![]() Activez la trace du point S et déplacez le point
A.
Activez la trace du point S et déplacez le point
A.
Astuce : Faites un clic droit sur le point S
(MacOS : Ctrl-clic, tablette : appui long) et sélectionnez
Afficher la trace.
9. ![]() Faites un clic droit (MacOS : Ctrl-clic, tablette : appui
long) sur le point A et choisissez
Animation dans le menu contextuel.
Faites un clic droit (MacOS : Ctrl-clic, tablette : appui
long) sur le point A et choisissez
Animation dans le menu contextuel.
Astuce : Un bouton Animation apparaît en bas à
gauche de la vue graphique. Il vous permet de mettre en
pause ou de continuer l'animation.
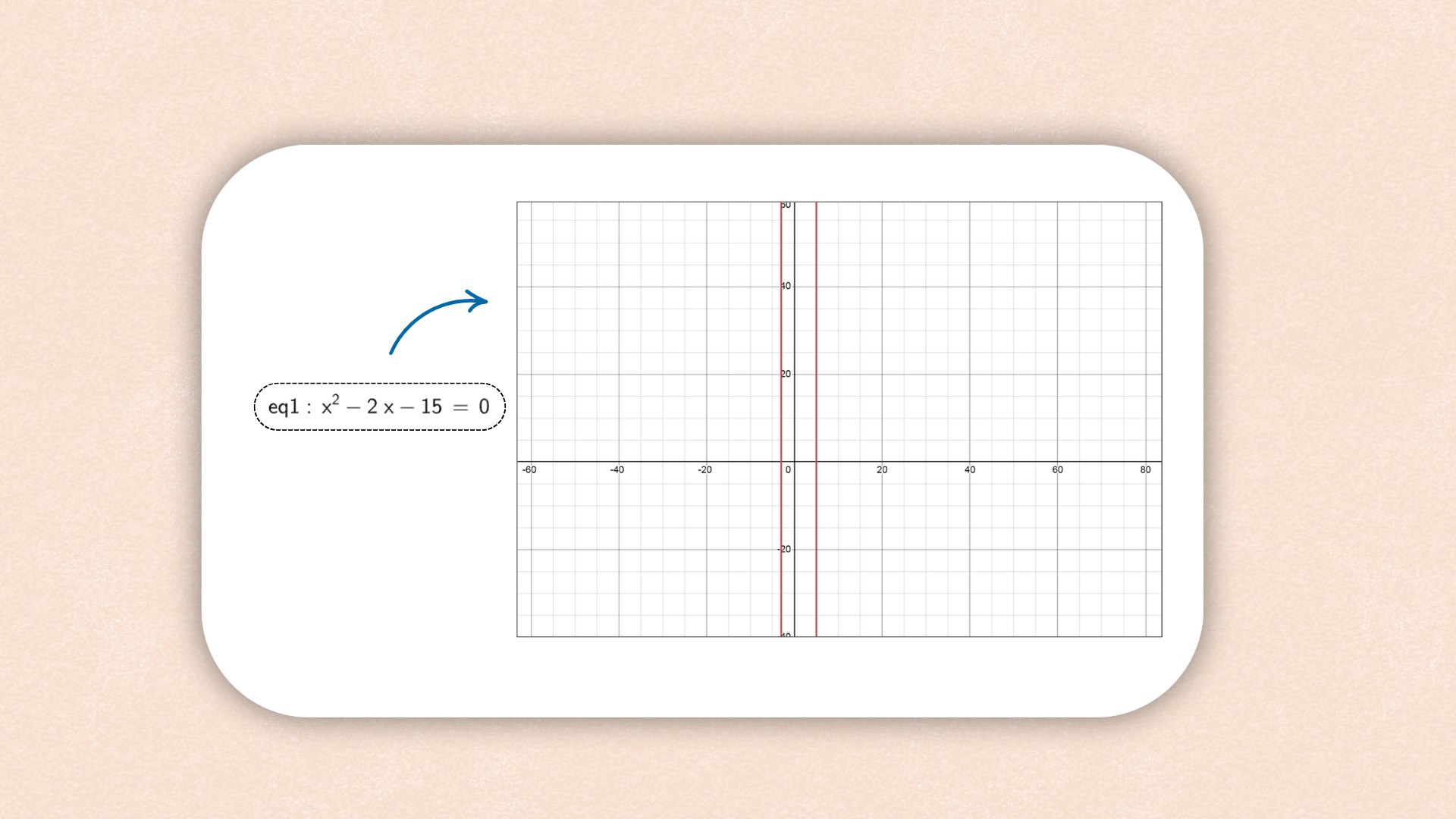
1. ![]() Entrez a x + b y ≤ c dans la barre d'entrée et
appuyez sur Entrée.
Entrez a x + b y ≤ c dans la barre d'entrée et
appuyez sur Entrée.
Astuce : Vous pouvez
utiliser le clavier virtuel pour entrer le symbole ≤. La
Calculatrice Graphique créera automatiquement des curseurs
pour les paramètres a, b et c.
2. ![]() Utilisez l'outil Déplacer pour ajuster les valeurs des
curseurs afin que a = 1, b = 1 et c = 3.
Utilisez l'outil Déplacer pour ajuster les valeurs des
curseurs afin que a = 1, b = 1 et c = 3.
3. ![]() Changez l'incrément des curseurs à 1.
Changez l'incrément des curseurs à 1.
Astuce :
Sélectionnez le nombre a et ouvrez la barre de style de la
vue graphique.
Ouvrez les paramètres du nombre a et sélectionnez l'onglet
Curseur.
Réglez l'incrément à 1 et répétez pour les nombres b et
c.
4. ![]() Faites glisser l'arrière-plan de la vue graphique pour
déplacer l'origine au centre.
Faites glisser l'arrière-plan de la vue graphique pour
déplacer l'origine au centre.
5. ![]() Dézoomez pour rendre une plus grande partie du système de
coordonnées visible à l'écran.
Dézoomez pour rendre une plus grande partie du système de
coordonnées visible à l'écran.
6. ![]() Réglez la distance entre les marques sur les axes à 1.
Réglez la distance entre les marques sur les axes à 1.
Astuce :
Assurez-vous qu'aucun objet n'est sélectionné avant d'ouvrir
la barre de style de la vue graphique.
Ouvrez les paramètres des axes.
Sélectionnez l'onglet xAxe et réglez la distance à 1.
Répétez pour l'onglet yAxe.
1. ![]() Entrez
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) dans
la barre d'entrée et appuyez sur Entrée.
Entrez
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) dans
la barre d'entrée et appuyez sur Entrée.
2. ![]() Créez un curseur s pour un nombre avec un intervalle
de 1 à 10 et un incrément de 1.
Créez un curseur s pour un nombre avec un intervalle
de 1 à 10 et un incrément de 1.
3. ![]() Entrez Sequence((i, i), i, 0, s) dans la barre
d'entrée et appuyez sur Entrée.
Entrez Sequence((i, i), i, 0, s) dans la barre
d'entrée et appuyez sur Entrée.
4. ![]() Déplacez le curseur s pour vérifier la
construction.
Déplacez le curseur s pour vérifier la
construction.
1. ![]() Ouvrez les paramètres de la vue graphique à l'aide de la
barre de style.
Ouvrez les paramètres de la vue graphique à l'aide de la
barre de style.
2. ![]() Dans l'onglet xAxe, réglez la distance des graduations à 1
en cochant la case Distance et en saisissant 1 dans le champ
de texte.
Dans l'onglet xAxe, réglez la distance des graduations à 1
en cochant la case Distance et en saisissant 1 dans le champ
de texte.
3. ![]() Dans l'onglet Basique, réglez le minimum de l'axe x à -11
et le maximum à 11.
Dans l'onglet Basique, réglez le minimum de l'axe x à -11
et le maximum à 11.
4. ![]() Dans l'onglet yAxe, décochez Afficher l'axe y et fermez les
paramètres.
Dans l'onglet yAxe, décochez Afficher l'axe y et fermez les
paramètres.
5. ![]() Créez deux curseurs a et b, tous deux avec un
intervalle de -5 à 5 et un incrément de 1.
Créez deux curseurs a et b, tous deux avec un
intervalle de -5 à 5 et un incrément de 1.
6. ![]() Affichez la valeur des curseurs au lieu de leur nom à
l'aide de la barre de style.
Affichez la valeur des curseurs au lieu de leur nom à
l'aide de la barre de style.
7. ![]() Créez les points A = (0, 1) et
B = A + (a, 0).
Créez les points A = (0, 1) et
B = A + (a, 0).
Astuce : La distance du point B au point A est
déterminée par le curseur a.
8. ![]() Créez un vecteur u = Vector(A, B) de longueur
a.
Créez un vecteur u = Vector(A, B) de longueur
a.
9. ![]() Créez les points C = B + (0, 1) et
D = C + (b, 0).
Créez les points C = B + (0, 1) et
D = C + (b, 0).
10. ![]() Créez le vecteur v = Vector(C, D) de longueur
b.
Créez le vecteur v = Vector(C, D) de longueur
b.
11. ![]() Créez le point R = (x(D), 0).
Créez le point R = (x(D), 0).
Astuce : L'entrée x(D) vous donne l'abscisse du
point D. Ainsi, le point R montre le résultat de
l'addition sur la droite numérique.
12. ![]() Créez le point Z = (0, 0).
Créez le point Z = (0, 0).
13. ![]() Créez trois segments c = Segment(Z, A),
d = Segment(B, C) et e = Segment(D, R).
Créez trois segments c = Segment(Z, A),
d = Segment(B, C) et e = Segment(D, R).
14. ![]() Utilisez la barre de style pour améliorer votre
construction (par exemple, faire correspondre la couleur des
curseurs et des vecteurs, changer le style de ligne, fixer
les curseurs, masquer les étiquettes et les points).
Utilisez la barre de style pour améliorer votre
construction (par exemple, faire correspondre la couleur des
curseurs et des vecteurs, changer le style de ligne, fixer
les curseurs, masquer les étiquettes et les points).
1. ![]() Créez un curseur horizontal nommé Colonnes pour un
nombre avec un intervalle de 1 à 10, un incrément de 1 et
une largeur de 300.
Créez un curseur horizontal nommé Colonnes pour un
nombre avec un intervalle de 1 à 10, un incrément de 1 et
une largeur de 300.
Astuce : Vous pouvez
modifier la largeur du curseur dans l'onglet Paramètres sous
Curseur.
2. ![]() Créez un nouveau point A.
Créez un nouveau point A.
3. ![]() Construisez le segment f de longueur
Colonnes à partir du point A.
Construisez le segment f de longueur
Colonnes à partir du point A.
4. ![]() Déplacez le curseur Colonnes pour observer le segment de la
longueur spécifiée.
Déplacez le curseur Colonnes pour observer le segment de la
longueur spécifiée.
5. ![]() Construisez une droite perpendiculaire g au segment
f passant par le point A.
Construisez une droite perpendiculaire g au segment
f passant par le point A.
6. ![]() Construisez une droite perpendiculaire h au segment
f passant par le point B.
Construisez une droite perpendiculaire h au segment
f passant par le point B.
7. ![]() Créez un curseur vertical nommé Lignes pour un
nombre avec un intervalle de 1 à 10, un incrément de 1 et
une largeur de 300.
Créez un curseur vertical nommé Lignes pour un
nombre avec un intervalle de 1 à 10, un incrément de 1 et
une largeur de 300.
Astuce : Vous pouvez
choisir l'orientation du curseur dans la boîte de dialogue
Curseur sous l'onglet Curseur.
8. ![]() Créez un cercle c de centre A et de rayon
Lignes.
Créez un cercle c de centre A et de rayon
Lignes.
9. ![]() Déplacez le curseur Lignes pour observer le cercle de rayon
spécifié.
Déplacez le curseur Lignes pour observer le cercle de rayon
spécifié.
10. ![]() Intersequez le cercle c avec la droite g pour obtenir le
point d'intersection C.
Intersequez le cercle c avec la droite g pour obtenir le
point d'intersection C.
Astuce : Lors
de la sélection de l'outil Intersection, cliquez sur le
point d'intersection au-dessus du point A pour ne créer que
ce point.
11. ![]() Créez une droite parallèle i au segment f passant
par le point d'intersection C.
Créez une droite parallèle i au segment f passant
par le point d'intersection C.
12. ![]() Intersequez les droites i et h pour obtenir le point
d'intersection D.
Intersequez les droites i et h pour obtenir le point
d'intersection D.
13. ![]() Construisez un polygone ABDC.
Construisez un polygone ABDC.
14. ![]() Masquez toutes les droites, le cercle c et le segment
f.
Masquez toutes les droites, le cercle c et le segment
f.
15. ![]() Masquez les étiquettes des segments à l'aide de la barre de
style.
Masquez les étiquettes des segments à l'aide de la barre de
style.
16. ![]() Réglez les curseurs Colonnes et Lignes sur la valeur
10.
Réglez les curseurs Colonnes et Lignes sur la valeur
10.
17. ![]() Créez une liste de segments verticaux en utilisant :
Créez une liste de segments verticaux en utilisant :
Sequence(Segment(A + i*(1, 0), C + i*(1, 0)), i, 1,
Colonnes)
Remarque : A + i*(1, 0) spécifie une série de points à
partir du point A espacés de 1.
C + i*(1, 0) spécifie
une série de points à partir du point C espacés de 1.
Segment(A
+ i*(1, 0), C + i*(1, 0)) crée une liste de segments entre
ces paires de points. Remarque : les extrémités des segments
ne sont pas affichées dans la vue graphique.
Le curseur
Colonnes détermine le nombre de segments créés.
18. ![]() Créez une liste de segments horizontaux.
Créez une liste de segments horizontaux.Sequence(Segment(A + i*(0, 1), B + i*(0, 1)), i, 1,
Lignes)
19. ![]() Déplacez les curseurs Colonnes et Lignes pour observer la
construction.
Déplacez les curseurs Colonnes et Lignes pour observer la
construction.
20. ![]() Insérez du texte statique et dynamique pour énoncer le
problème de multiplication en utilisant les valeurs de
Colonnes et Lignes comme facteurs :
Insérez du texte statique et dynamique pour énoncer le
problème de multiplication en utilisant les valeurs de
Colonnes et Lignes comme facteurs :texte1 : Colonnestexte2 : *texte3 : Lignestexte4 : =
21. ![]() Calculez le résultat de la multiplication :
Calculez le résultat de la multiplication :
résultat = Colonnes * Lignes
22. ![]() Insérez le texte dynamique5 :
Insérez le texte dynamique5 : résultat
23. ![]() Masquez les points A, B, C et D.
Masquez les points A, B, C et D.
24. ![]() Améliorez votre construction à l'aide de la barre de
style.
Améliorez votre construction à l'aide de la barre de
style.
La calculatrice graphique AI est un assistant puissant pour les étudiants pour apprendre les mathématiques. Du collège à l'université, que ce soit pour les cours d'algèbre, de géométrie, de calcul ou de statistiques, elle peut aider les étudiants à mieux comprendre et à maîtriser les connaissances mathématiques, améliorant ainsi l'efficacité de l'apprentissage et les notes. Les enseignants peuvent l'utiliser pour conduire des démonstrations pédagogiques et créer des supports de cours vivants pour stimuler l'intérêt et l'enthousiasme des étudiants pour l'apprentissage.
Elle fournit aux chercheurs des outils mathématiques puissants pour faciliter le traitement des données, l'analyse expérimentale, la construction de modèles et la vérification théorique. Dans divers domaines scientifiques tels que la physique, la chimie, la biologie et l'ingénierie, les calculateurs graphiques peuvent être utilisés pour achever rapidement et avec précision des opérations mathématiques complexes et des analyses de données, aidant ainsi au développement fluide de la recherche scientifique.
Utilisez la calculatrice graphique pour dessiner des courbes d'offre et de demande, des modèles de croissance composée, etc., analyser l'intersection des fonctions de coût marginal et de revenu, et aider dans la prise de décision commerciale.
La calculatrice graphique bénéficie aux étudiants du primaire à l'université. Elle les aide à comprendre les concepts mathématiques et à cultiver des compétences de résolution de problèmes.

Les enseignants de mathématiques peuvent utiliser la calculatrice graphique pour créer des matériaux de cours et démontrer les concepts et les processus de résolution de problèmes, améliorant ainsi l'efficacité de l'enseignement et l'interaction.

Les chercheurs dans divers domaines comptent sur elle pour les calculs mathématiques complexes et l'analyse de données. La calculatrice graphique en ligne fournit des résultats précis qui accélèrent la recherche.

Dites adieu au dessin manuel fastidieux, générez des graphiques de visualisation de données professionnels avec un seul clic, tracez des graphiques de fonction en ligne, annotiez la moyenne et la variance en temps réel, ajustez dynamiquement les courbes de régression, et complétez efficacement l'intégration et l'analyse des données.

Les calculatrices graphiques aident les ingénieurs logiciels à visualiser les algorithmes de filtre et à optimiser les paramètres de rendu, garantissant une performance de fonction pixel parfaite.

Pour les designers architecturaux, les calculatrices graphiques sont des puissances paramétriques de conception, entrez les équations de courbe pour générer des graphiques de fonction/déplacement, validez visuellement la mécanique structurelle, et réduisez les cycles de conception.

Toutes les fonctions ne nécessitent pas d'inscription ou de paiement, et vous pouvez les utiliser tout le temps.
Maintenez une haute précision lors du calcul de problèmes avancés tels que les déterminants de matrices et les intégrales pour éviter les erreurs de recherche scientifique.
Le calcul est entièrement réalisé dans le navigateur, aucune donnée n'est téléchargée, et la page est effacée lorsqu'elle est fermée.
Aucun téléchargement ou installation nécessaire, les téléphones mobiles et les ordinateurs peuvent être utilisés immédiatement.
Concentrez-vous sur l'essence de l'apprentissage, sans pop-up, sans publicités, et améliorez votre concentration.
Que ce soit pour des applications académiques, de recherche scientifique, de bureau ou d'ingénierie, nous pouvons répondre à vos besoins de calcul graphique.
Vous n'avez pas besoin de vous inscrire ou de télécharger de logiciel. Il suffit d'entrer notre site web dans votre navigateur et de commencer à utiliser cet outil puissant de calculatrice graphique. Vous pouvez expérimenter sa commodité immédiatement.
Oui, notre calculatrice graphique AI est complètement gratuite. Malgré être gratuite, elle ne restreint pas les fonctionnalités essentielles. Vous pouvez utiliser pleinement ses fonctions de graphique, de calcul et d'analyse de données sans coût. Nous visons à offrir un outil mathématique pratique et efficace pour tout le monde.
Nous priorisons la sécurité et la confidentialité de vos données. Toutes vos calculs, graphiques et données d'entrée sont traités localement dans votre navigateur et ne sont jamais téléchargés ou stockés sur nos serveurs. Vous pouvez l'utiliser avec confiance, sachant que vos données sont en sécurité.
Pour entrer une fonction, il suffit de taper la formule dans la boîte d'entrée sur la page d'accueil. Par exemple, entrez "y=2x^2" ou "f(x)=sin(x)". La calculatrice traitera automatiquement votre entrée et affichera le graphique.
Oui, la Calculatrice Graphique AI peut gérer une variété de fonctions, allant des équations linéaires simples aux équations avancées comme les intégrales, les dérivées et les équations multivariables. Elle convient à la fois pour les besoins mathématiques de base et avancés, ce qui en fait un outil idéal pour les étudiants et les professionnels.
Oui, elle est entièrement accessible sur les appareils mobiles. Vous pouvez l'utiliser sur des smartphones ou des tablettes, et elle est optimisée pour toutes les tailles d'écran, garantissant une expérience fluide partout où vous êtes.