無料オンライン方程式計算機 | 分かりやすいステップ式でんたく
無料の方程式計算機。テキストや画像から一次方程式問題、二次方程式、連立方程式、線形方程式、多項式方程式、根号方程式、指数および対数方程式まで、幅広いタイプの方程式を解くことができます。方程式を入力するだけで、解、ステップ瞬時に取得可能です。

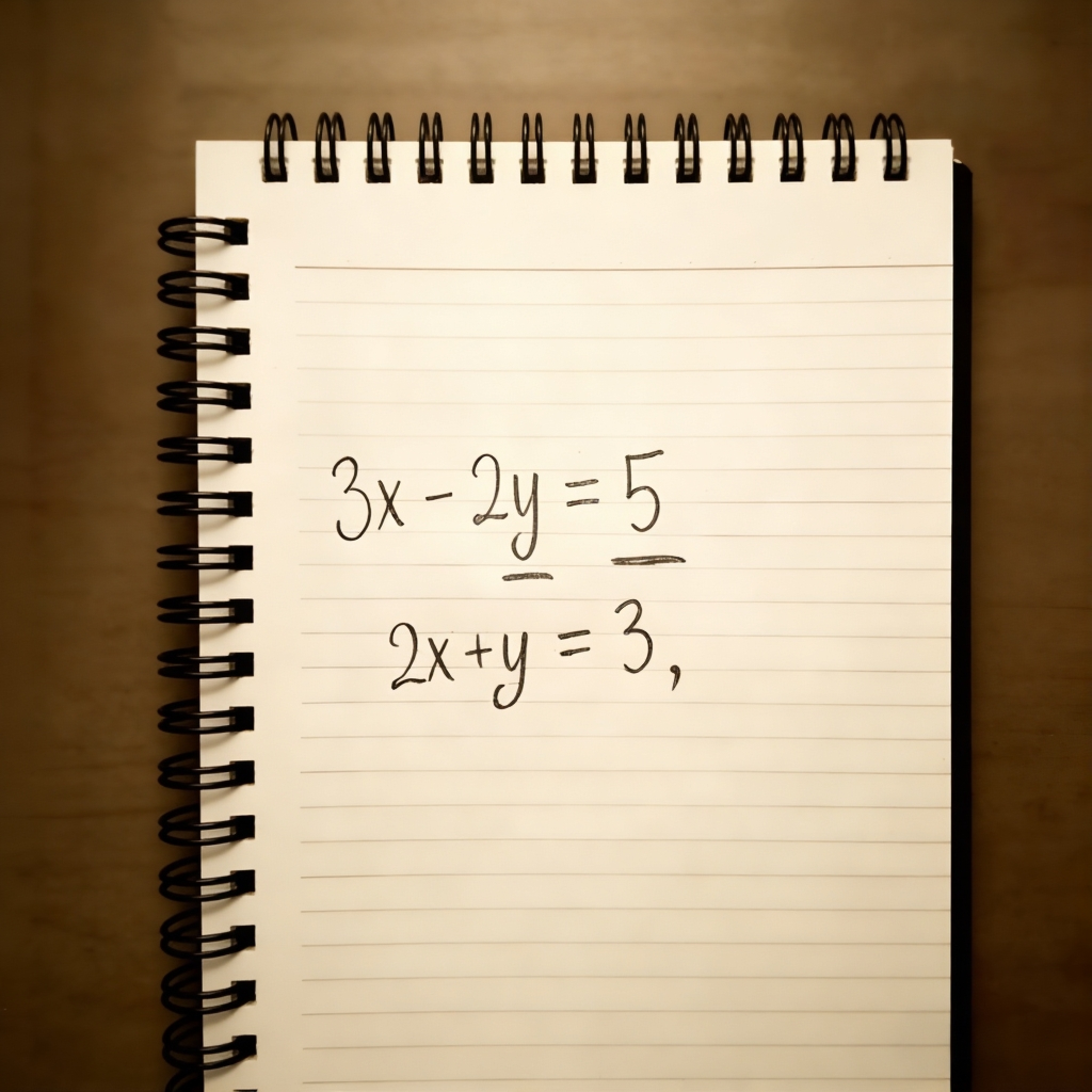

方程式とは何ですか?
方程式とは、未知数xを含む等式のことであり未知数を求めるために、既知の数との関係を式として表します。一般的な方程式の解き方には、一次方程式問題、2次方程式、三角関数方程式、対数方程式、三次方程式などがあります。
方程式は、数学だけでなく、物理、工学、経済学などさまざまな分野で広く使われており、現実世界の問題を理解し、解決するための重要なツールです。
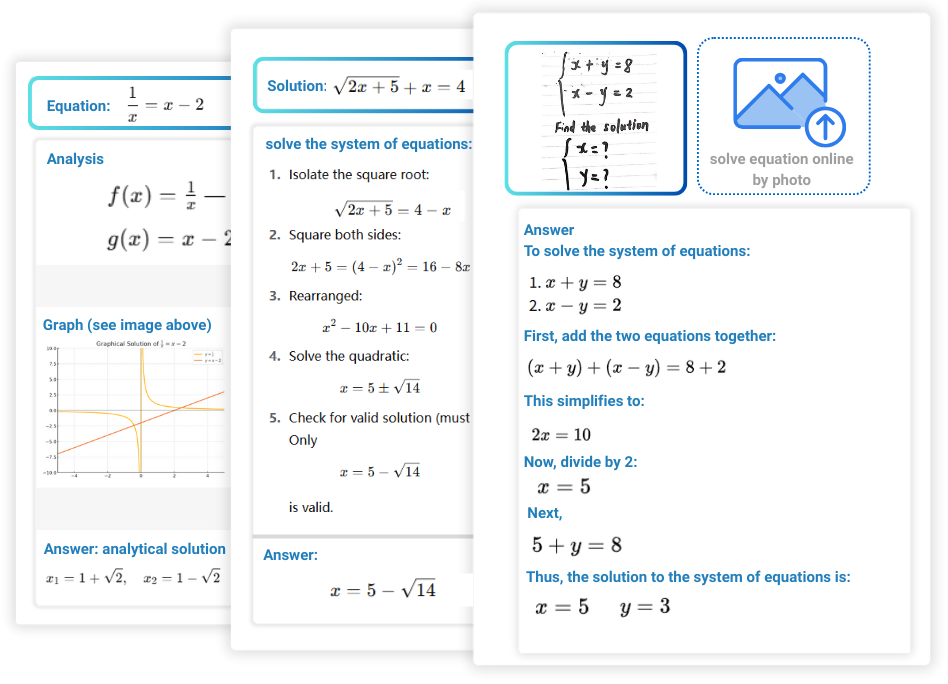
方程式計算機とは何ですか?
方程式計算機は、数学AIを活用した、数学の問題を迅速かつ正確に解決するための方程式計算サイトです。アルゴリズムによる解析を通じて、ユーザーが入力した方程式や方程式の画像をもとに、迅速かつ正確に解を導き出します。その解法は、ステップバイステップで詳しく表示されるため、理解しやすく学習にも役立ちます。
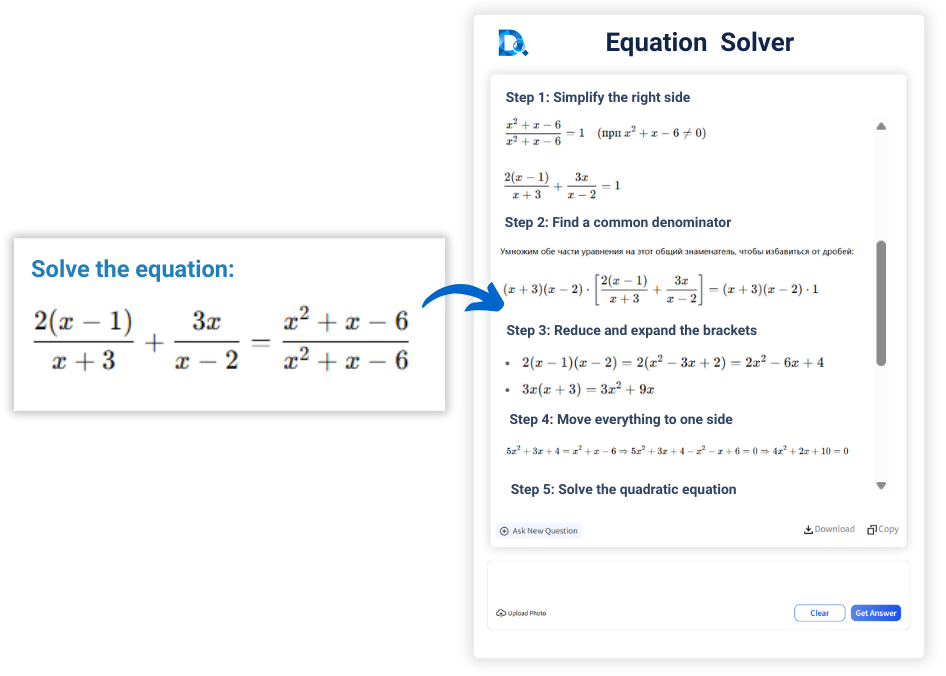
方程式の解き方は?
替わりに、オンラインの方程式計算機を使用すると、方程式の写真を簡単にアップロードしたり、直接入力したりするだけで、正確な答えをすばやく得ることができます。AI 数学方程式ソルバーは、代入法、加減法、2次方程式の解の公式など、人間の解法手順をシミュレートし、すべてのステップバイステップの解答を表示します。

Decopy AIの方程式計算機はどのように方程式を解くの?
Decopy
AIの方程式計算機は、代数、数値解析、アルゴリズム最適化を組み合わせた高度なAI数学エンジンによって動作しています。
ユーザーが数式を入力またはアップロードすると、システムは自動的に方程式の種類(一次方程式、2次方程式、三角関数、対数関数など)を判別し、それに応じて最適な解き方を選択します:
一次方程式や連立方程式の場合、ガウス消去法や行列計算により高速に解を求めます。
2次方程式には、判別式に基づいた2次方程式 解の公式を使ってステップ・バイ・ステップで解を導きます。
三角関数や対数方程式、三次方程式には、標準的な変形、因数分解、または数値近似法を適用します。
より複雑な非線形方程式系には、数値計算や高度なソルバーを使用します。
このオンライン方程式計算機は、最終的な答えだけでなく、段階的な解き方(数学問題の理解)も表示し、学習や理解をサポートします。また、電卓
無料アプリとして、シンプルで広告なしのインターフェースを提供します。

方程式計算機の特徴
写真や手動入力で、あらゆる数学問題をオンライン方程式計算機で、すばやく・正確に解くことができ、段階的な解析にも対応しています。
写真で方程式計算機
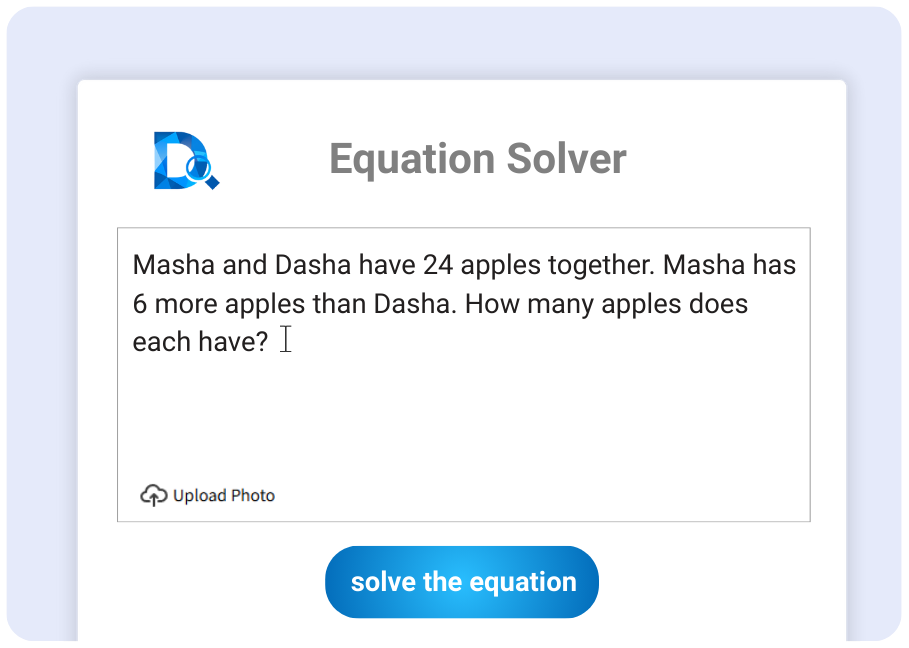
手動入力
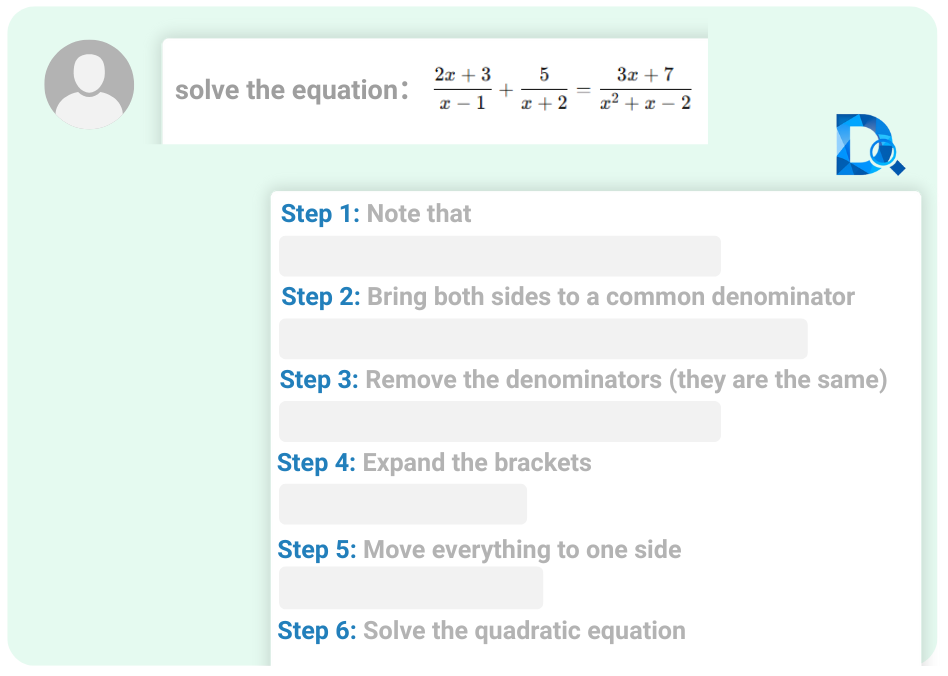
ステップ・バイ・ステップの解答

多種類の方程式計算機に対応
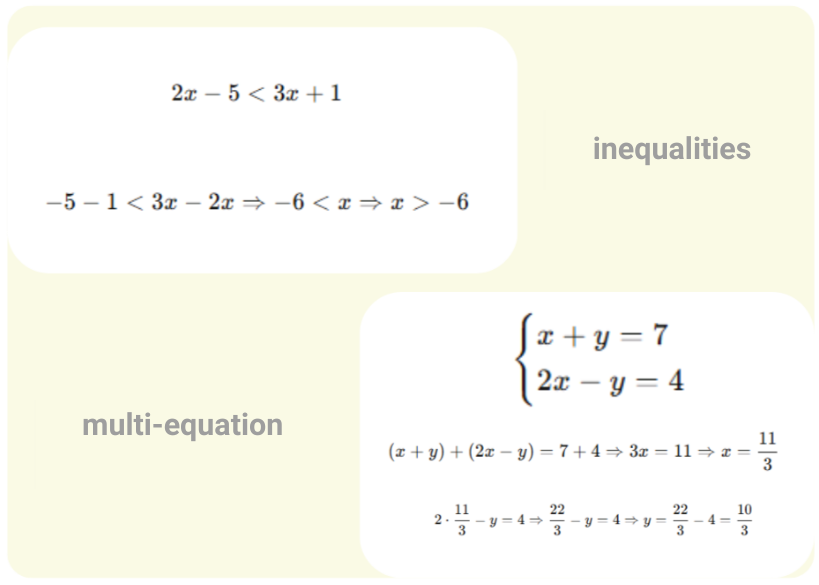
不等式と連立方程式の解法
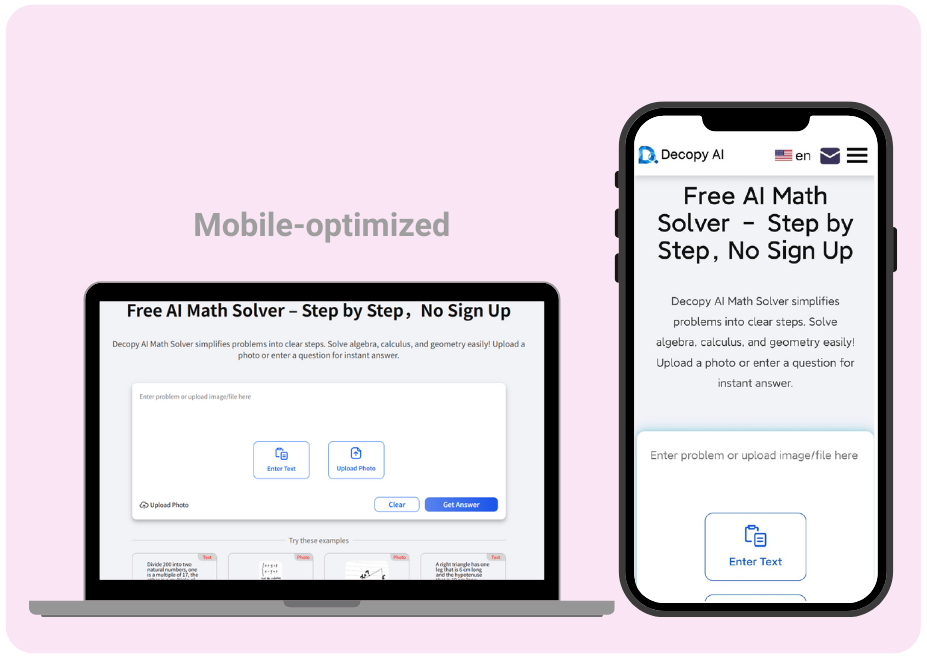
モバイル対応
いつでもどこでも使える方程式計算機
写真入力や手動入力に対応したモバイルフレンドリーなオンライン 方程式計算サイトで、**段階的に(ステップ・バイ・ステップ)**解き方をサポートします。

学生の課題

試験の復習

教室サポート

複雑な検証

指導の評価

セルフスタディ
方程式の種類と対応状況
この方程式計算機では、以下のような数学方程式に対応しています。どんなに複雑な問題でも、分かりやすいステップごとの解き方を提供します。
| 方程式の種類 | 一般形式 | 解の特徴 |
|---|---|---|
| 一次方程式 | ax + b = 0 | 一つの根、再配置と除算で解く |
| 二次方程式 | ax² + bx + c = 0 | 二次方程式の公式、最大二つの解 |
| 四次方程式 | x⁴ + bx² + c = 0 | 変数置換を使用して解く |
| 多項式方程式 | aₙxⁿ + ... + a₀ = 0 | 最大n個の実数または複素数の根 |
| 対数方程式 | log_b(f(x)) = g(x) | f(x) = b^g(x)として書き換えて解く |
| 指数方程式 | a^{f(x)} = b^{g(x)} | 両辺の対数変換 |
| 根方程式 | √f(x) = g(x) | 両辺を平方して、定義域を確認 |
| 絶対値方程式 | |f(x)| = g(x) | 二つの場合: f(x)=g(x)とf(x)=–g(x) |
| 三角関数方程式 | sin(x), cos(x), ... | 周期性と恒等式を使用 |
| 複素方程式 | f(z) = 0 | 複素平面内の解 |
| 行列方程式 | AX = B | 線形代数の方法、逆行列 |
| 有理方程式 | P(x)/Q(x) = 0 | 定義域を確認し、有理根を見つける |
| 床関数方程式 | ⌊f(x)⌋ = g(x) | 整数区間内で解く |
| 根に基づく構築 | f(x) = (x − r₁)... | 既知の根から多項式を構築 |
| 点に基づく構築 | f(x) through (x₁, y₁)... | 補間方法 |
| 数値方法 | f(x) = 0 | 近似根の探索(例: ニュートン法) |
| 微分方程式 | y', y'' = f(x) | 解法を通じて関数y(x)を見つける |
Decopy AI 方程式計算機の使い方
- 1
ウェブサイトにアクセスし、「方程式計算機」ページを開きます。
- 2
写真をアップロードするか、方程式を直接入力します。
- 3
「解き始める」ボタンをクリックすると、システムが自動で解析を開始します。
- 4
段階的な(ステップ・バイ・ステップの)解き方を表示したり、さらに質問することも可能です。
なぜ私たちの方程式計算機を使うべきか?
100% 完全無料
サインアップ不要、広告なし、そして一切の隠れた料金もありません。今すぐオンラインで方程式を解き始めましょう。
高精度で信頼できる
独自のインテリジェントアルゴリズムにより、方程式計算機はあらゆる種類の数学の方程式を正確に処理します。
シンプルで使いやすい
初心者でも簡単に使えるインターフェースで、誰でもすぐに数学の問題を解くことができます。
多言語対応
この方程式計算機は8カ国語に対応しており、国際的な試験や多言語環境でも安心して使用できます。
ダウンロード不要
アプリのインストールは必要ありません。ブラウザ上でそのまま利用可能です。
さまざまな方程式に対応
一次方程式、2次方程式、連立方程式、三角方程式など、幅広い数学問題に対応。学習や試験対策にも最適です。
お客様の声
よくある質問(FAQ)
数学の問題は種類によって適切な解法が異なります。以下は代表的な解き方です:
代入法:2つの変数を含む連立方程式の解き方としてよく使われます。
加減法(消去法):変数を消して一つの方程式に変形し、解を導き出す方法です。
平方完成/解の公式:2次方程式の解き方に有効です。特に係数が複雑なときに便利です。
グラフ・数値的手法:解析的に解けない高次方程式や複雑な構造を持つ方程式に適用されます。
方程式計算機:構造が複雑だったり、時間のかかる方程式を効率的に処理できるオンラインの電卓無料アプリです。さらに、ステップ・バイ・ステップの解説付きで、学習にも最適です。
平方完成とは、次のような形の2次方程式ax² + bx + c = 0を、以下のような平方の形に変形する手法です:
(x
+ d)² = e
これにより、視覚的にも解きやすくなります。特に、標準的な方法では扱いづらい係数を含む2次方程式の解の公式の代わりとして使うと効果的です。
方程式の解き方において最も重要なルールは、左右のバランスを保つことです。どんな操作(加減乗除)でも、一方の辺に施した操作は必ずもう一方にも同様に行う必要があります。そうしなければ、「=」という等式の基本的な原則が崩れてしまい、誤った答えに導かれる可能性があります。
1. 項を移動する:変数を片側に集め、定数を反対側に移動します。
2.
式を簡略化する:同類項をまとめて式をシンプルにします。
3. 解を求める:加減乗除を使って、x =
値の形にします。この際も左右同時に操作することがポイントです。
方程式を簡単化(簡略化)することは、基本的な手順のひとつです。具体的には:
1. かっこを外す
2.
同類項をまとめる(例:3x + 2x = 5x)
3. 計算の順序に従う (かっこ → べき乗 → 乗除 →
加減)これにより、数学問題をより分かりやすく、計算しやすい形に整えられます。
1. 両辺を簡略化:かっこの展開や同類項の整理を行う。
2. 変数を孤立させる:変数を含む項を片側に集める。
3. 変数の値を求める:逆演算(加減乗除の逆)を使って、係数を処理し、最終的な答えを求める。
Decopy AI 方程式計算機の使い方はとても簡単です。オンラインで数学の方程式を入力すると、Decopy AI の方程式計算機が自動で変数や構造を認識し、代数変換・数値計算などのAIアルゴリズムで方程式を即座に解きます。さらに、各ステップに対して詳細な解説付きで表示されるため、理解を深めたい方や、宿題の確認・複雑な例題の検証にもぴったりです。
📘 対応している数学関数の一覧
Decopy AIの方程式計算機で使用できる構文や記号についてご確認いただけます。
📂 対応している関数を表示
| 関数 | 説明 |
|---|---|
| abs(x) | xの絶対値 |
| arccos(x) | xの逆余弦 |
| arccosh(x) | 双曲線逆余弦 |
| arcsin(x) | xの逆正弦 |
| arcsinh(x) | 双曲線逆正弦 |
| arctg(x) | xの逆正接 |
| arctgh(x) | 双曲線逆正接 |
| asec(x) | xの逆余割 |
| asech(x) | 双曲線逆余割 |
| cbrt(x) | xの立方根 |
| ceiling(x) | 最も近い整数への切り上げ |
| chi(x) | 双曲線余弦積分 |
| cos(x) | xの余弦 |
| cosh(x) | 双曲線余弦 |
| cosec(x), csc(x) | xの余割 |
| ctg(x) | xの余接 |
| diracdelta(x) | ディラックのデルタ関数 |
| e | オイラーの数 ≈ 2.71828 |
| exp(x) | 指数関数 (e^x) |
| factorial(x), x! | xの階乗 |
| floor(x) | 最も近い整数への切り捨て |
| gamma(x) | ガンマ関数 |
| heaviside(x) | ヘヴィサイドの階段関数 |
| i | 虚数単位 (√-1) |
| lambertw(x) | ランベルトW関数 |
| ln(x), log(x) | 自然対数 |
| log(a,x) | 底aの対数 |
| oo | 無限大 |
| pi | 円周率 ≈ 3.14159 |
| sec(x) | xの正割 |
| sech(x) | 双曲線正割 |
| sign(x) | 数の符号 |
| sin(x) | xの正弦 |
| sinh(x) | 双曲線正弦 |
| sqrt(x) | 平方根 |
| sqr(x), x^2 | xの平方 |
| Si(x), Ci(x), Shi(x), Chi(x) | 積分三角関数と双曲線関数 |
| tg(x), tan(x) | 正接 |
| tgh(x) | 双曲線正接 |
| x + y, x - y | 加法、減法 |
| x * y, x / y | 乗法、除法 |
| x^n, pow(x,n) | 冪乗 |





