学生
グラフ計算機は、小学生から大学生までの学生に利益をもたらします。数学の概念を理解し、問題解決能力を育むのに役立ちます。
グラフ計算機
グラフ計算機は、方程式を解決し、関数のグラフを描くことができます。これにより、関数の変化するパターンを直感的にかつ正確に理解することができます。
グラフ計算機とは？
グラフ計算機は、関数のグラフを描き、複雑な計算を行い、データ分析を行うための強力で技術的に先進的なツールです。グラフィックの変換に影響を与えるパラメータを調整することで、数学の学習と研究がより直観的、効率的、そして興味深くなります。
複雑な手動プロットを置き換える
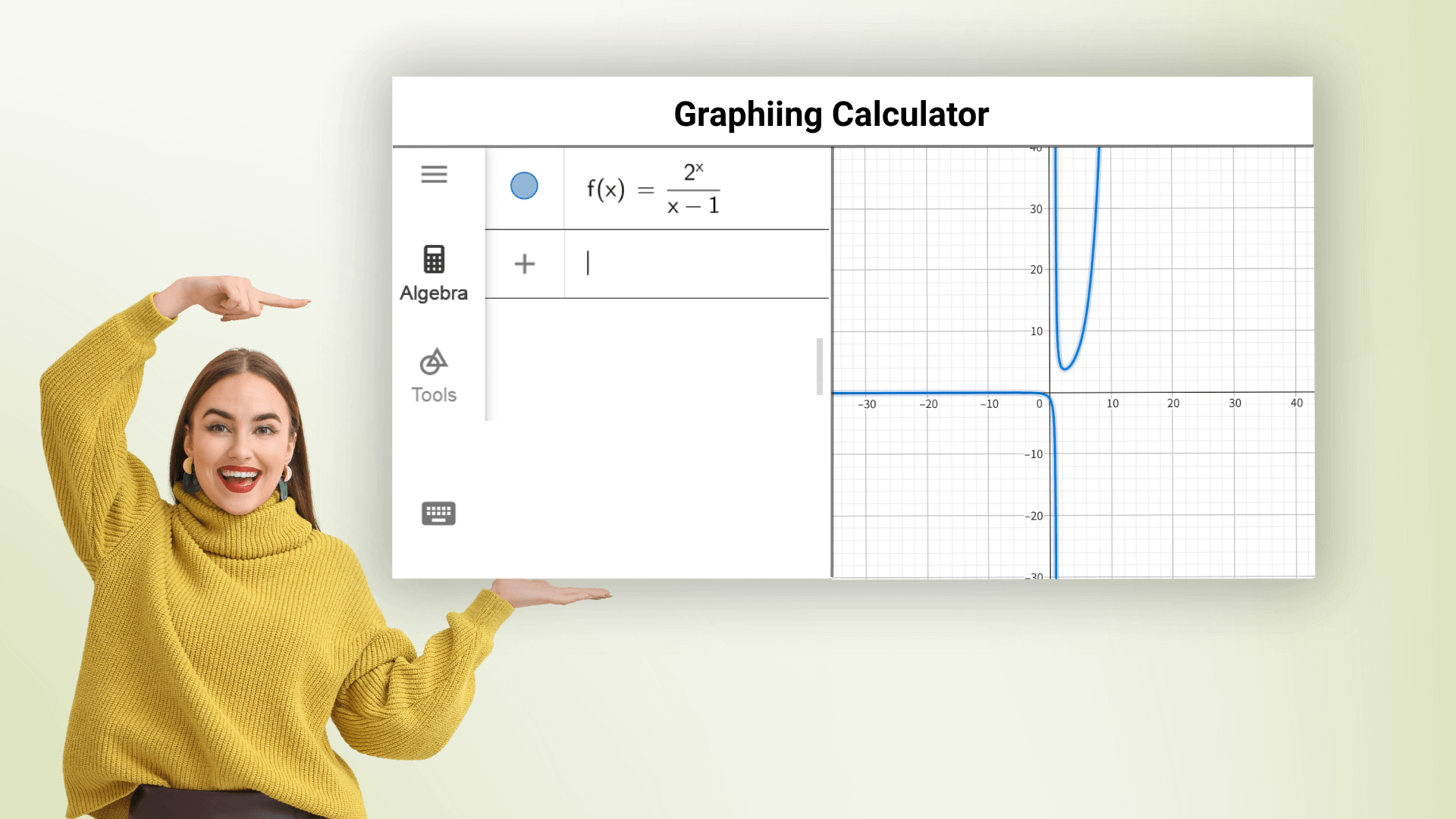
グラフ計算機は、線形、放物線、三角関数、対数関数など、多くの関数のグラフをプロットできます。また、異なる色で複数の方程式を一度にグラフ化することもできます。関数の式を入力するだけで、正確なグラフを素早く取得し、関数の傾向と特徴を観察できます。オンライングラフ計算機は、数学をマスターするための手助けとなり、複雑な計算を避けることを助けます。
豊富な科学計算方法
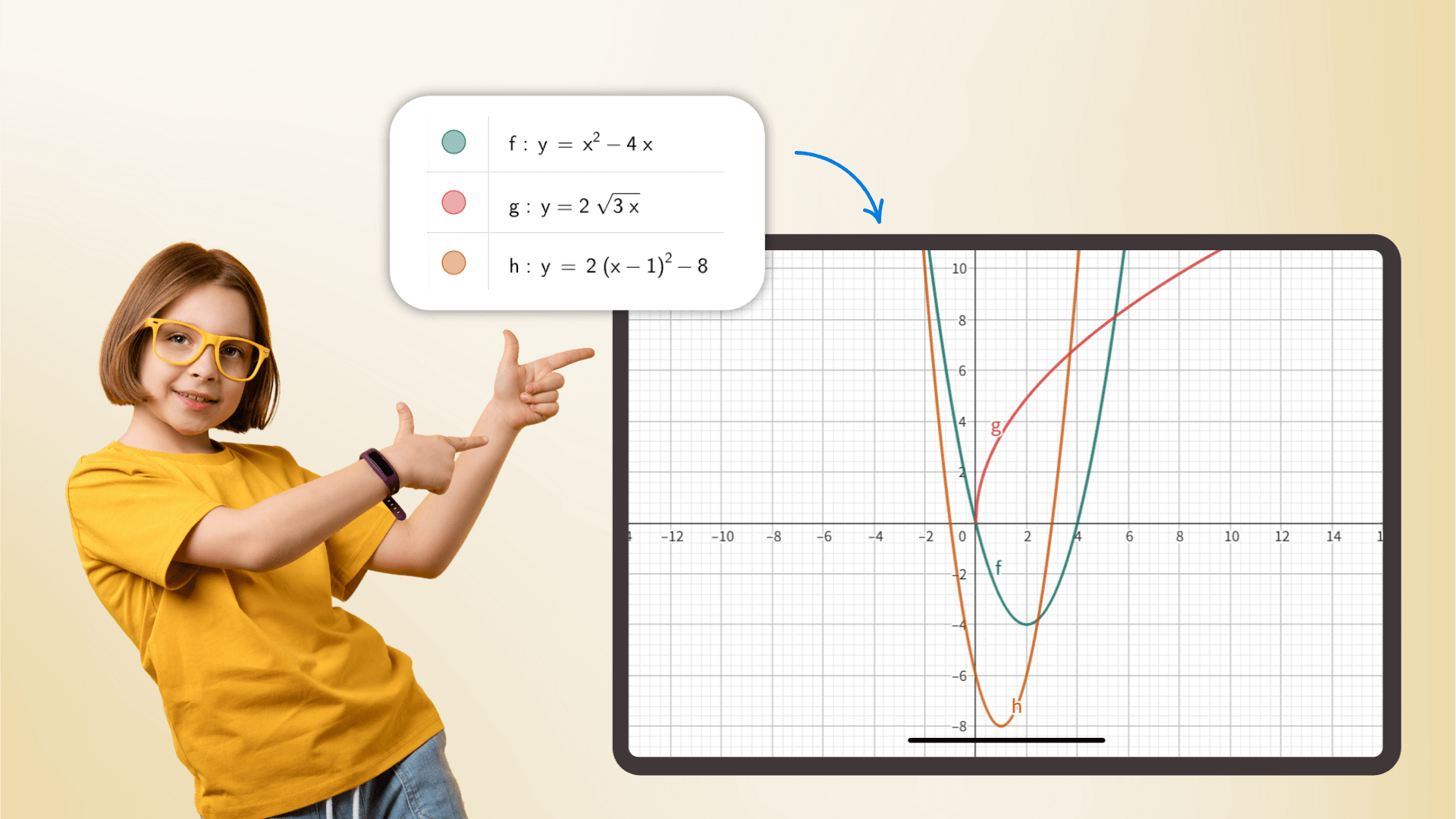
科学計算機として、基本的な算術から高度な数学、微積分、確率統計など、すべてを扱います。精度に基づいた計算により、学生と研究者にとって、学術的・職業的な文脈での効率を高めるための不可欠なアシスタントです。
インテリジェントなインタラクティブ描画
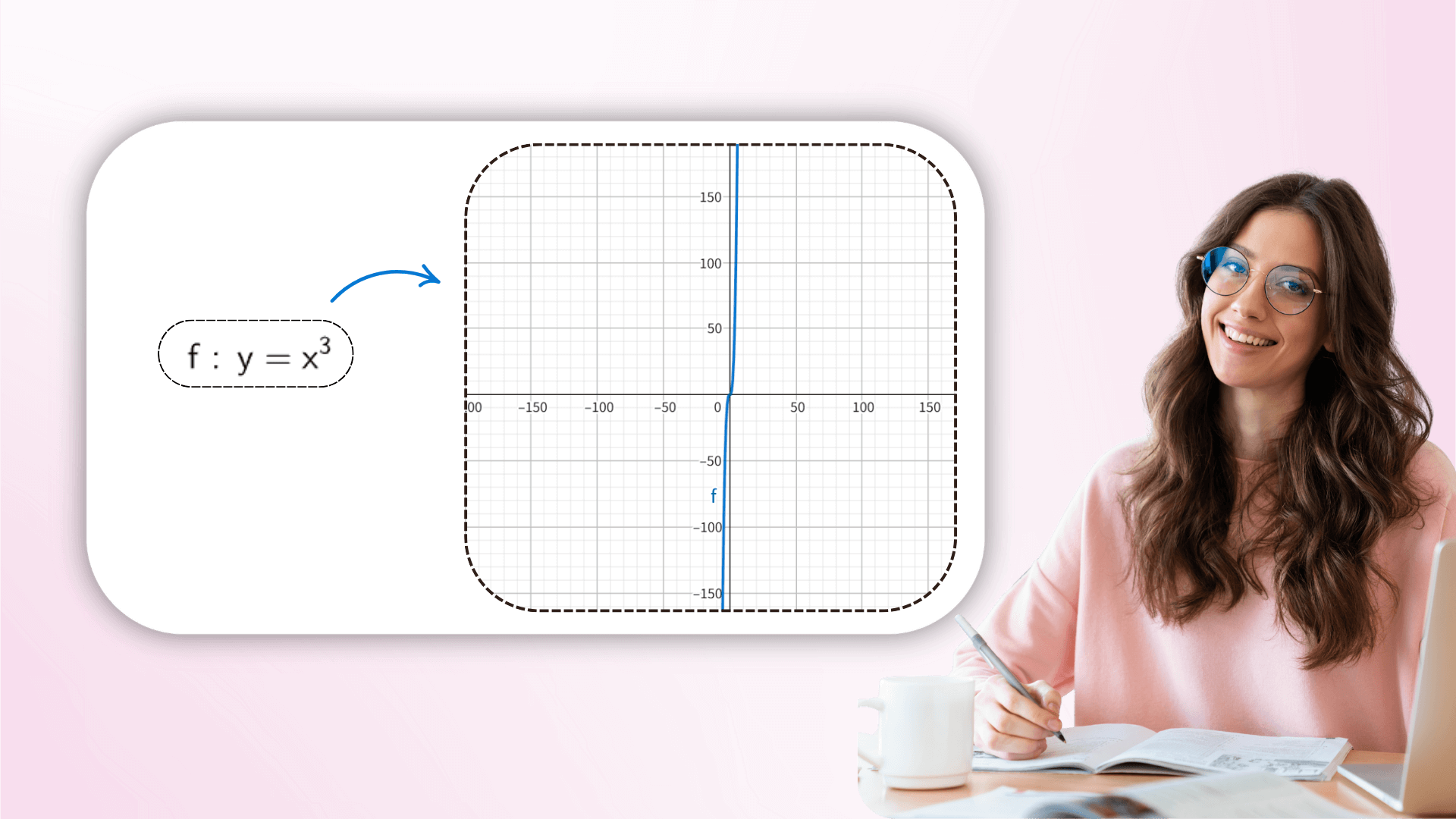
パラメータ値をリアルタイムで調整することで、ユーザーは画像の動的な変換を観察し、係数が関数の幾何学に与える影響を理解できます。線形変換から複雑な変換まで、抽象的な式と視覚をリンクすることで、数学方程式の理解を深めることができます。
グラフ計算機の特徴
インタラクティブな描画
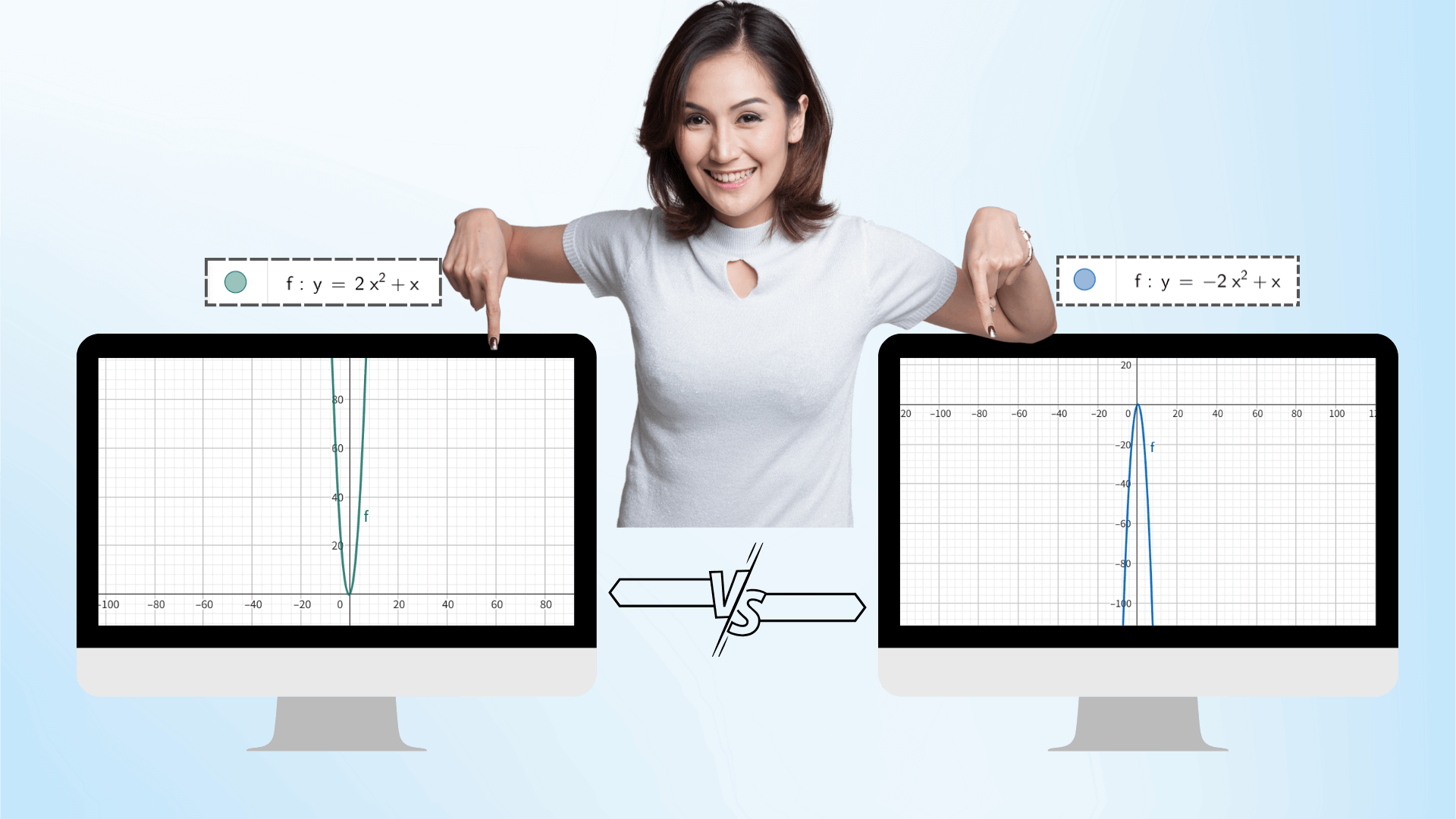
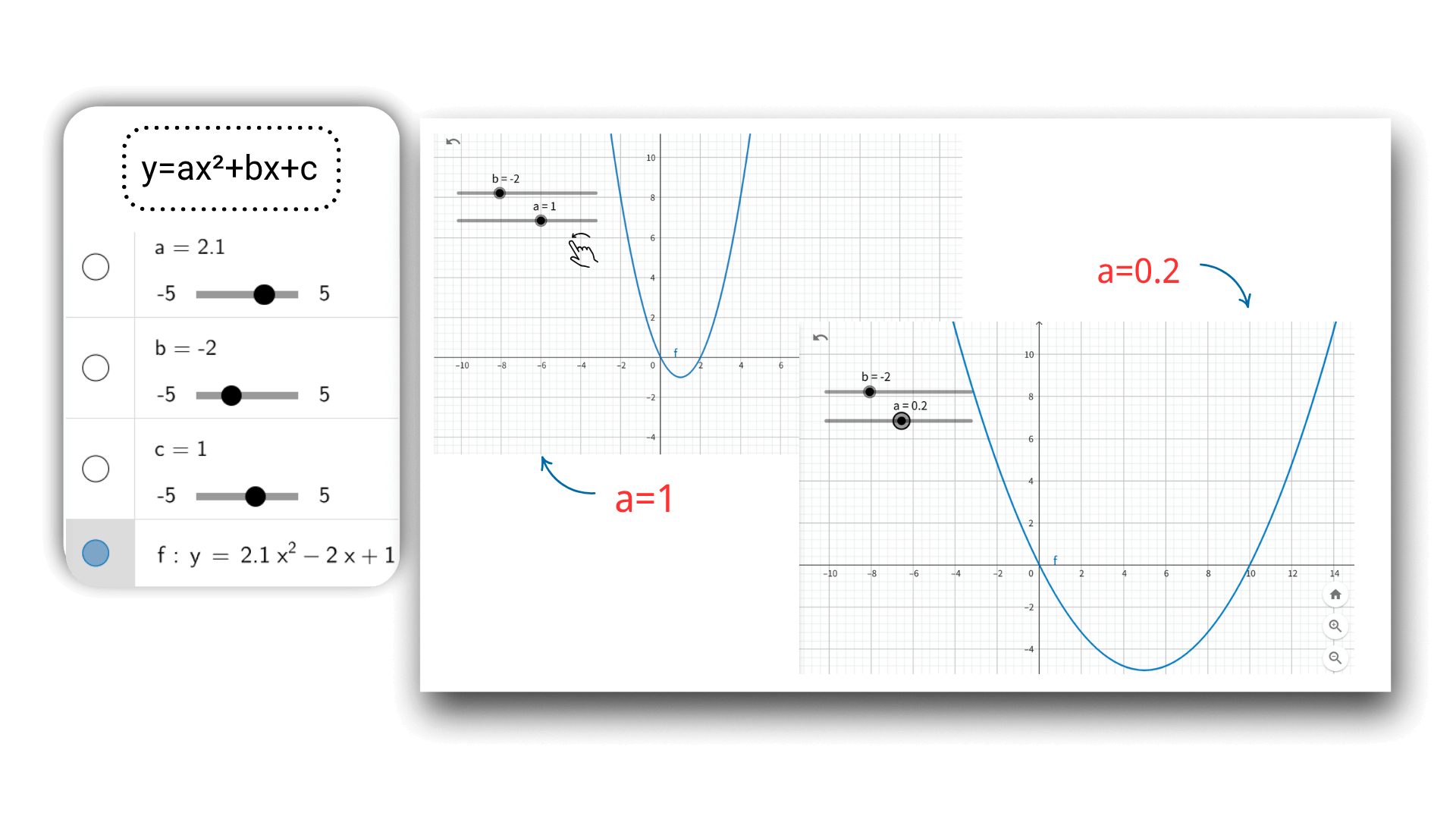
AIグラフ技術を使用して、関数を入力した後、スライダーを通じてパラメータを動的に調整できます。例えば、二次関数のa、b、cなど。画像はアニメーションのようにリアルタイムで変形し、座標データも同時に更新され、パラメータの変更が画像に与える影響を直観的に明らかにし、数学的概念との関係をより理解することができます。
インテリジェントなデータ分析
高度な計算アルゴリズムを採用しており、計算結果の精度が非常に高いため、数学的な仕事に対する信頼できるデータサポートを提供します。画像計算機に配列を入力するだけで、クリック一つで様々な画像を生成できます。
自動的なエラー修正と提案
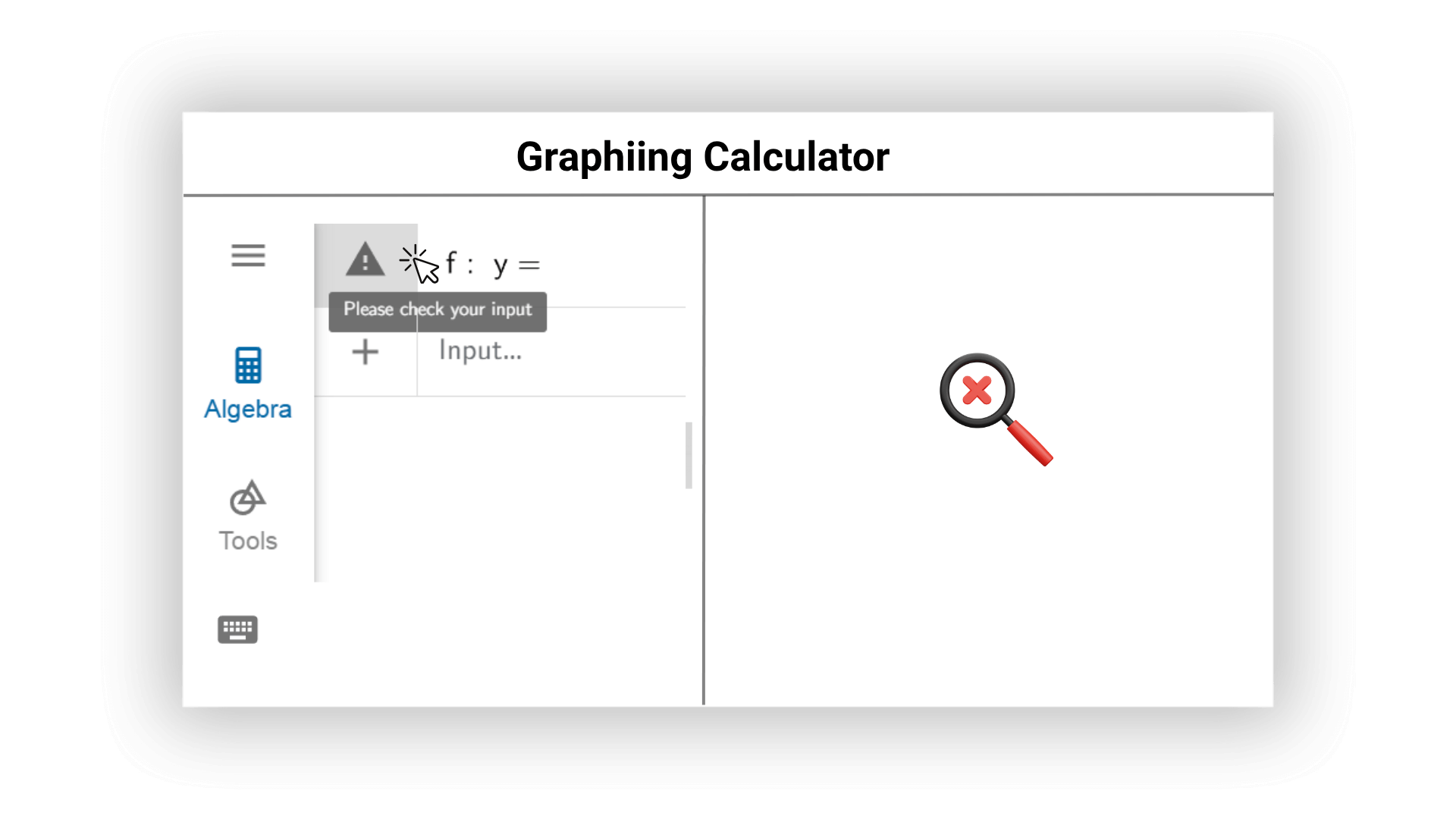
AIグラフ計算機は、数学的な式のオンラインでの可能なエラーをリアルタイムでチェックし、修正の提案を積極的に行います。AIは文法的な問題や不合理的な入力をユーザーに速やかに通知し、計算結果と計算効率の高さを確保し、画像や結果でのエラーを避けることを助けます。
グラフ計算機の使用方法
Step 1
数学式を入力
指定された領域に関数式や分析するデータを入力し、AIグラフ計算機が即座に処理を開始します。
Step 2
グラフを表示
計算やグラフ描画を実行した後、生成された画像、データ、結果を即座に表示できます。
Step 3
グラフと対話
パラメータを調整したり、さらなる分析を行ったりすると、グラフがリアルタイムで更新されます。
クラシックグラフの作図ガイド
一次方程式のパラメータ
二次多項式
多項式のパラメータ
連立一次方程式
導関数のグラフ化
サイン関数の微分
一次不等式
数列の操作
整数の加法の可視化
かけ算の可視化
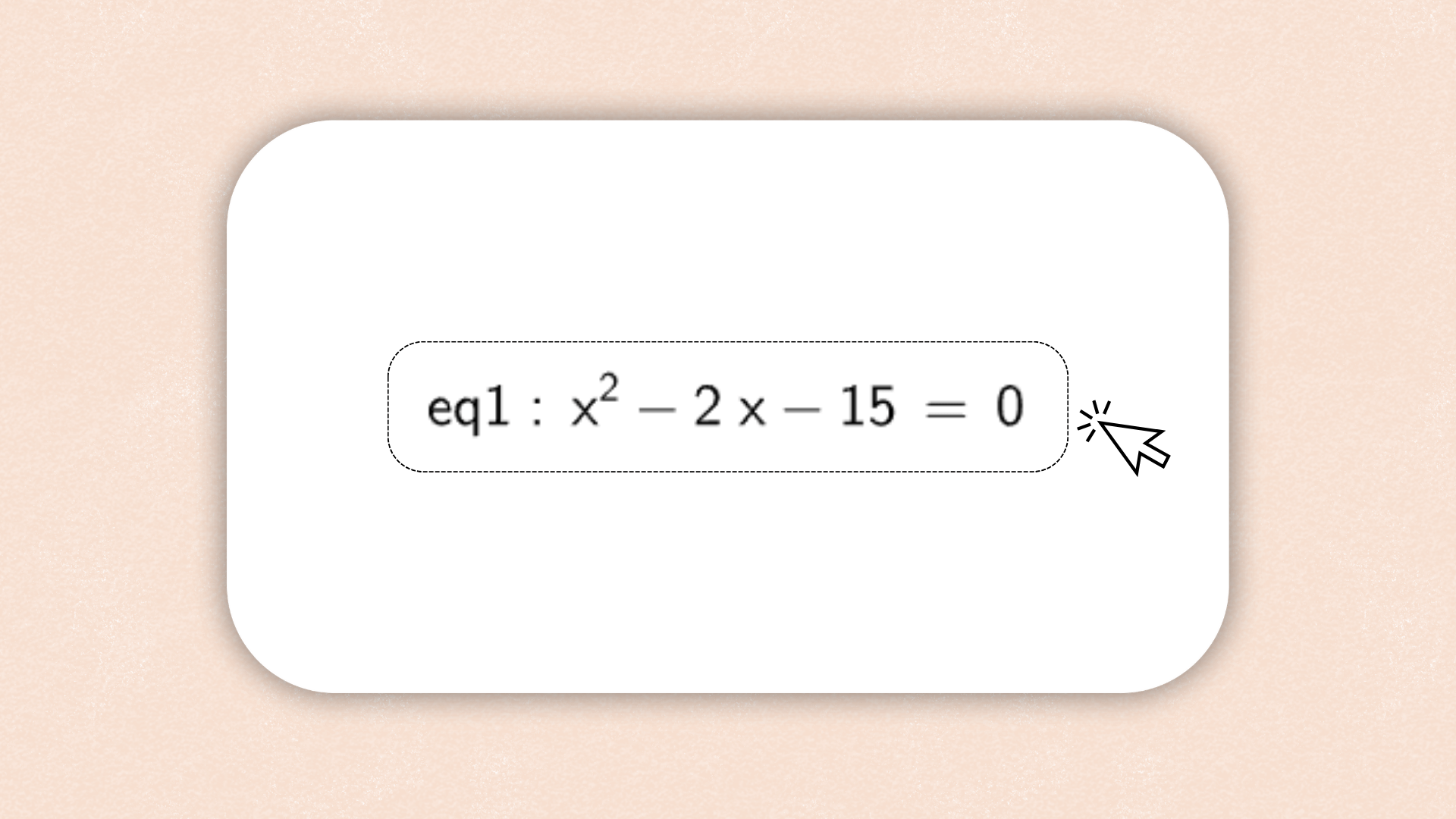
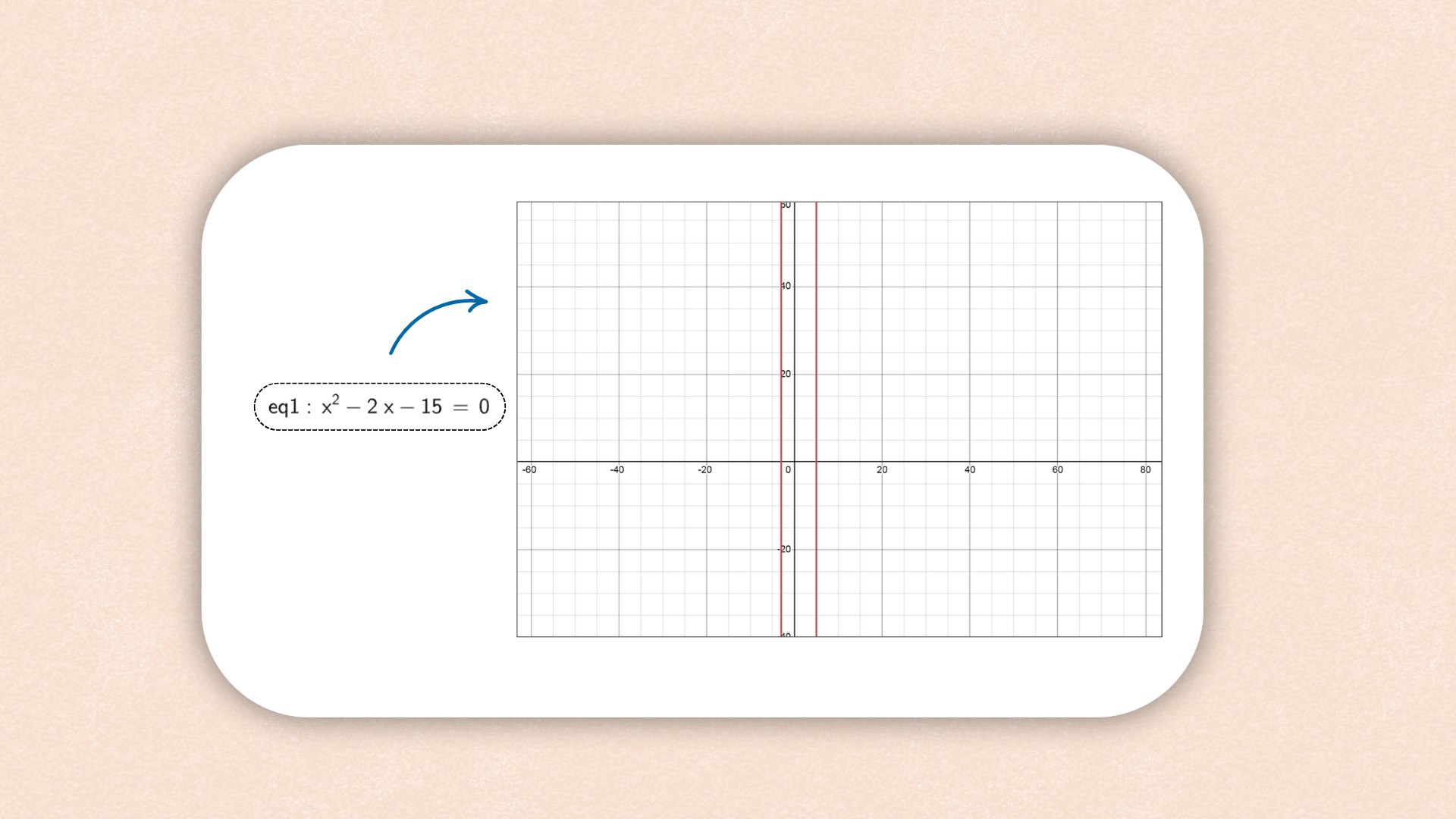
1. 
y = m x + b
を入力バーに入力し、Enterキーを押します。
ヒント：
Enterを押すと、グラフ計算機が自動的にmとbのスライダーを作成します。グラフィックスビューでスライダーを表示するには、代数ビューの変数の左側にある非表示の可視性ボタンを選択してください。
2. 
直線とy軸の交点Aを作成します。
ヒント：
ツールボックスの交点ツールを使って2つのオブジェクトを選択するか、コマンドIntersect(f,
yAxis)を使用できます。
3. 交点ツールを使い、2つの軸を選択して原点に点Bを作成します。
4. 
ツールボックスから線分ツールを選択し、A点とB点を選択して線分を作成します。
ヒント：
または、コマンドSegment(A, B)も使用できます。
5. 
代数ビューの座標の左側にある可視性ボタンをクリックして、A点とB点を非表示にします。
6. 
計測ツールボックスの傾きツールを使い、直線をクリックして傾き（三角形）を作成します。
7. 
スタイルバーを使って作図の見た目を調整します（例：線分の太さを増やしてy軸上で目立たせるなど）。
1. 入力バーにf(x) = x^2と入力し、Enterキーを押します。
この関数グラフはどのような形になりますか？
2. 
移動ツールを使って関数を選択します。スタイルバーをクリックし、関数の固定を解除します。これでグラフィックスビューで関数をドラッグでき、代数ビューの式がどのように変化するか確認できます。
3. 
関数グラフを次の式に合わせて変更します：
f(x) = (x + 2)²
f(x) = x² - 3
および
f(x) = (x - 4)² + 2。
4. 多項式の式を選択し、キーボードでf(x) = 3 x^2に変更します。
グラフはどのように変化しますか？
5. パラメータに異なる値（例：0.5、-2、-0.8、3）を入力して式の変更を繰り返します。
1. 
入力バーにf(x) = a*x³ + b*x² + c*x + dと入力し、Enterキーを押します。
ヒント：
グラフ計算機が自動的にa、b、c、dのスライダーを作成します。
2. 代数ビューの該当エントリの左側にある非表示の可視性ボタンを選択して、グラフィックスビューでスライダーを表示します。
3. グラフィックスビューのスライダーを使い、移動ツールでパラメータの値をa = 0.2, b = -1.2, c = 0.6, d = 2に変更します。
4. 
入力バーにR = Root(f)と入力して多項式の根を表示します。根は自動的にR1、R2、R3と名付けられます。
5. 
E = Extremum(f)と入力して多項式の極値を表示します。
6. 
接線ツールを使い、極値E1とE2を通る多項式の接線を作成します。
ヒント：
特殊な直線ツールボックスを開き、接線ツールを選択します。E1点と多項式を順に選択して接線を作成し、E2点でも繰り返します。
7. 移動ツールでスライダーの値を系統的に変えて、パラメータが多項式にどのように影響するかを探ります。
1. 入力バーに一次方程式line_1: y = m_1 x + b_1を入力します。
ヒント：
line_1と入力するとline1が作成されます。
2. 
Enterを押すと、グラフ計算機がm_1とb_1のスライダーを自動的に作成します。
3. 代数ビューのエントリの横にある非表示の可視性ボタンをクリックして、グラフィックスビューでスライダーを表示します。
4. line_2: y = m_2 x + b_2の式についても1～3の手順を繰り返します。
5. スタイルバーを使って2本の直線とそのスライダーの色を変更します。
6. 
テキストツールを使い、ダイアログにLine 1:と入力し、オブジェクトタブのリストからline_1を選択して動的テキストを作成します。
7. 静的部分Line 2:とline_2を選択して動的テキストを作成します。
8. スタイルバーを使い、テキストの色を対応する直線の色と合わせます。
9. line_1とline_2の交点Aを、交点ツールを使うか、入力バーにIntersect(line_1, line_2)と入力して作成します。
10. 入力バーにxcoordinate = x(A)と入力します。
ヒント： x(A)は交点Aのx座標を取得します。
11. ycoordinate = y(A)も定義します。
ヒント： y(A)は交点Aのy座標を取得します。
12. 静的部分Solution: x =とxcoordinateを選択して動的テキストを作成します。
13. 静的部分y =とycoordinateを選択して動的テキストを作成します。
14. テキストを選択し、スタイルバーを開いて誤って移動しないように固定します。
1. 入力バーに多項式f(x) = x^2/2 + 1を入力します。
2. 
関数f上に新しい点Aを作成します。
ヒント： 点Aは関数上のみ移動できます。
3. 点Aを通る関数fの接線gを作成します。
4. 接線gの傾きをm = Slope(g)で作成します。
5. 点S = (x(A), m)を定義します。
ヒント： x(A)は点Aのx座標です。
6. 点AとSを線分で結びます。
7. 
点Sのトレースをオンにし、点Aを動かします。
ヒント： 点Sを右クリック（MacOS:
Ctrlクリック、タブレット:
長押し）し、「トレースを表示」を選択します。
1. 入力バーに関数f(x) = sin(x)を入力します。
2. 
グラフィックスビューを右クリックし、「グラフィックス...」を選択します。x軸タブを選択し、単位をπに変更します。
3. 関数f上に新しい点Aを作成します。
ヒント： 点Aは関数上のみ移動できます。
4. 点Aを通る関数fの接線gを作成します。
5. 傾きツールを使って接線gの傾きを作成します。
6. 点S = (x(A), m)を定義します。
ヒント： x(A)は点Aのx座標です。
7. 点AとSを線分で結びます。
8. 点Sのトレースをオンにし、点Aを動かします。
ヒント： 点Sを右クリック（MacOS:
Ctrlクリック、タブレット:
長押し）し、「トレースを表示」を選択します。
9. 点Aを右クリック（MacOS: Ctrlクリック、タブレット:
長押し）し、コンテキストメニューからアニメーションを選択します。
ヒント：
グラフィックスビュー左下にアニメーションボタンが表示され、アニメーションの一時停止や再開ができます。
1. 入力バーにa x + b y ≤ cと入力し、Enterキーを押します。
ヒント：
バーチャルキーボードで≤記号を入力できます。グラフ計算機が自動的にa、b、cのスライダーを作成します。
2. 移動ツールでスライダーの値をa = 1、b = 1、c =
3に調整します。
3. スライダーの増分を1に変更します。
ヒント：
数値aを選択し、グラフィックスビューのスタイルバーを開きます。
数値aの設定を開き、スライダータブを選択します。
増分を1に設定し、bとcについても繰り返します。
4. グラフィックスビューの背景をドラッグして原点を中央に移動します。
5. 
ズームアウトして座標系のより広い範囲を画面に表示します。
6. 軸の目盛りの間隔を1に設定します。
ヒント：
グラフィックスビューのスタイルバーを開く前に、オブジェクトが選択されていないことを確認してください。
軸の設定を開きます。
x軸タブを選択し、間隔を1に設定します。
y軸タブでも繰り返します。
1. 入力バーにSequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5)と入力し、Enterキーを押します。
2. 1から10まで、増分1の数値用スライダーsを作成します。
3. 入力バーにSequence((i, i), i, 0, s)と入力し、Enterキーを押します。
4. スライダーsを動かして作図を確認します。
1. スタイルバーを使ってグラフィックスビューの設定を開きます。
2. x軸タブで目盛りの間隔を1に設定します（距離のボックスにチェックを入れ、テキストフィールドに1を入力）。
3. 基本タブでx軸の最小値を-11、最大値を11に設定します。
4. y軸タブで「y軸を表示」をオフにし、設定を閉じます。
5. 区間-5～5、増分1の2つのスライダーaとbを作成します。
6. 
スタイルバーを使い、スライダー名の代わりに値を表示します。
7. A = (0, 1)とB = A + (a, 0)の点を作成します。
ヒント：
B点とA点の距離はスライダーaで決まります。
8. 
u = Vector(A, B)という長さaのベクトルを作成します。
9. C = B + (0, 1)とD = C + (b, 0)の点を作成します。
10. v = Vector(C, D)という長さbのベクトルを作成します。
11. R = (x(D), 0)の点を作成します。
ヒント：
x(D)はD点のx座標を取得します。R点は数直線上で加算の結果を示します。
12. Z = (0, 0)の点を作成します。
13. 3つの線分c = Segment(Z, A)、d = Segment(B, C)、e = Segment(D, R)を作成します。
14. スタイルバーを使って作図を調整します（例：スライダーとベクトルの色を合わせる、線種を変更、スライダーを固定、ラベルや点を非表示など）。
1. 区間1～10、増分1、幅300の数値用水平スライダーColumnsを作成します。
ヒント：
スライダーの幅は設定タブのスライダーで変更できます。
2. 
新しい点Aを作成します。
3. 
点Aから始まる長さColumnsの線分fを作成します。
4. Columnsスライダーを動かして指定した長さの線分を観察します。
5. 
点Aを通る線分fの垂線gを作成します。
6. 点Bを通る線分fの垂線hを作成します。
7. 区間1～10、増分1、幅300の数値用垂直スライダーRowsを作成します。
ヒント：
スライダーの向きはスライダーダイアログのスライダータブで選択できます。
8. 
中心A、半径Rowsの円cを作成します。
9. Rowsスライダーを動かして指定した半径の円を観察します。
10. 円cと直線gの交点Cを作成します。
ヒント：
交点ツールを選択したら、A点の上の交点をクリックしてこの点だけを作成します。
11. 
交点Cを通る線分fに平行な直線iを作成します。
12. 直線iとhの交点Dを作成します。
13. 
多角形ABDCを作成します。
14. 
すべての直線、円c、線分fを非表示にします。
15. スタイルバーを使って線分のラベルを非表示にします。
16. ColumnsとRowsの両方のスライダーを値10に設定します。
17. 次の式で縦の線分のリストを作成します：Sequence(Segment(A + i*(1, 0), C + i*(1, 0)), i, 1,
Columns)
注：A + i*(1,
0)はA点から始まり1ずつ離れた点の列を指定します。
C +
i*(1, 0)はC点から始まり1ずつ離れた点の列を指定します。
Segment(A
+ i*(1, 0), C + i*(1,
0))はこれらの点のペア間の線分リストを作成します。線分の端点はグラフィックスビューには表示されません。
スライダーColumnsが線分の数を決定します。
18. 横の線分のリストを作成します。Sequence(Segment(A + i*(0, 1), B + i*(0, 1)), i, 1,
Rows)
19. ColumnsとRowsのスライダーを動かして作図を観察します。
20. ColumnsとRowsの値を使ってかけ算の問題を表す静的・動的テキストを挿入します：text1: Columnstext2: *text3: Rowstext4: =
21. かけ算の結果を計算します：result = Columns * Rows
22. 動的テキスト5：resultを挿入します。
23. 点A、B、C、Dを非表示にします。
24. スタイルバーを使って作図を調整します。
グラフ計算機の適用シナリオ
数学教育
AIグラフ計算機は、学生が数学を学ぶための強力なアシスタントです。中学校から大学まで、代数、幾何、微積分、統計など、数学の知識をより理解し、マスターすることを助け、学習効率と成績を向上させることができます。教師はこれを使用して、教示を行い、生徒の学習意欲と熱意を刺激するための生動的な教材を作成できます。
科学研究
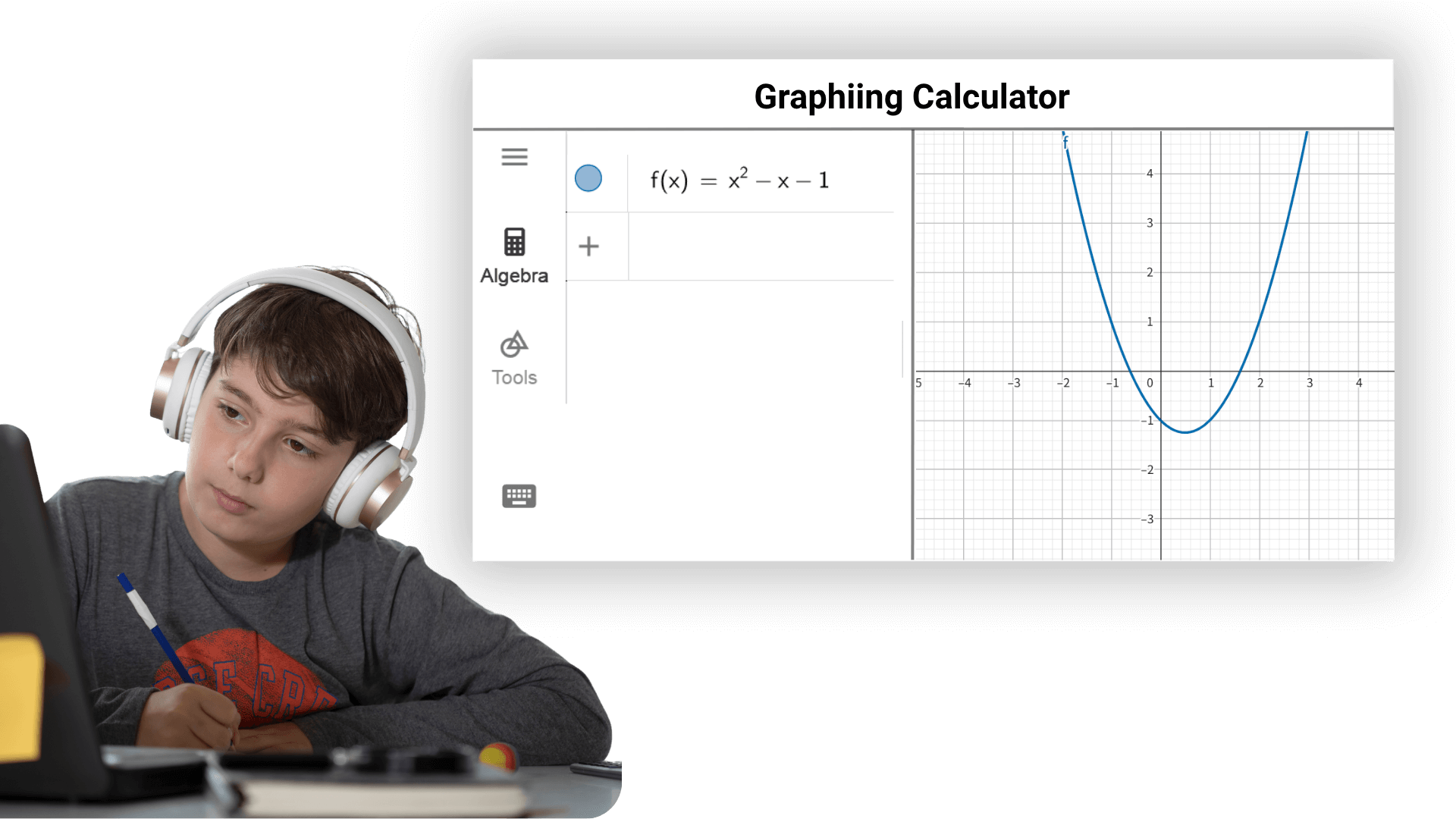
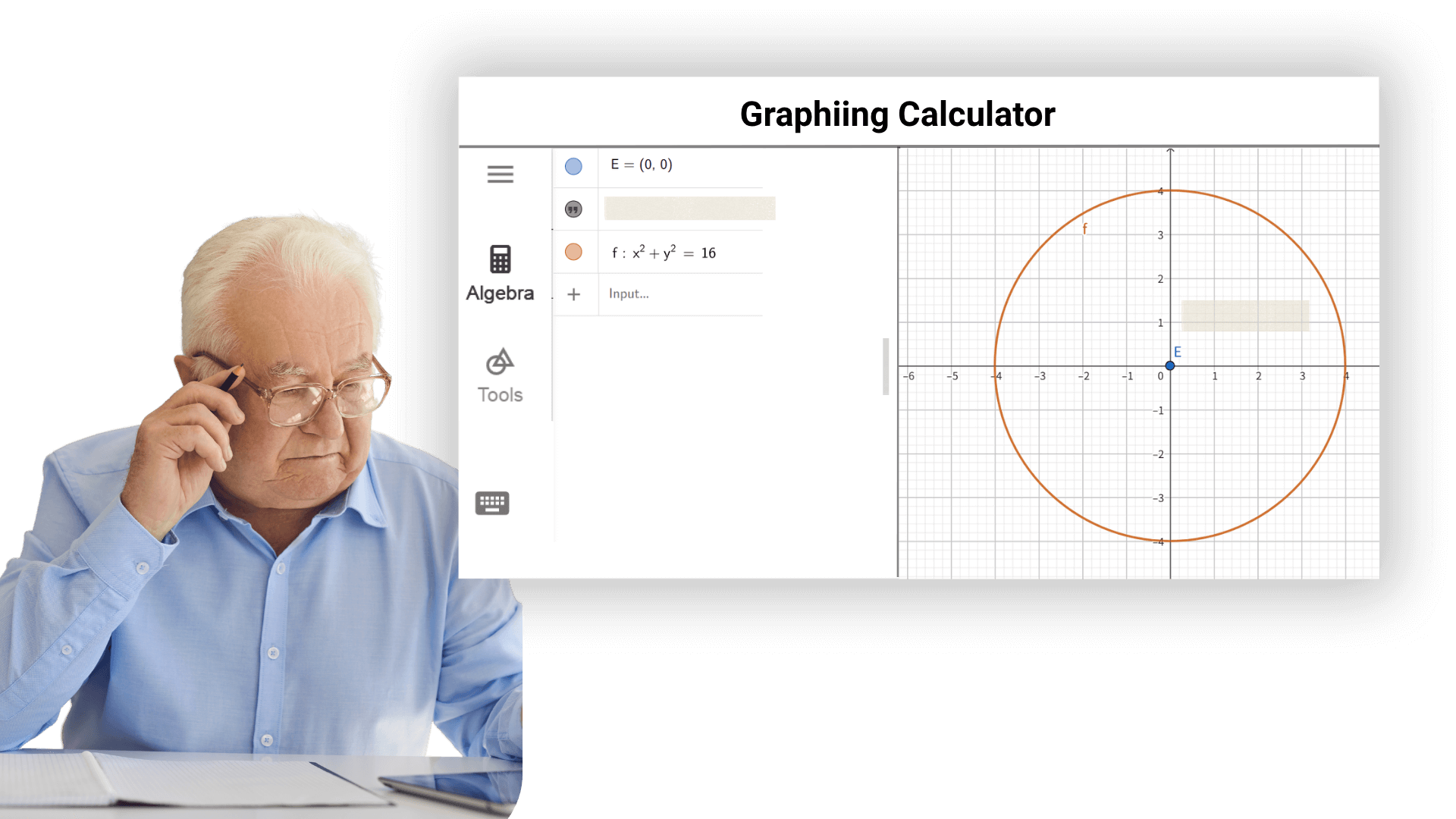
これは、研究者がデータ処理、実験分析、モデル構築、理論検証を行うための強力な数学ツールを提供します。物理、化学、生物学、工学など、科学の多くの分野で、グラフィック計算機は複雑な数学操作とデータ分析を迅速かつ正確に完了することを助け、科学研究のスムーズな発展を支援します。
ビジネスとデータ分析
グラフ計算機を使用して、供給と需要の曲線、複利成長モデルなどを描き、辺際費用と収入関数の交点を分析し、ビジネスでの意思決定を支援します。
誰が当社のグラフ計算機を使用できますか？
- 学生
- 教師
- 研究者
- データアナリスト
- ソフトウェアエンジニア
- デザイナー
教師
数学教師は、グラフ計算機を使用して授業資料を作成し、概念や問題解決プロセスをデモンストレーションすることで、教育効果と相互作用を向上させます。
研究者
さまざまな分野の研究者は、複雑な数学計算とデータ分析に依存しています。オンラインのグラフ計算機は、正確な結果を迅速に生成し、研究を加速します。
データアナリスト
手間のかかる手動描画をおさらばし、クリック一つで専門的なデータ可視化チャートを生成し、オンラインで関数グラフを描画し、リアルタイムで平均と分散を注釈し、回帰曲線を動的にフィットし、データの統合と分析を効率的に完了します。
ソフトウェアエンジニア
グラフ計算機は、ソフトウェアエンジニアがフィルタアルゴリズムを視覚化し、レンダリングパラメータを最適化し、ピクセルパーフェクトな機能パフォーマンスを確保するのに役立ちます。
建築デザイナー
建築デザイナーにとって、グラフ計算機はパラメトリックデザインの強力なツールです。曲線方程式を入力して、関数/変位グラフを生成し、構造力学を視覚的に検証し、設計サイクルを短縮します。
Decopyのグラフ計算機の機能性の利点
完全に無料で使用できます
すべての機能は登録や支払いが必要なく、いつでも使用できます。
高精度のアルゴリズム
行列式の行列式や積分などの高度な問題を計算する際には、高精度を維持して科学研究の誤りを避ける必要があります。
データのプライバシーとセキュリティ
計算は完全にブラウザ内で完了し、データはアップロードされず、ページを閉じるとクリアされます。
いつでも利用可能
ダウンロードやインストールが必要なく、スマートフォンやコンピュータで直ちに使用できます。
広告の割り込みなし
学習の本質に集中し、ポップアップや広告がなく、集中力を向上させることができます。
全シナリオサポート
学術、科学研究、オフィス、エンジニアリングアプリケーションなど、グラフィック計算のニーズに応えられます。
Decopyグラフ計算機のユーザーレビュー
Sarah Johnson
大学生
Robert Thompson
数学教師
David Wilson
金融アナリスト
よくある質問（FAQ）
登録やソフトウェアのダウンロードは必要ありません。ブラウザで当社のウェブサイトを入力し、この強力なグラフ計算機ツールを使用し始めることができます。その便利さを即座に体験できます。
はい、当社のAIグラフ計算機は完全に無料です。無料であるにもかかわらず、いかなるコア機能も制限しません。グラフ描画、計算、データ解析機能を全て無料でフルに利用できます。誰もが便利で効率的な数学ツールを提供することを目指しています。
私たちはあなたのデータのセキュリティとプライバシーを最優先に考えています。あなたの計算、グラフ、入力データはすべてあなたのブラウザでローカルに処理され、私たちのサーバーにアップロードされることはありません。あなたのデータが安全であることを知って、安心して使用できます。
関数を入力するには、ホームページの入力ボックスに式を入力するだけです。例えば、「y=2x^2」や「f(x)=sin(x)」を入力します。計算機は自動的にあなたの入力を処理し、グラフを表示します。
はい、AIグラフ計算機は、単純な一次方程式から積分、微分、多変数方程式などの高度なものまで、さまざまな関数を扱うことができます。基本的な数学的ニーズから高度なものまで、学生やプロフェッショナルに最適です。
はい、モバイルデバイスで完全にアクセスできます。スマートフォンやタブレットで使用でき、すべての画面サイズに最適化されていますので、どこにいてもシームレスな体験をお楽しみいただけます。
↑