Estudantes
Explore a conexão entre álgebra e geometria, aprofunde a compreensão dos conceitos matemáticos e use a calculadora de geometria para concluir tarefas e projetos.
Calculadora de geometria que desenha figuras geométricas e calcula suas propriedades, fornecendo uma solução eficiente para o aprendizado e a exploração de problemas de geometria.
A calculadora de geometria é uma poderosa ferramenta que integra funções de álgebra, geometria e análise de dados. Ela foi projetada para aprendizagem, ensino e realização de diversos tipos de pesquisas geométricas. A calculadora de geometria online ajuda os usuários a explorar e calcular problemas geométricos de forma mais intuitiva e eficiente.
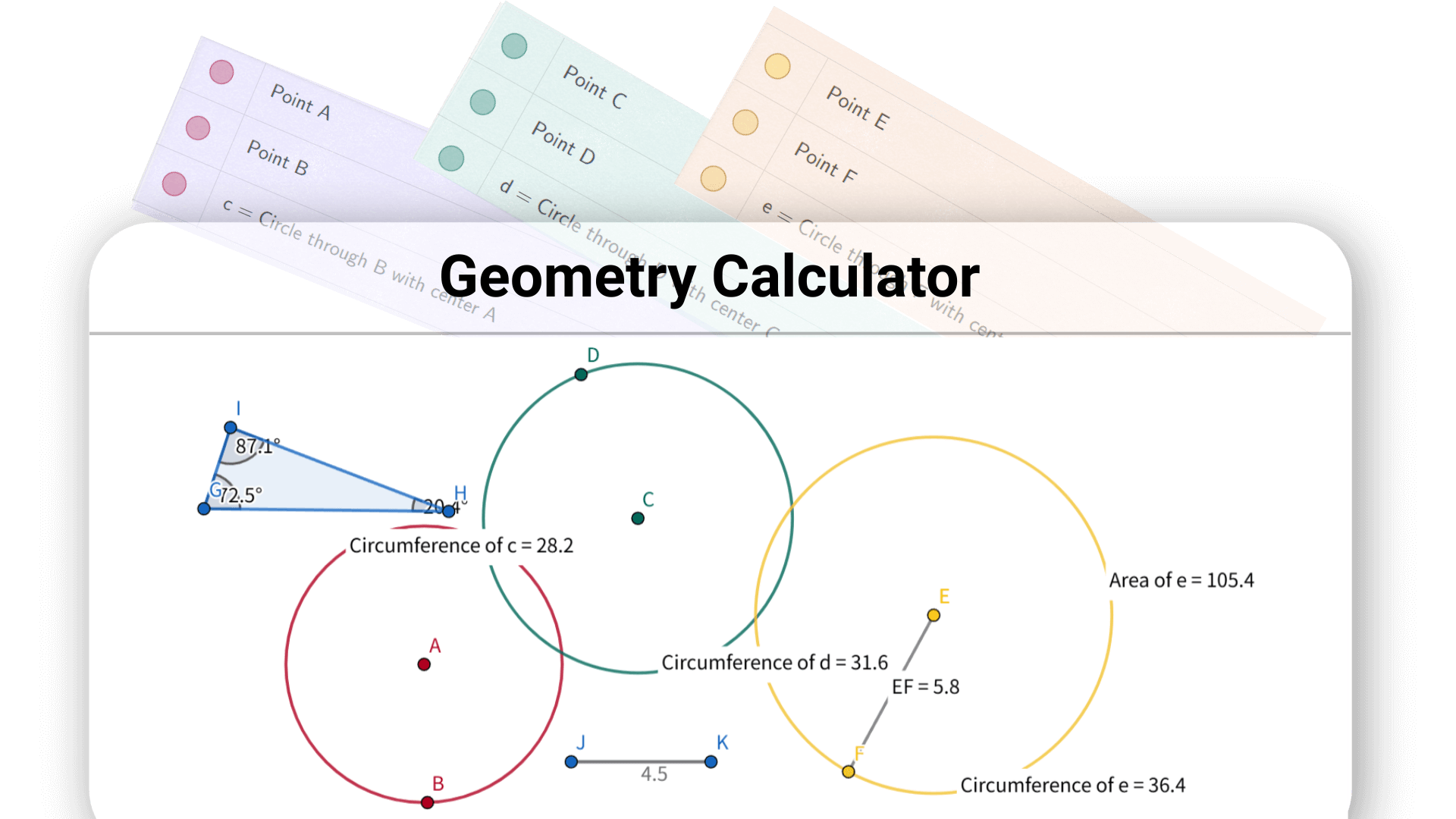
A melhor calculadora de geometria da Decopy pode economizar seu tempo valioso, sem mais folhear livros ou desenhar no papel. Ela permite que você se concentre em entender conceitos geométricos em vez de se perder em cálculos complexos.
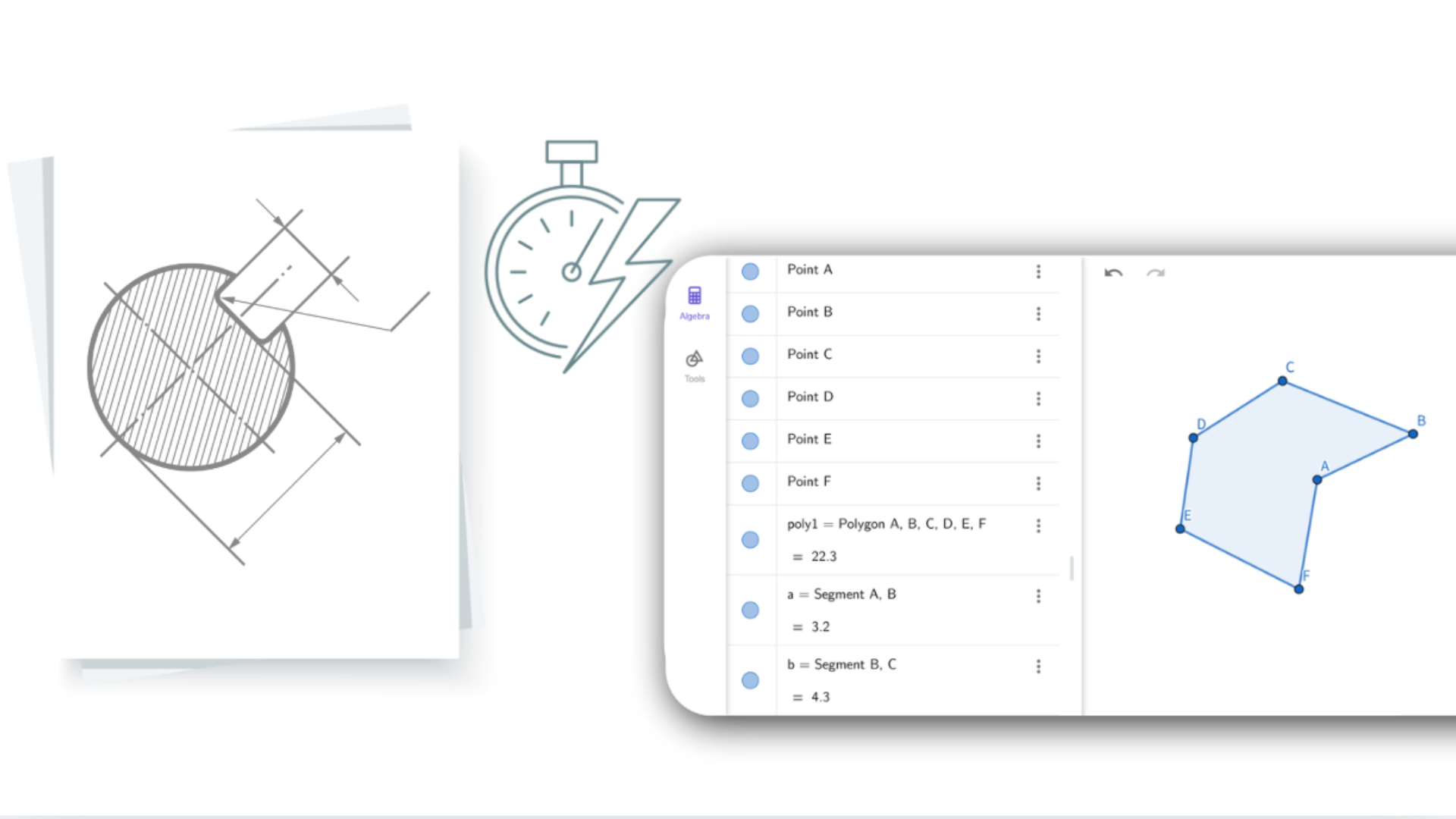
Ao inserir equações ou coordenadas, a calculadora de geometria mostra instantaneamente as formas correspondentes. Ajustar uma figura atualiza as expressões algébricas relacionadas em tempo real. Essa interação dinâmica conecta álgebra e geometria, ajudando os usuários a entender problemas de diferentes ângulos. A calculadora de geometria torna a matemática abstrata visual e mais fácil de compreender.
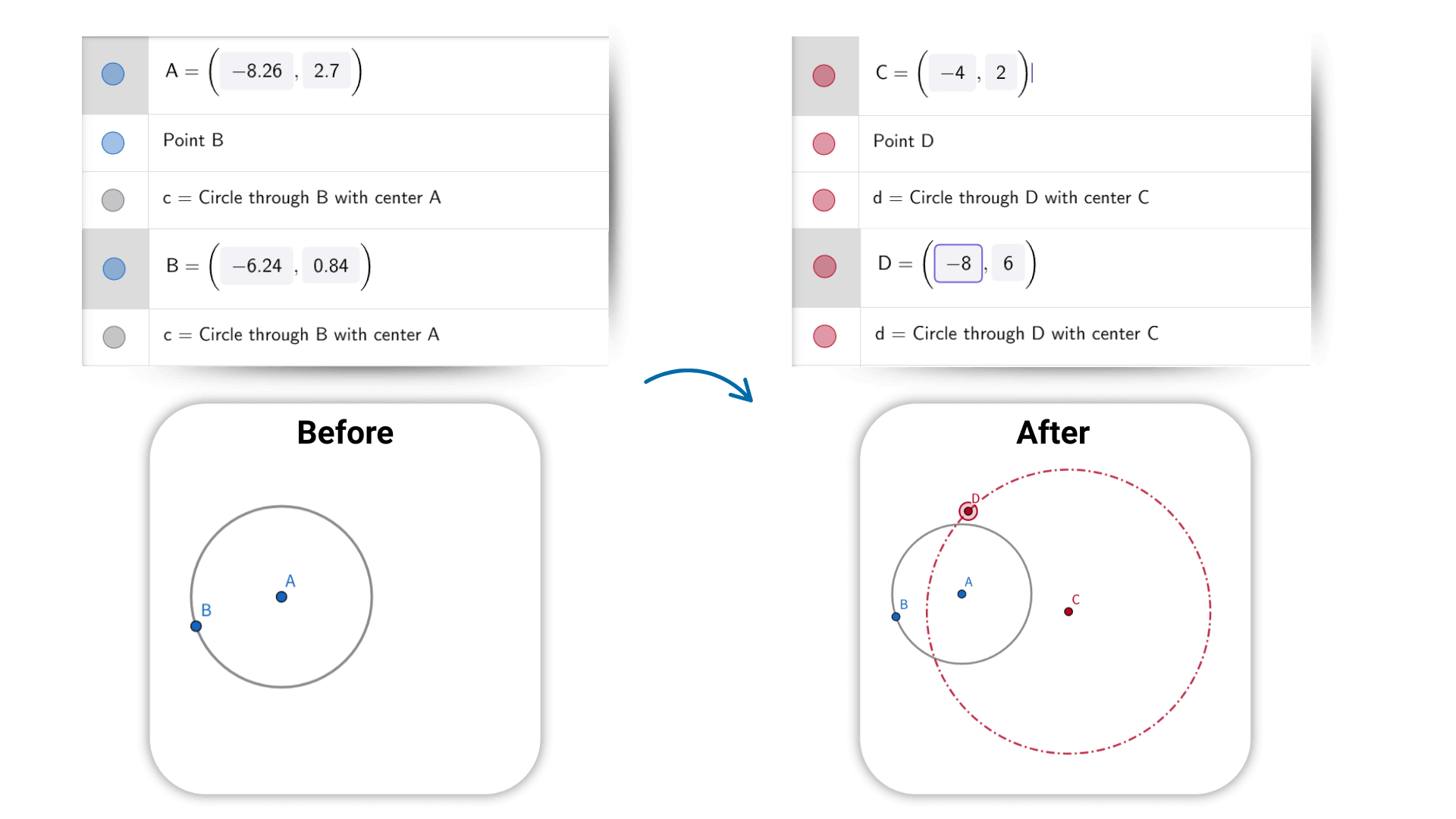
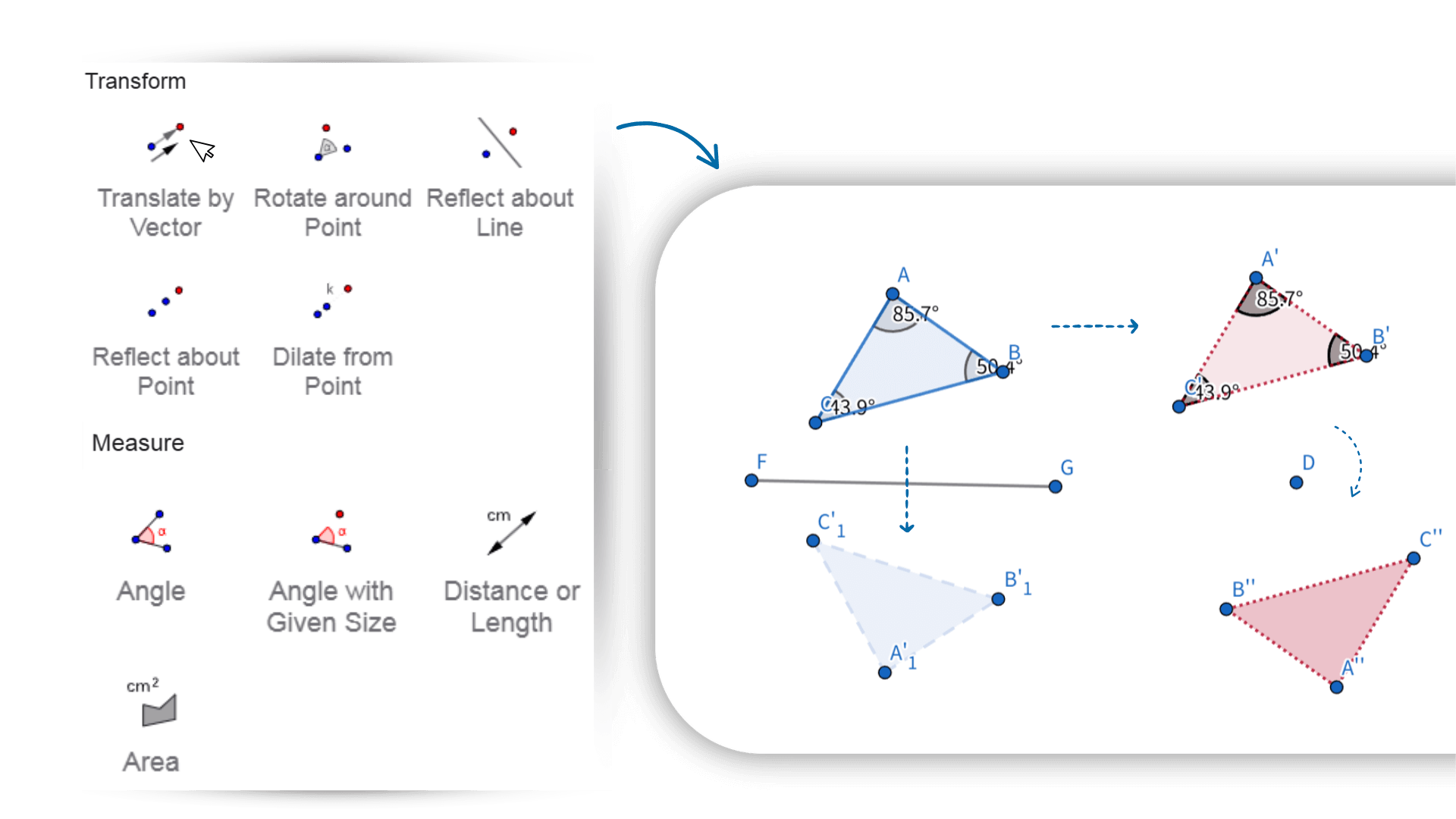
A calculadora de geometria suporta transformações como translação, rotação e escala. Com ações simples, você pode ver as mudanças das formas em tempo real. Figuras, expressões e dados são totalmente interativos—arrastar um ponto ou ajustar um parâmetro atualiza automaticamente as relações e resultados relacionados. Esta calculadora de geometria online ajuda você a explorar como os objetos geométricos se conectam e se comportam, facilitando a compreensão de sua natureza dinâmica.
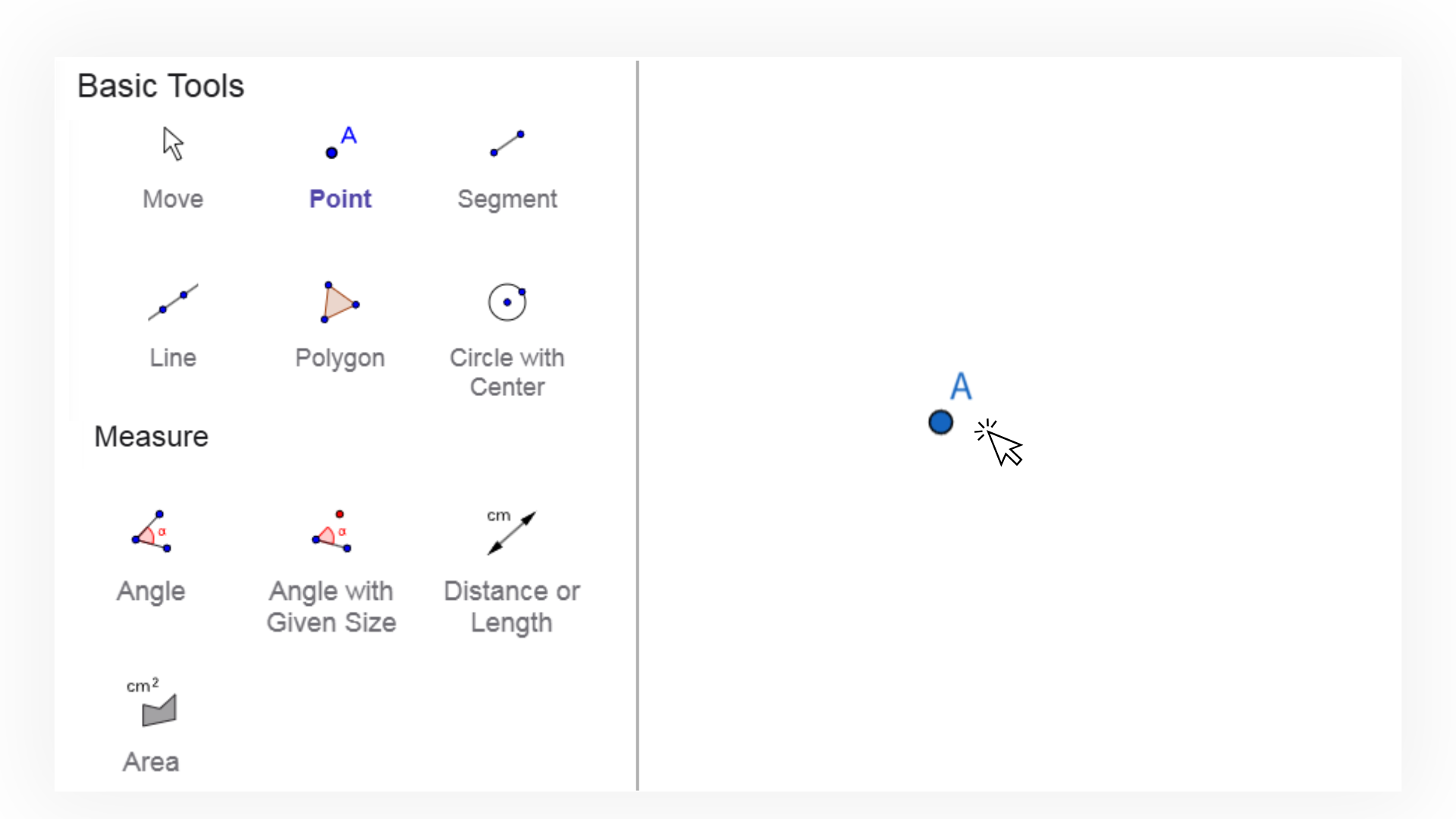
1. ![]() Selecione a ferramenta Reta e crie uma reta arbitrária AB
clicando duas vezes na Visualização Gráfica.
Selecione a ferramenta Reta e crie uma reta arbitrária AB
clicando duas vezes na Visualização Gráfica.
2. ![]() Crie uma reta BC usando novamente a ferramenta Reta.
Crie uma reta BC usando novamente a ferramenta Reta.
Dica:
Selecione o ponto B e depois clique na Visualização Gráfica
para criar o ponto C.
3. ![]() Ative a ferramenta Reta Paralela e crie uma reta paralela à
reta AB passando pelo ponto C.
Ative a ferramenta Reta Paralela e crie uma reta paralela à
reta AB passando pelo ponto C.
Dica: Abra a
Caixa de Ferramentas de Retas Especiais, ative a ferramenta
Reta Paralela e selecione a reta AB e depois o ponto
C.
4. ![]() Crie uma reta paralela à reta BC passando pelo ponto A
usando novamente a ferramenta Reta Paralela.
Crie uma reta paralela à reta BC passando pelo ponto A
usando novamente a ferramenta Reta Paralela.
5. ![]() Selecione a ferramenta Interseção e crie o ponto de
interseção D das duas retas.
Selecione a ferramenta Interseção e crie o ponto de
interseção D das duas retas.
Dica: Abra a Caixa
de Ferramentas de Pontos, ative a ferramenta Interseção e
clique diretamente no ponto de interseção.
6. ![]() Ative a ferramenta Polígono e crie o paralelogramo ABCD
selecionando sucessivamente todos os vértices.
Ative a ferramenta Polígono e crie o paralelogramo ABCD
selecionando sucessivamente todos os vértices.
Nota:
Para fechar o polígono, selecione novamente o primeiro
ponto.
7. ![]() Selecione a ferramenta Mover e arraste os vértices do
paralelogramo para verificar se ele foi construído
corretamente.
Selecione a ferramenta Mover e arraste os vértices do
paralelogramo para verificar se ele foi construído
corretamente.
1. ![]() Crie o segmento AB clicando duas vezes na Visualização
Gráfica.
Crie o segmento AB clicando duas vezes na Visualização
Gráfica.
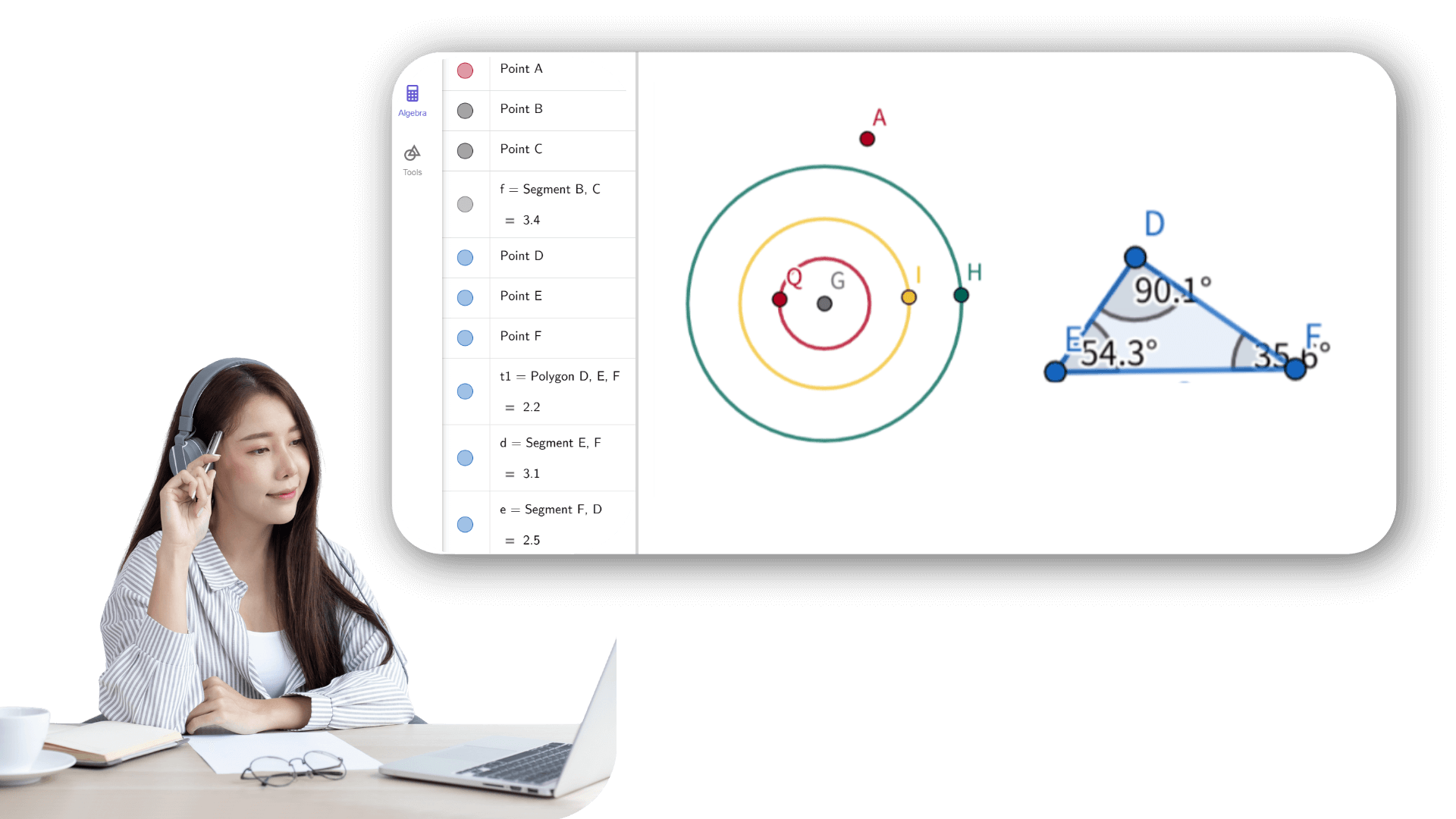
2. ![]() Construa um círculo com centro em B passando por A,
selecionando ambos os pontos nesta ordem.
Construa um círculo com centro em B passando por A,
selecionando ambos os pontos nesta ordem.
3. ![]() Arraste os pontos A e B para verificar se o círculo está
conectado a eles.
Arraste os pontos A e B para verificar se o círculo está
conectado a eles.
4. ![]() Construa um círculo com centro em B passando por A,
selecionando ambos os pontos nesta ordem.
Construa um círculo com centro em B passando por A,
selecionando ambos os pontos nesta ordem.
5. ![]() Interseccione ambos os círculos selecionando-os para obter
o ponto C.
Interseccione ambos os círculos selecionando-os para obter
o ponto C.
6. ![]() Crie o polígono ABC no sentido anti-horário. Para fechar o
polígono, selecione novamente o primeiro ponto.
Crie o polígono ABC no sentido anti-horário. Para fechar o
polígono, selecione novamente o primeiro ponto.
7. ![]() Oculte os dois círculos ativando a ferramenta
Mostrar/Ocultar Objeto e selecionando-os. Confirme sua
seleção escolhendo a ferramenta Mover.
Oculte os dois círculos ativando a ferramenta
Mostrar/Ocultar Objeto e selecionando-os. Confirme sua
seleção escolhendo a ferramenta Mover.
8. ![]() Mostre os ângulos internos do triângulo clicando dentro do
triângulo.
Mostre os ângulos internos do triângulo clicando dentro do
triângulo.
Dica: Se você obtiver os ângulos externos do
triângulo, provavelmente criou o polígono no sentido
horário.
9. ![]() Aplique o Teste de Arraste para verificar se a construção
está correta.
Aplique o Teste de Arraste para verificar se a construção
está correta.
1. ![]() Crie um triângulo arbitrário ABC clicando três vezes na
Visualização Gráfica e depois selecionando novamente o
primeiro ponto criado.
Crie um triângulo arbitrário ABC clicando três vezes na
Visualização Gráfica e depois selecionando novamente o
primeiro ponto criado.
2. ![]() Construa a mediatriz de cada lado do triângulo.
Construa a mediatriz de cada lado do triângulo.
Dica:
A ferramenta Mediatriz pode ser aplicada a um segmento
existente.
3. ![]() Crie o ponto de interseção D de duas das mediatrizes.
Crie o ponto de interseção D de duas das mediatrizes.
Dica:
A ferramenta Interseção pode ser aplicada à interseção de
três retas ou selecionando sucessivamente duas das três
mediatrizes.
4. ![]() Construa um círculo com centro em D passando por um dos
vértices do triângulo ABC, primeiro selecionando D e depois
um dos vértices do triângulo.
Construa um círculo com centro em D passando por um dos
vértices do triângulo ABC, primeiro selecionando D e depois
um dos vértices do triângulo.
5. ![]() Realize o Teste de Arraste movendo os vértices do triângulo
para verificar se sua construção está correta.
Realize o Teste de Arraste movendo os vértices do triângulo
para verificar se sua construção está correta.
1. ![]() Certifique-se de que você tem a imagem da flor amarela
salva em seu computador antes de iniciar a construção.
Certifique-se de que você tem a imagem da flor amarela
salva em seu computador antes de iniciar a construção.
2. ![]() Crie um novo ponto A.
Crie um novo ponto A.
3. ![]() Construa uma reta de reflexão através de dois novos pontos
clicando duas vezes na Visualização Gráfica.
Construa uma reta de reflexão através de dois novos pontos
clicando duas vezes na Visualização Gráfica.
4. ![]() Espelhe o ponto A na reta para obter sua imagem A’.
Espelhe o ponto A na reta para obter sua imagem A’.
Dica:
Primeiro selecione o ponto A e depois a reta.
5. ![]() Crie um segmento entre o ponto A e sua imagem A’
selecionando ambos os pontos.
Crie um segmento entre o ponto A e sua imagem A’
selecionando ambos os pontos.
6. ![]() Ative o rastro para os pontos A e A′.
Ative o rastro para os pontos A e A′.
Dica:
Clique com o botão direito (MacOS: Ctrl-clique) em um ponto
e selecione Mostrar Rastro.
Nota: Sempre que o
ponto A for movido, ele deixará um rastro na Visualização
Gráfica.
7. ![]() Arraste o ponto A para desenhar um rastro.
Arraste o ponto A para desenhar um rastro.
Dica:
O item de menu Atualizar Visualizações no Menu Visualização
limpa todos os rastros.
1. ![]() Certifique-se de que você tem a imagem do pôr do sol salva
em seu computador antes de iniciar a construção.
Certifique-se de que você tem a imagem do pôr do sol salva
em seu computador antes de iniciar a construção.
2. ![]() Insira a imagem do pôr do sol na parte esquerda da
Visualização Gráfica usando a ferramenta Imagem.
Insira a imagem do pôr do sol na parte esquerda da
Visualização Gráfica usando a ferramenta Imagem.
Nota: O primeiro ponto de canto A e o segundo ponto
de canto B da imagem são criados automaticamente.
3. ![]() Mova o ponto A no canto inferior esquerdo da imagem e
observe como isso afeta a imagem.
Mova o ponto A no canto inferior esquerdo da imagem e
observe como isso afeta a imagem.
4. ![]() Exclua o ponto B usando a ferramenta Excluir.
Exclua o ponto B usando a ferramenta Excluir.
5. ![]() Crie um novo ponto B digitando B = A + (3, 0) na Barra de
Entrada.
Crie um novo ponto B digitando B = A + (3, 0) na Barra de
Entrada.
Dica: Não se esqueça de pressionar
Enter após digitar.
6. ![]() Defina o novo ponto B como o SEGUNDO ponto de canto da
imagem para alterar sua largura para 3 cm.
Defina o novo ponto B como o SEGUNDO ponto de canto da
imagem para alterar sua largura para 3 cm.
Dica: Abra as Configurações da imagem e selecione a
aba Posição.
7. ![]() Crie uma reta vertical através de dois pontos no meio da
Visualização Gráfica usando a ferramenta Reta.
Crie uma reta vertical através de dois pontos no meio da
Visualização Gráfica usando a ferramenta Reta.
8. ![]() Espelhe a imagem na reta usando a ferramenta Refletir sobre
a Reta, selecionando a imagem e depois a reta.
Espelhe a imagem na reta usando a ferramenta Refletir sobre
a Reta, selecionando a imagem e depois a reta.
9. ![]() Você pode querer reduzir a opacidade da imagem para
distingui-la melhor da original (Configurações da imagem,
aba Cor).
Você pode querer reduzir a opacidade da imagem para
distingui-la melhor da original (Configurações da imagem,
aba Cor).
1. ![]() Certifique-se de que você tem a imagem do Bart Simpson
salva em seu computador antes de iniciar a construção.
Certifique-se de que você tem a imagem do Bart Simpson
salva em seu computador antes de iniciar a construção.
2. ![]() Selecione a ferramenta Imagem para inserir a imagem do
Bart.
Selecione a ferramenta Imagem para inserir a imagem do
Bart.
Dica: A Calculadora de Geometria criará
automaticamente o primeiro e o segundo ponto de canto A e B
da imagem.
3. ![]() Arraste o primeiro ponto de canto A da imagem para a
posição (1, 1).
Arraste o primeiro ponto de canto A da imagem para a
posição (1, 1).
4. ![]() Crie o ponto D = (1, 3.9).
Crie o ponto D = (1, 3.9).
Dica: Você pode
digitar as coordenadas diretamente na Barra de
Entrada.
5. ![]() Defina o ponto D como o QUARTO ponto de canto da imagem.
Defina o ponto D como o QUARTO ponto de canto da imagem.
Dica:
Abra as Configurações da imagem e selecione a aba
Posição.
6. ![]() Crie um triângulo rígido ABD usando a ferramenta Polígono
Rígido.
Crie um triângulo rígido ABD usando a ferramenta Polígono
Rígido.
Dica: Feche o polígono selecionando
novamente o primeiro ponto. O polígono resultante manterá
sua forma ao ser movido. Ele pode ser movido ou rotacionado
arrastando dois vértices.
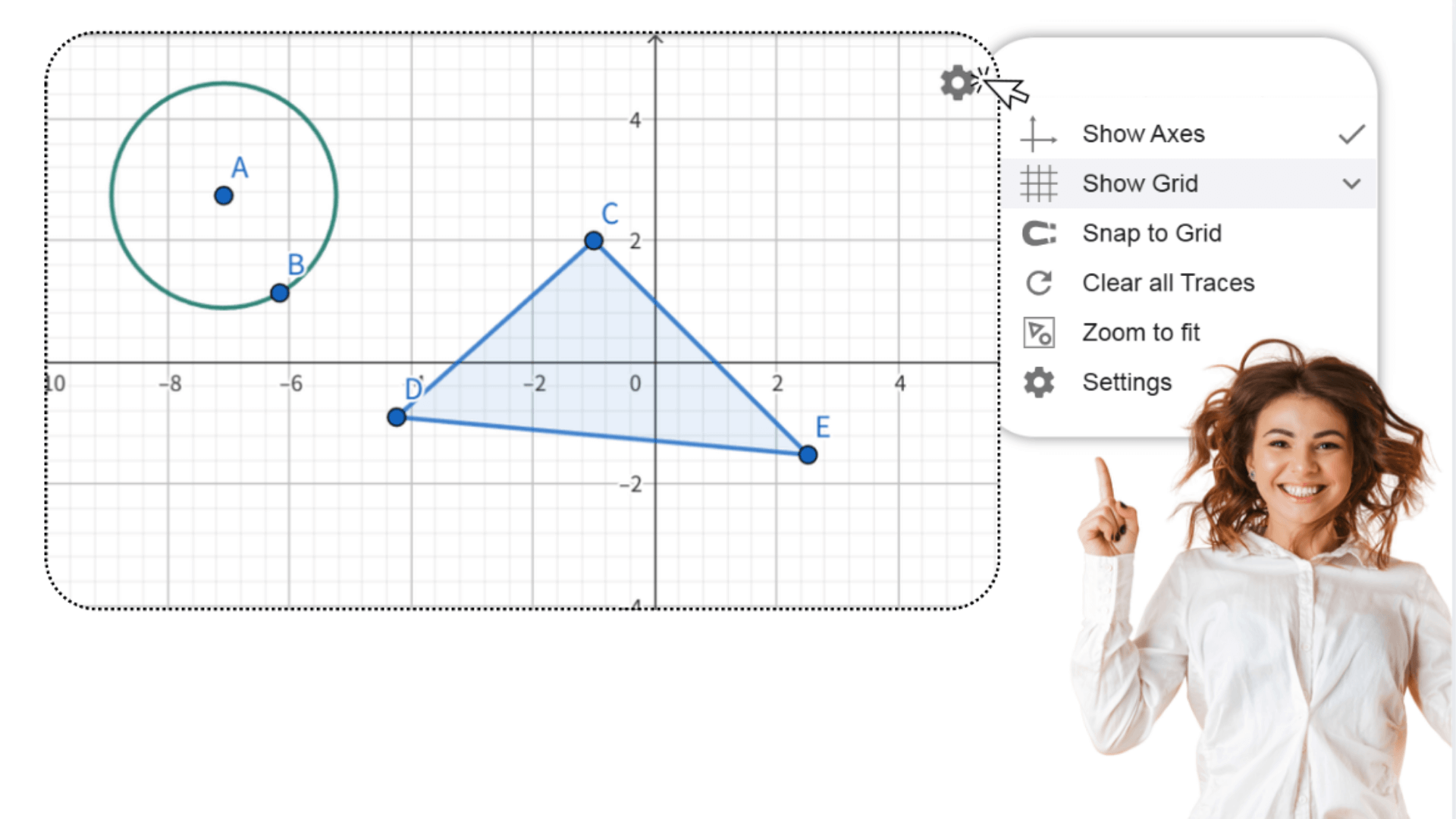
1. ![]() Crie um triângulo arbitrário ABC no primeiro quadrante,
posicionando os vértices nos pontos da grade.
Crie um triângulo arbitrário ABC no primeiro quadrante,
posicionando os vértices nos pontos da grade.
2. ![]() Crie um novo ponto D na origem do sistema de
coordenadas.
Crie um novo ponto D na origem do sistema de
coordenadas.
3. ![]() Renomeie o ponto D para O.
Renomeie o ponto D para O.
Dica: Selecione o
ponto D e apenas digite O para abrir o diálogo de
renomeação.
4. ![]() Crie um deslizante para o ângulo α.
Crie um deslizante para o ângulo α.
Dica: Na
janela de diálogo do Deslizante, marque Ângulo e defina o
incremento para 90°. Certifique-se de não apagar o símbolo
°.
5. ![]() Use a ferramenta Rotacionar em torno de Ponto para
rotacionar o triângulo ABC em torno do ponto O pelo ângulo
α.
Use a ferramenta Rotacionar em torno de Ponto para
rotacionar o triângulo ABC em torno do ponto O pelo ângulo
α.
Dicas: Ative a ferramenta e selecione o
triângulo antes de selecionar o centro de rotação. No
diálogo que aparece, insira α como o ângulo usando o Teclado
Virtual e escolha rotação no sentido anti-horário.
6. ![]() Crie os segmentos AO e A’O.
Crie os segmentos AO e A’O.
7. ![]() Crie o ângulo AOA’.
Crie o ângulo AOA’.
Dica: Selecione os pontos
no sentido anti-horário.
8. ![]() Oculte o rótulo do ângulo AOA’.
Oculte o rótulo do ângulo AOA’.
9. ![]() Mova o deslizante e explore a imagem do triângulo.
Mova o deslizante e explore a imagem do triângulo.
1. ![]() Crie deslizantes a, b e c para os comprimentos dos lados do
triângulo com intervalo de 0 a 10 e incremento de 0,5
cada.
Crie deslizantes a, b e c para os comprimentos dos lados do
triângulo com intervalo de 0 a 10 e incremento de 0,5
cada.
2. ![]() Defina os valores dos deslizantes para a = 8, b = 6,5 e c =
10.
Defina os valores dos deslizantes para a = 8, b = 6,5 e c =
10.
3. ![]() Crie o segmento f com comprimento c.
Crie o segmento f com comprimento c.
Dica: Os
pontos A e B são as extremidades do segmento.
4. ![]() Crie um círculo d com centro em A e raio b.
Crie um círculo d com centro em A e raio b.
5. ![]() Crie um círculo e com centro em B e raio a.
Crie um círculo e com centro em B e raio a.
6. ![]() Construa o ponto de interseção C dos dois círculos e e
f.
Construa o ponto de interseção C dos dois círculos e e
f.
7. ![]() Crie o triângulo ABC.
Crie o triângulo ABC.
8. ![]() Crie os ângulos internos α, β e γ do triângulo ABC.
Crie os ângulos internos α, β e γ do triângulo ABC.
9. ![]() Crie um ponto D no círculo d.
Crie um ponto D no círculo d.
10. ![]() Crie o segmento g entre os pontos A e D.
Crie o segmento g entre os pontos A e D.
11. ![]() Construa o ponto médio E do segmento g.
Construa o ponto médio E do segmento g.
12. ![]() Insira o texto1: b e anexe ao ponto E.
Insira o texto1: b e anexe ao ponto E.
Dica:
Após selecionar a ferramenta Texto, clique no ponto E. Abra
Avançado e selecione b na aba Objetos.
13. ![]() Crie um ponto F no círculo e.
Crie um ponto F no círculo e.
14. ![]() Crie o segmento h entre os pontos B e F.
Crie o segmento h entre os pontos B e F.
15. ![]() Construa o ponto médio G do segmento h.
Construa o ponto médio G do segmento h.
16. ![]() Insira o texto2: a e anexe ao ponto G.
Insira o texto2: a e anexe ao ponto G.
17. ![]() Oculte os pontos D, E, F e G usando a ferramenta
Mostrar/Ocultar Objeto.
Oculte os pontos D, E, F e G usando a ferramenta
Mostrar/Ocultar Objeto.
18. ![]() Aprimore sua construção usando a Barra de Estilo e combine
as cores dos objetos correspondentes.
Aprimore sua construção usando a Barra de Estilo e combine
as cores dos objetos correspondentes.
1. ![]() Crie um triângulo ABC com orientação anti-horária.
Crie um triângulo ABC com orientação anti-horária.
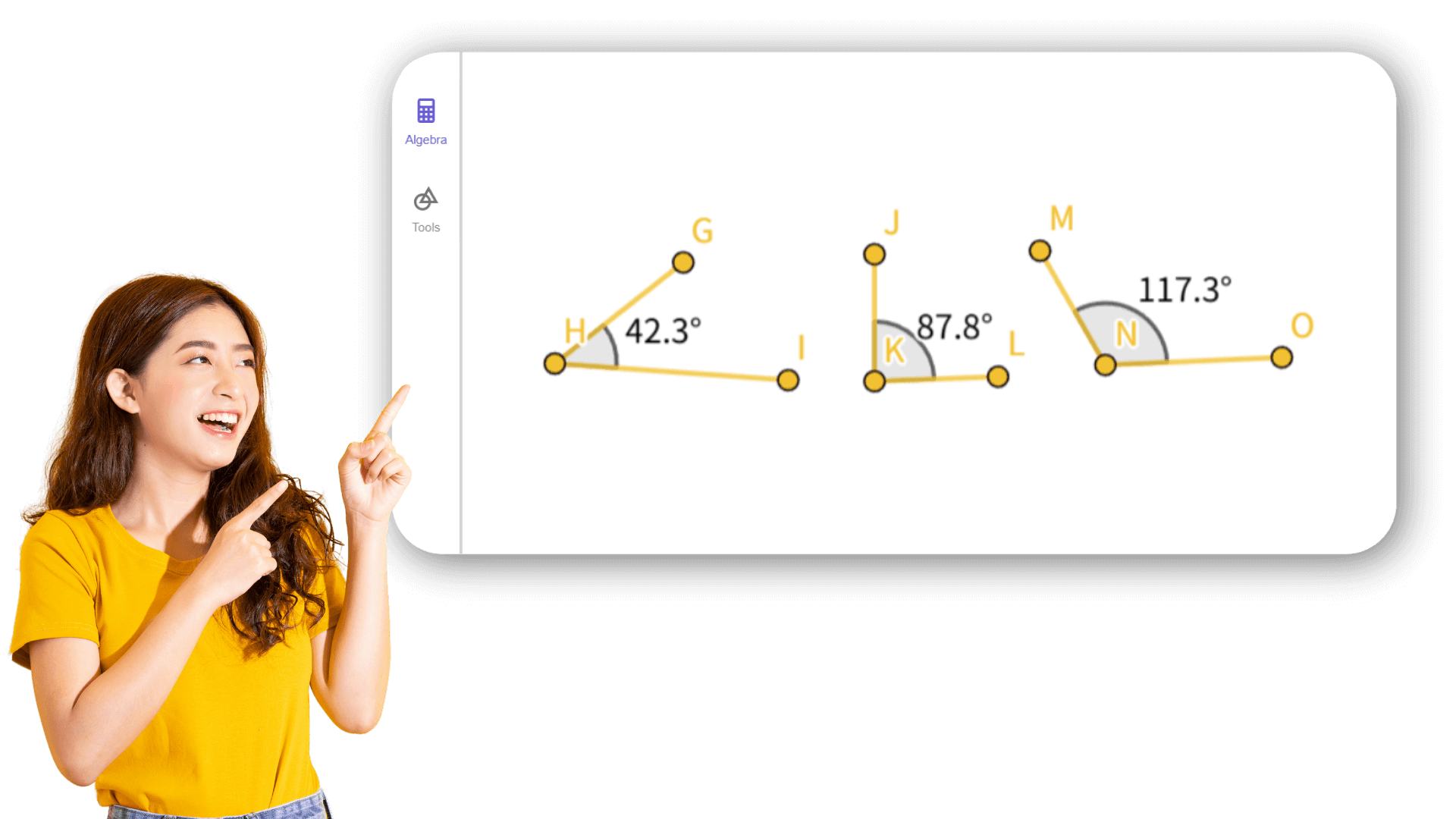
2. ![]() Crie os ângulos α, β e γ do triângulo ABC.
Crie os ângulos α, β e γ do triângulo ABC.
3. ![]() Crie um deslizante para o ângulo δ com intervalo de 0° a
180° e incremento de 10°.
Crie um deslizante para o ângulo δ com intervalo de 0° a
180° e incremento de 10°.
4. ![]() Crie um deslizante para o ângulo ε com intervalo de 0° a
180° e incremento de 10°.
Crie um deslizante para o ângulo ε com intervalo de 0° a
180° e incremento de 10°.
5. ![]() Crie o ponto médio D do segmento AC e o ponto médio E do
segmento AB.
Crie o ponto médio D do segmento AC e o ponto médio E do
segmento AB.
6. ![]() Gire o triângulo em torno do ponto D pelo ângulo δ (sentido
horário).
Gire o triângulo em torno do ponto D pelo ângulo δ (sentido
horário).
Dica: Insira δ usando o Teclado
Virtual.
7. ![]() Gire o triângulo em torno do ponto E pelo ângulo ε (sentido
anti-horário).
Gire o triângulo em torno do ponto E pelo ângulo ε (sentido
anti-horário).
Dica: Insira ε usando o Teclado
Virtual.
8. ![]() Mova ambos os deslizantes δ e ε para mostrar 180°.
Mova ambos os deslizantes δ e ε para mostrar 180°.
9. ![]() Crie o ângulo ζ usando os pontos A’C’B’.
Crie o ângulo ζ usando os pontos A’C’B’.
Dica:
Para garantir que selecionou os vértices corretos, altere o
ângulo δ ou use o comando
angle(A’, C’, B’).
10. ![]() Crie o ângulo η usando os pontos C'1B'1A'1.
Crie o ângulo η usando os pontos C'1B'1A'1.
Dica:
Para garantir que selecionou os vértices corretos, altere o
ângulo ε antes ou use o comando
angle(C'1, B'1, A'1).
11. ![]() Aprimore sua construção usando a Barra de Estilo.
Aprimore sua construção usando a Barra de Estilo.
Dica:
Ângulos congruentes devem ter a mesma cor.
12. ![]() Crie um texto dinâmico exibindo os ângulos internos e seus
valores (ex: digite α = e selecione α na lista de objetos na
aba Avançado).
Crie um texto dinâmico exibindo os ângulos internos e seus
valores (ex: digite α = e selecione α na lista de objetos na
aba Avançado).
13. ![]() Calcule a soma dos ângulos digitando
Calcule a soma dos ângulos digitando
soma = α + β + γ na Barra de Entrada.
14. ![]() Insira a soma dos ângulos como texto dinâmico:
Insira a soma dos ângulos como texto dinâmico:
α + β + γ = e selecione soma na lista de
objetos da aba.
15. ![]() Combine as cores dos ângulos e textos correspondentes
usando a Barra de Estilo.
Combine as cores dos ângulos e textos correspondentes
usando a Barra de Estilo.
16. ![]() Fixe todos os textos que não devem ser movidos usando a
Barra de Estilo.
Fixe todos os textos que não devem ser movidos usando a
Barra de Estilo.
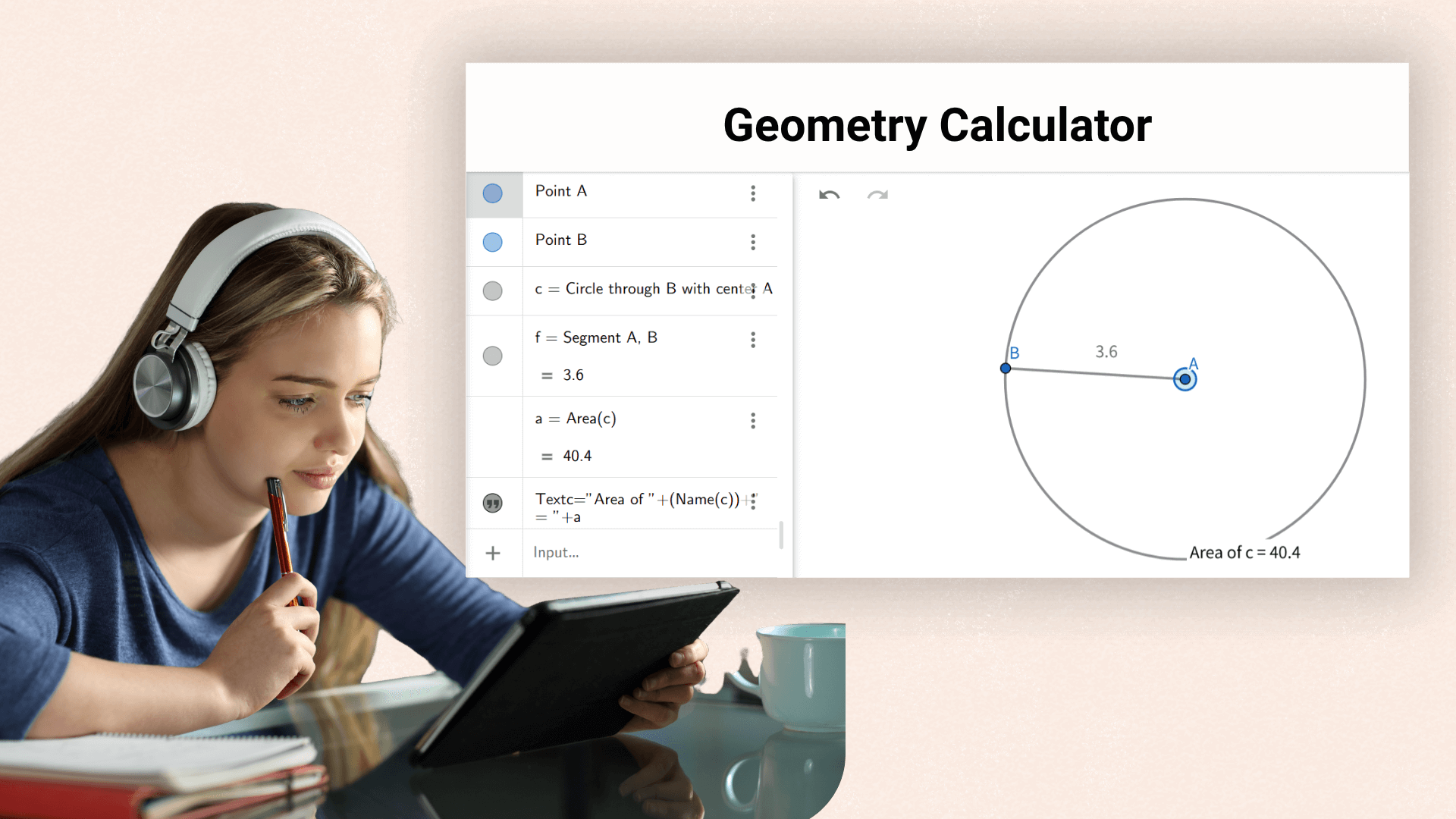
Ajuda os estudantes a verificar rapidamente fórmulas e resolver problemas durante as aulas de geometria, melhorando a eficiência do aprendizado.
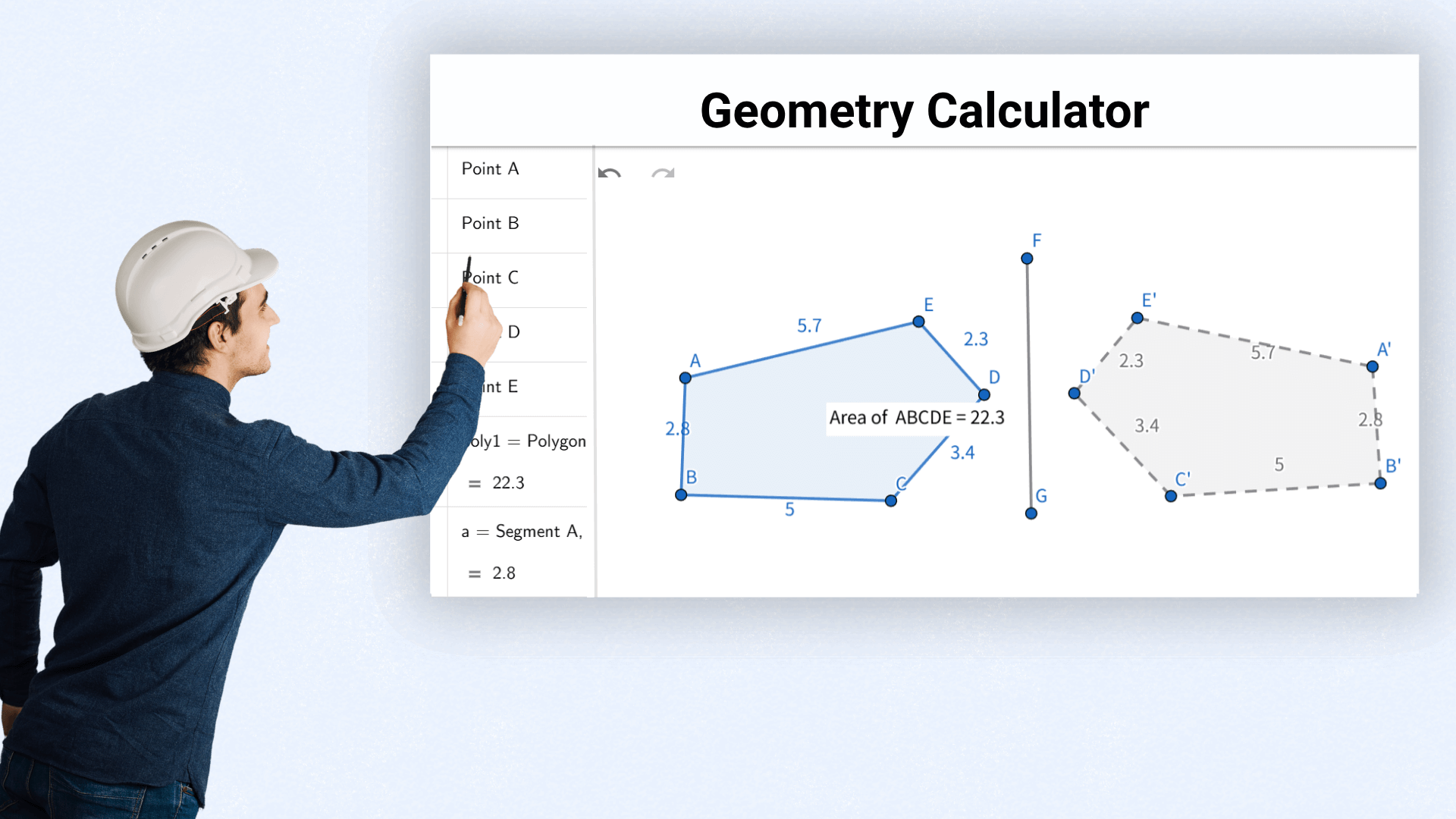
Arquitetos calculam área e volume para avaliar a viabilidade do projeto e otimizar o layout espacial.

Entusiastas usam a calculadora de geometria para medir materiais com precisão ao criar projetos de artesanato geométrico.
Explore a conexão entre álgebra e geometria, aprofunde a compreensão dos conceitos matemáticos e use a calculadora de geometria para concluir tarefas e projetos.
Professores usam a calculadora de geometria para apresentar visualmente conceitos geométricos durante o planejamento de aulas e demonstrações em sala, melhorando a eficácia do ensino.
Engenheiros confiam na calculadora de geometria para calcular com precisão ângulos e comprimentos em projetos estruturais ou mecânicos, reduzindo erros de cálculos manuais.

Hobbyistas usam a calculadora para garantir medições precisas ao criar artesanatos baseados em geometria.
Use a calculadora de geometria para esboçar e ajustar rapidamente conceitos iniciais de design, obtendo uma compreensão clara das relações espaciais antes de passar para ferramentas CAD detalhadas.

Pesquisadores visualizam estruturas complexas e analisam dados usando os recursos de desenho e cálculo da calculadora, apoiando a exploração científica.
Utiliza algoritmos avançados para garantir resultados geométricos de alta precisão.
Interface simples e intuitiva com fluxo de trabalho claro—não é necessário treinamento complexo, mesmo para novos usuários.
Integra várias ferramentas e recursos para atender a diversas necessidades de cálculo geométrico em um só lugar.
Desempenho rápido e operação suave, mesmo com grande volume de dados ou fórmulas complexas.
Desenhe formas com precisão, controlando tamanho e propriedades, fornecendo uma base visual confiável para análise e pesquisa.
Todos os recursos da calculadora de geometria online estão disponíveis sem custo, tornando ferramentas geométricas de alta qualidade acessíveis a todos.
Sim, é totalmente gratuita. Os usuários podem acessar todos os recursos sem nenhum custo.
Abra nosso site, selecione “Nova Geometria” e depois clique em ferramentas como “Ponto”, “Segmento” ou “Círculo” para posicionar formas na área de desenho.
É amplamente utilizada no ensino de matemática e pode também auxiliar no ensino de geometria, álgebra e cálculo.
Desenhe ou importe a forma, selecione o objeto que deseja medir e escolha propriedades como distância, comprimento, ângulo, perímetro ou área. Os resultados aparecerão na área de desenho ou álgebra.
Sim. A calculadora de geometria é fácil de usar, com uma interface intuitiva—perfeita para iniciantes começarem rapidamente.
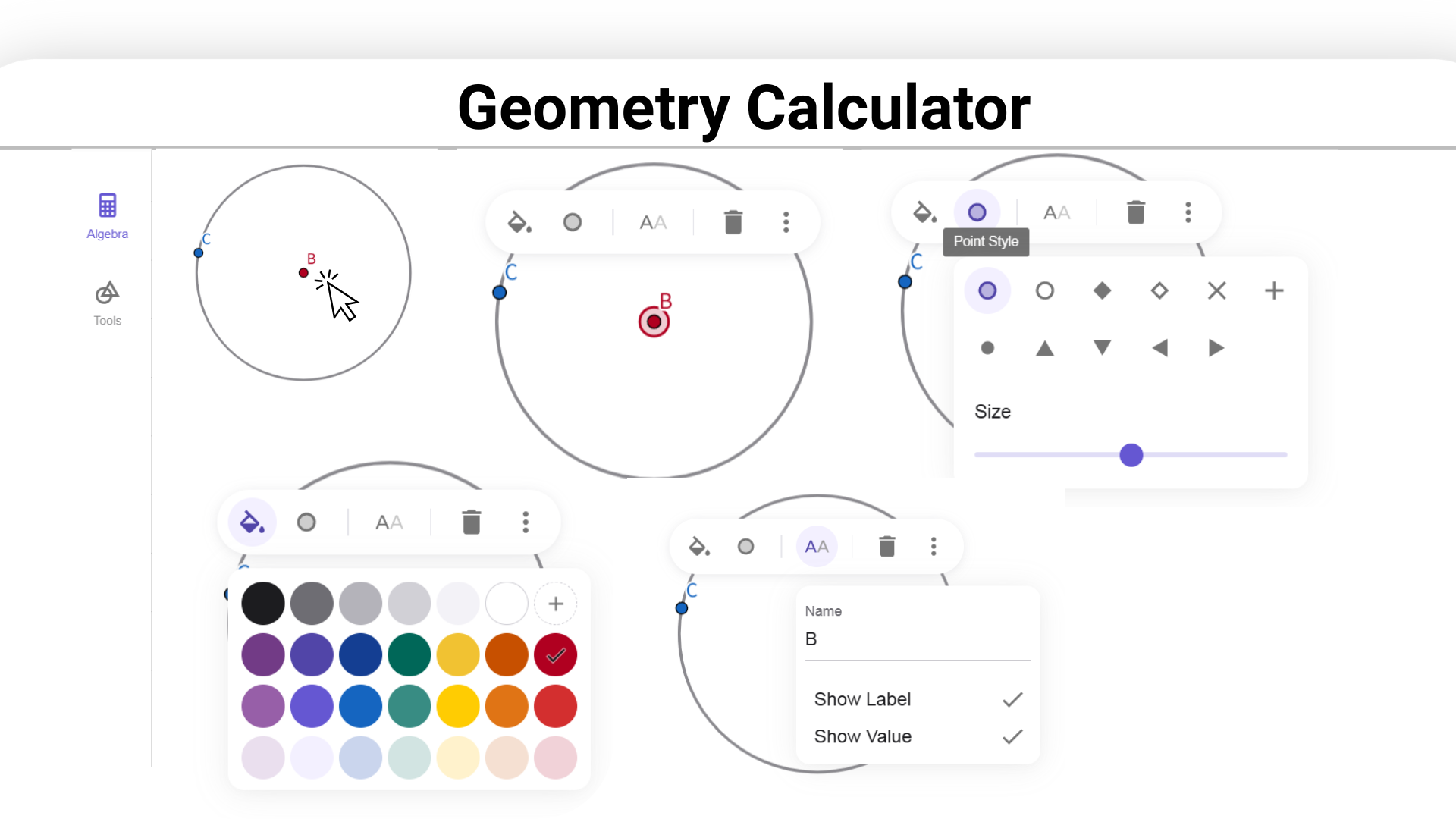
Selecione a forma e use o menu do botão direito ou o painel de propriedades para editar sua aparência, incluindo cor, estilo de linha e preenchimento.
Nossa calculadora de geometria utiliza algoritmos avançados para fornecer resultados precisos e confiáveis.
Ajuda os estudantes a explorar a ligação entre álgebra e geometria, apoiando-os na conclusão de tarefas e projetos de pesquisa de forma mais eficiente.