Estudantes
A Calculadora Gráfica beneficia estudantes desde o ensino fundamental até o universitário. Ela ajuda a compreender conceitos matemáticos e cultiva habilidades de resolução de problemas.
Uma calculadora de graficación pode resolver equações e desenhar gráficos de funções, ajudando você a compreender intuitiva e precisamente os padrões cambiantes das funções.
A Calculadora Gráfica é uma ferramenta de desenho poderosa e tecnologicamente avançada que nos ajuda a traçar gráficos de funções, realizar cálculos complexos e conduzir análises de dados. Ajustando parâmetros para afetar a transformação de gráficos, a aprendizagem matemática e a pesquisa se tornam mais intuitivas, eficientes e interessantes.
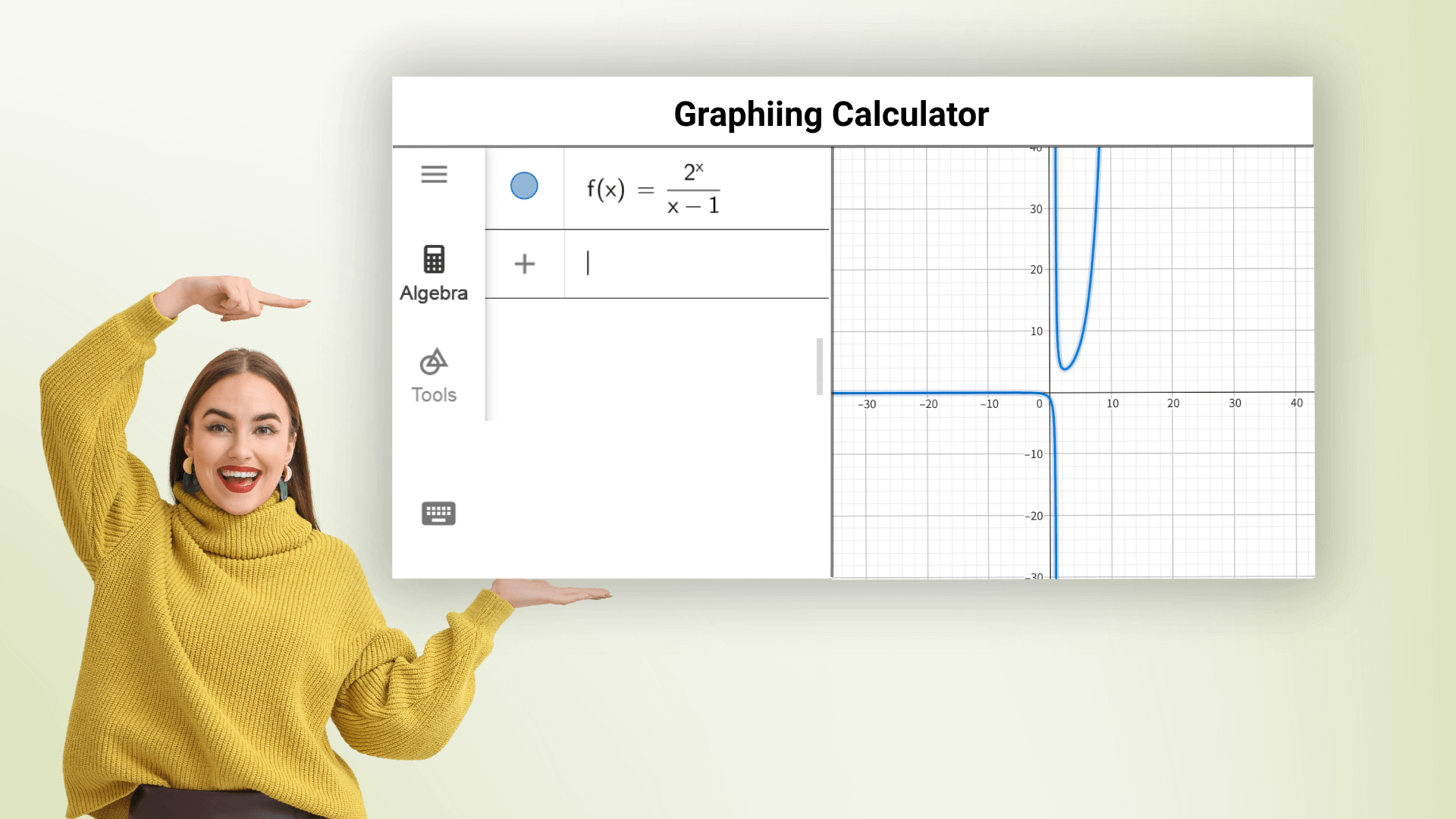
A Calculadora Gráfica pode traçar vários gráficos de funções, incluindo funções lineares, parabólicas, trigonométricas e logarítmicas, e pode traçar múltiplas equações de uma vez em cores diferentes. Basta inserir a expressão da função para obter rapidamente um gráfico preciso e observar as tendências e características da função. A calculadora gráfica online ajuda a todos a dominar a matemática e evitar cálculos complexos.
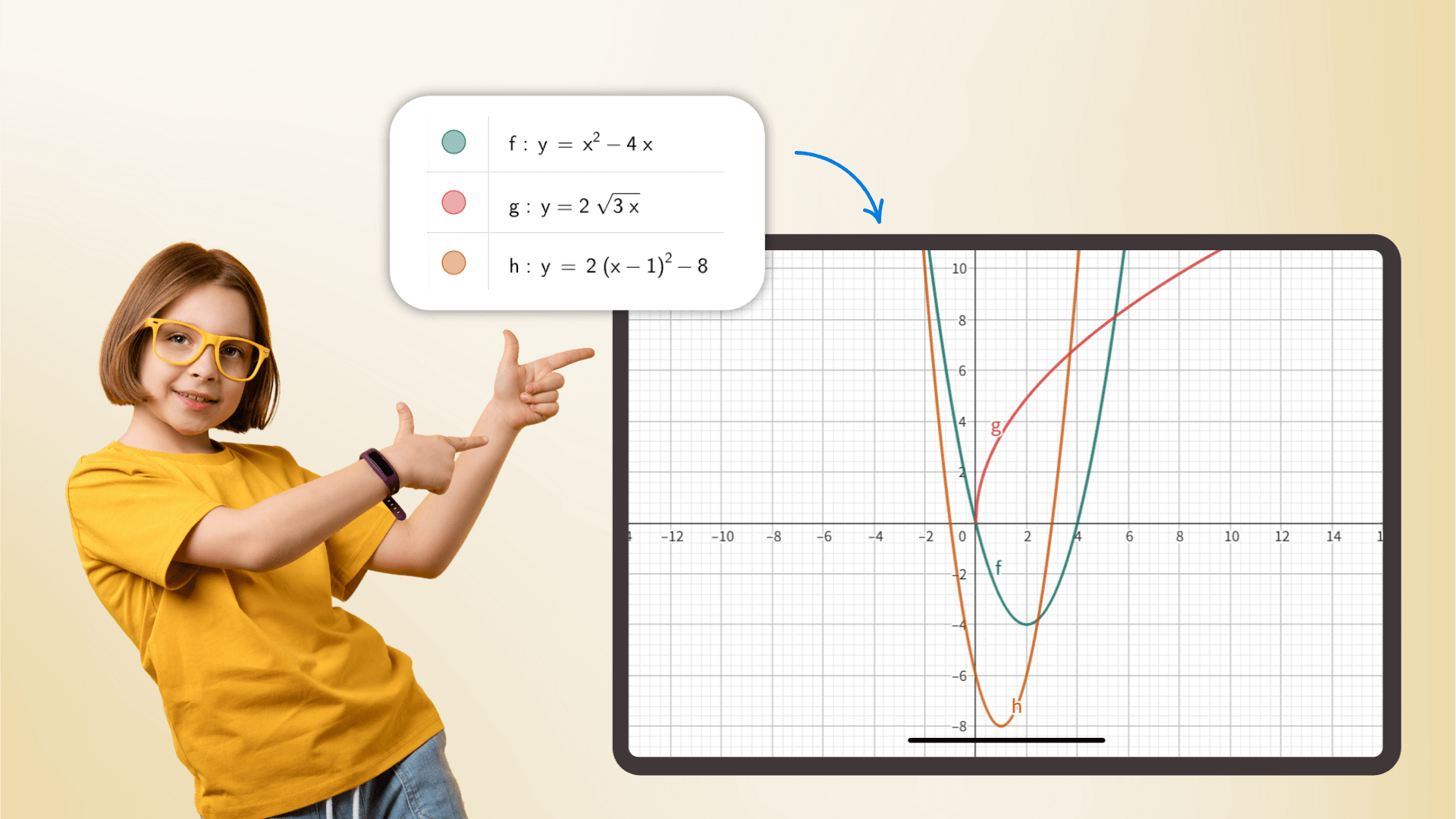
Como uma calculadora científica, ela lida com tudo, desde aritmética básica até matemática avançada, cálculo, estatísticas de probabilidade e muito mais. Com cálculos orientados por precisão, ela serve como uma assistente indispensável para estudantes e pesquisadores, elevando a eficiência em contextos acadêmicos e profissionais.
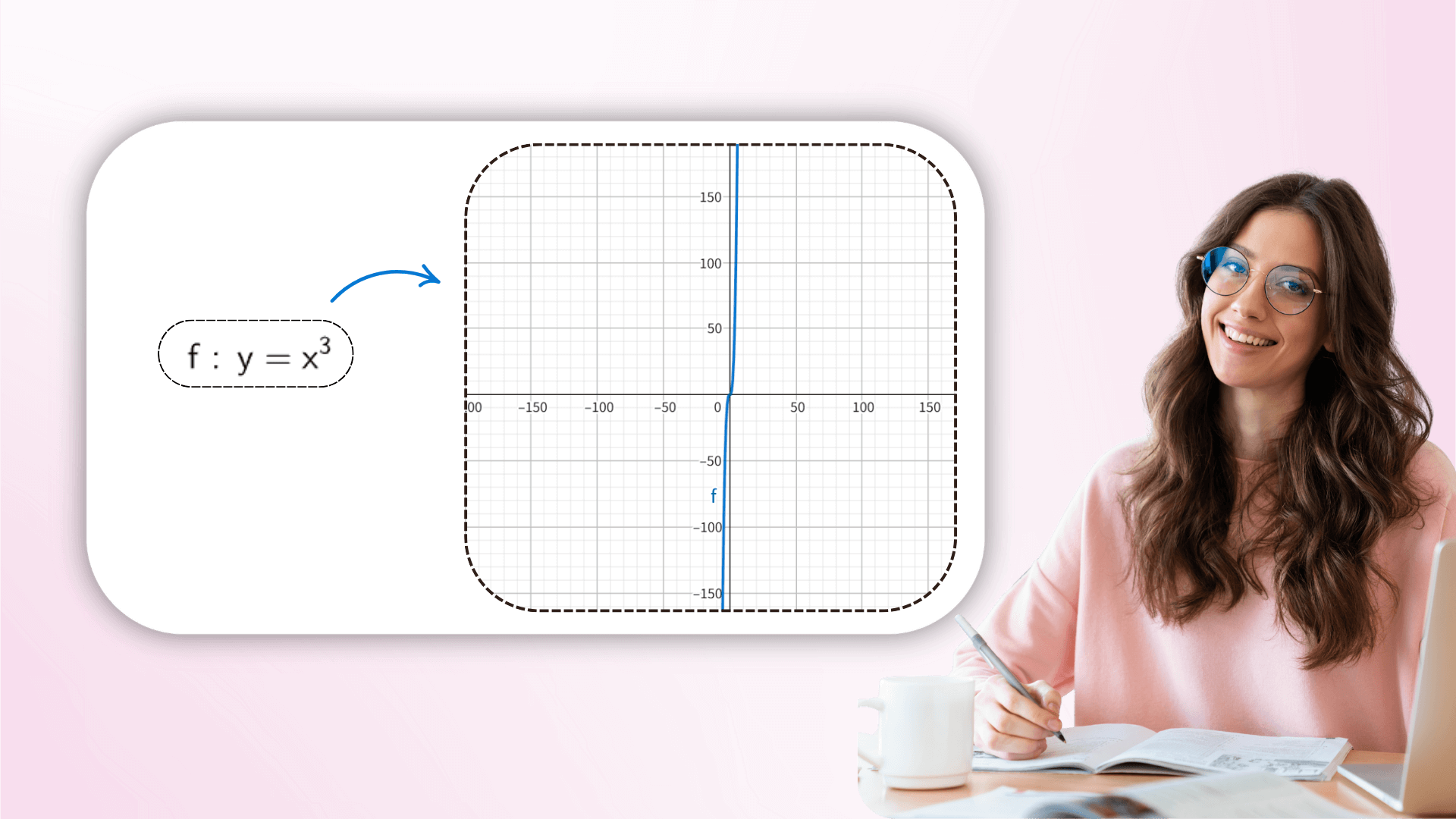
Ajustando os valores dos parâmetros em tempo real, os usuários podem observar a transformação dinâmica da imagem para entender como os coeficientes afetam a geometria da função, desde a tradução linear até as transformações complexas, ligando fórmulas abstratas à visão. Essa exploração interativa pode aprofundar a compreensão das equações matemáticas.
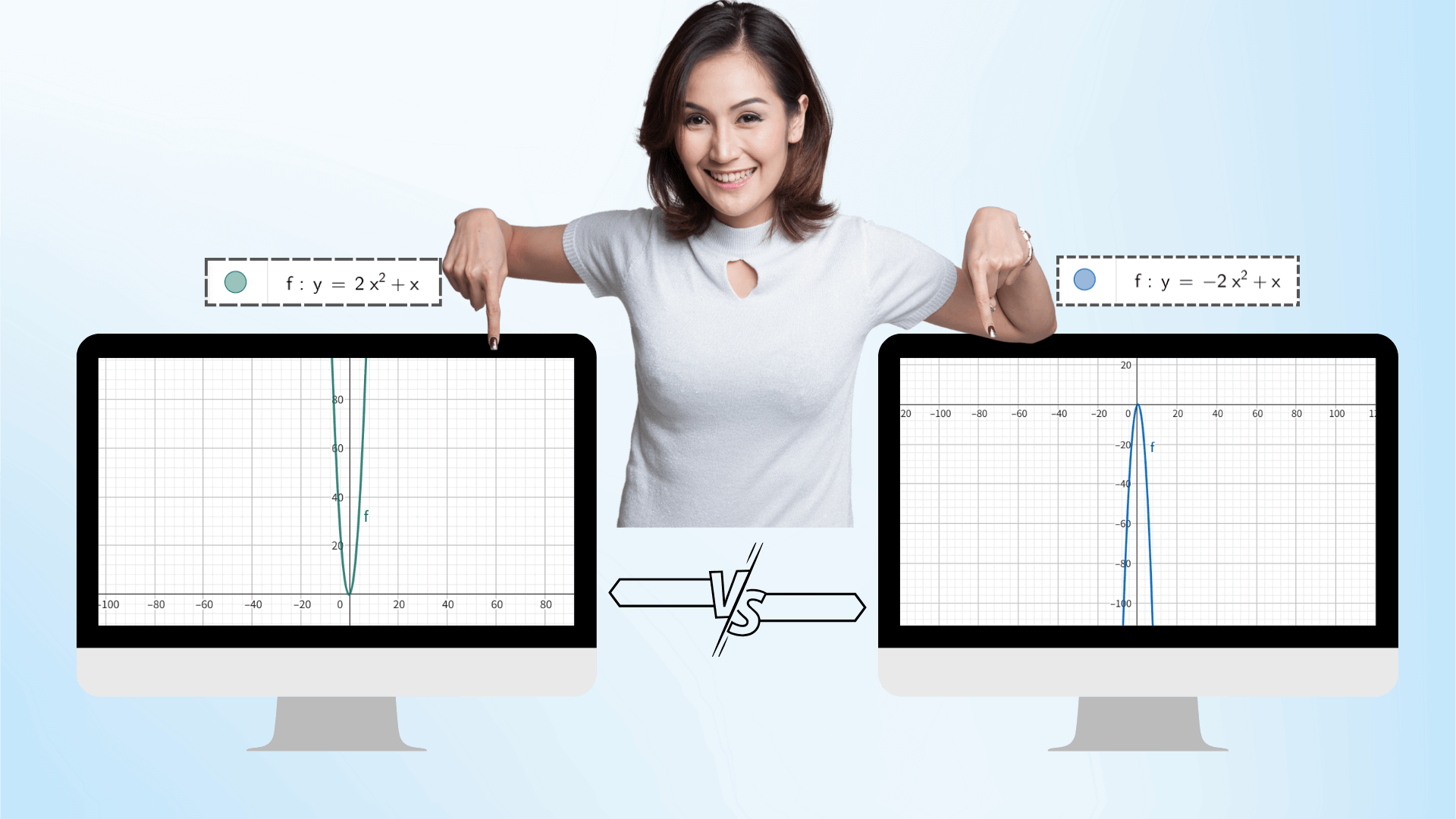
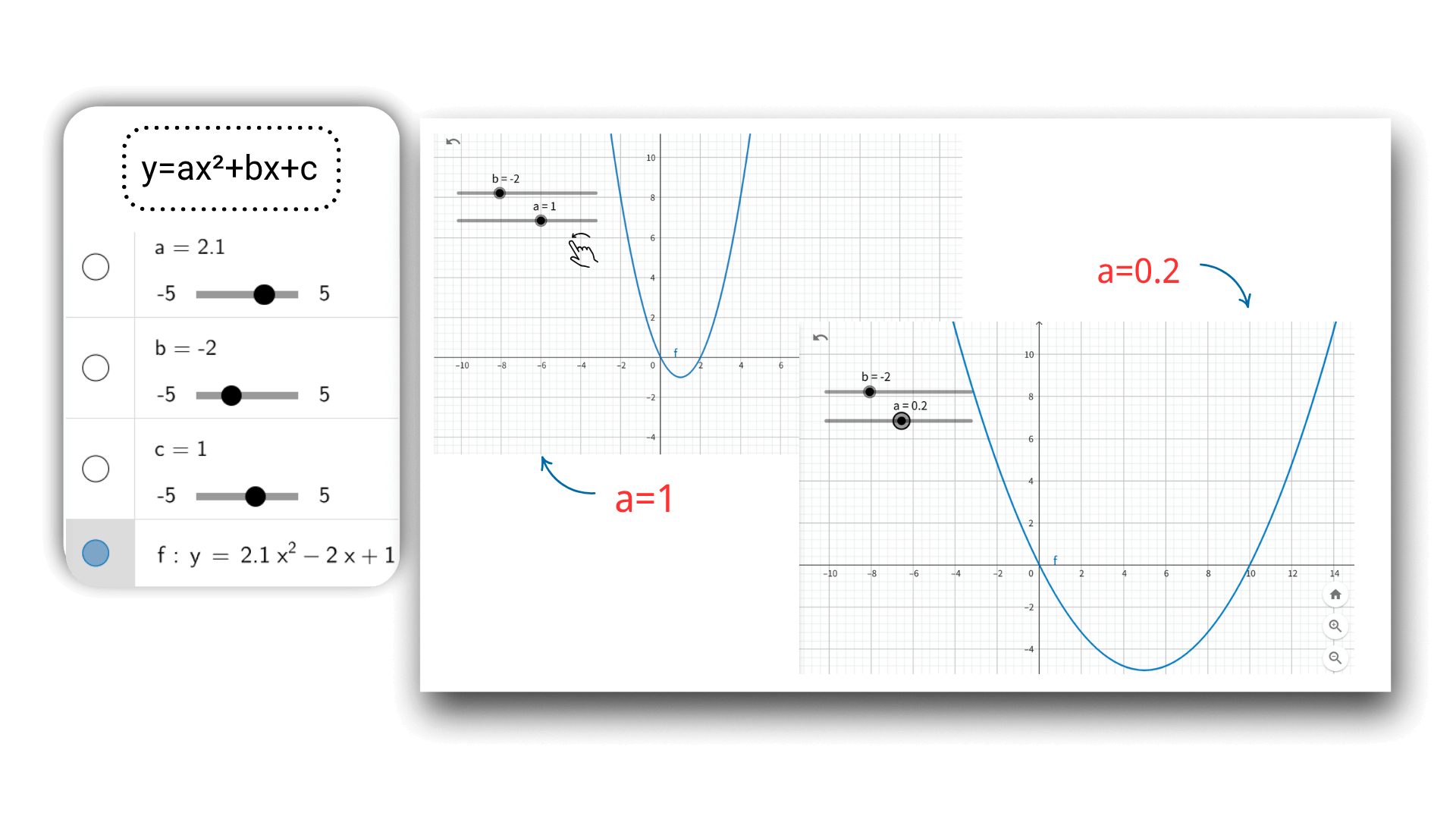
Usando a tecnologia de gráficos de IA, após inserir a função, você pode ajustar dinamicamente os parâmetros através do controle deslizante, como a, b, c de uma função quadrática. A imagem se deformará em tempo real como uma animação, e os dados de coordenadas serão atualizados sincronamente, revelando intuitivamente o impacto das mudanças de parâmetros na imagem, e melhorando a compreensão da conexão entre os conceitos matemáticos.
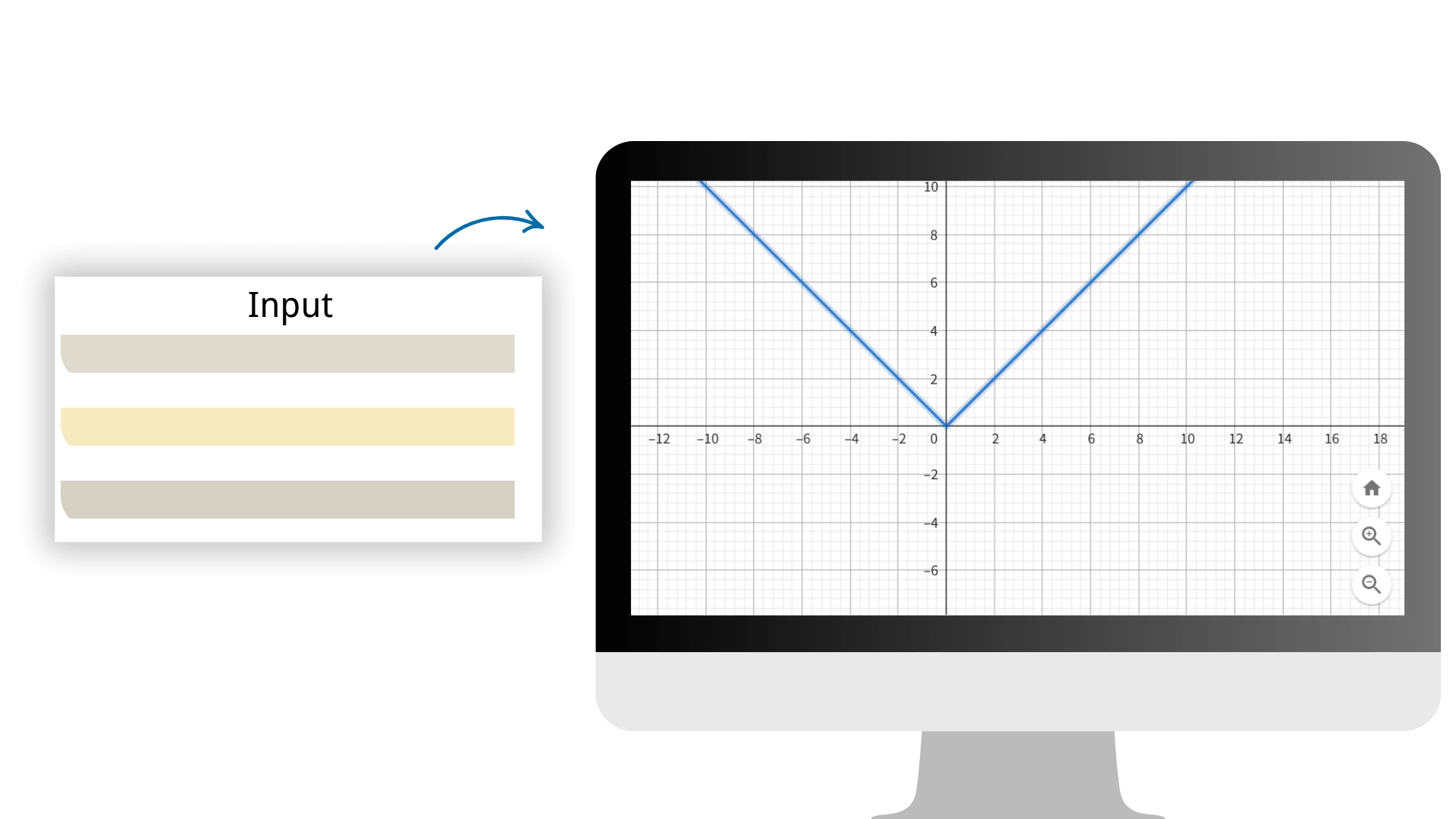
Adotando algoritmos avançados de cálculo, garantimos que cada resultado de cálculo tenha uma precisão extremamente alta, fornecendo suporte de dados confiável para o seu trabalho matemático. Basta inserir a matriz em nossa calculadora de imagens para gerar várias imagens com um clique.
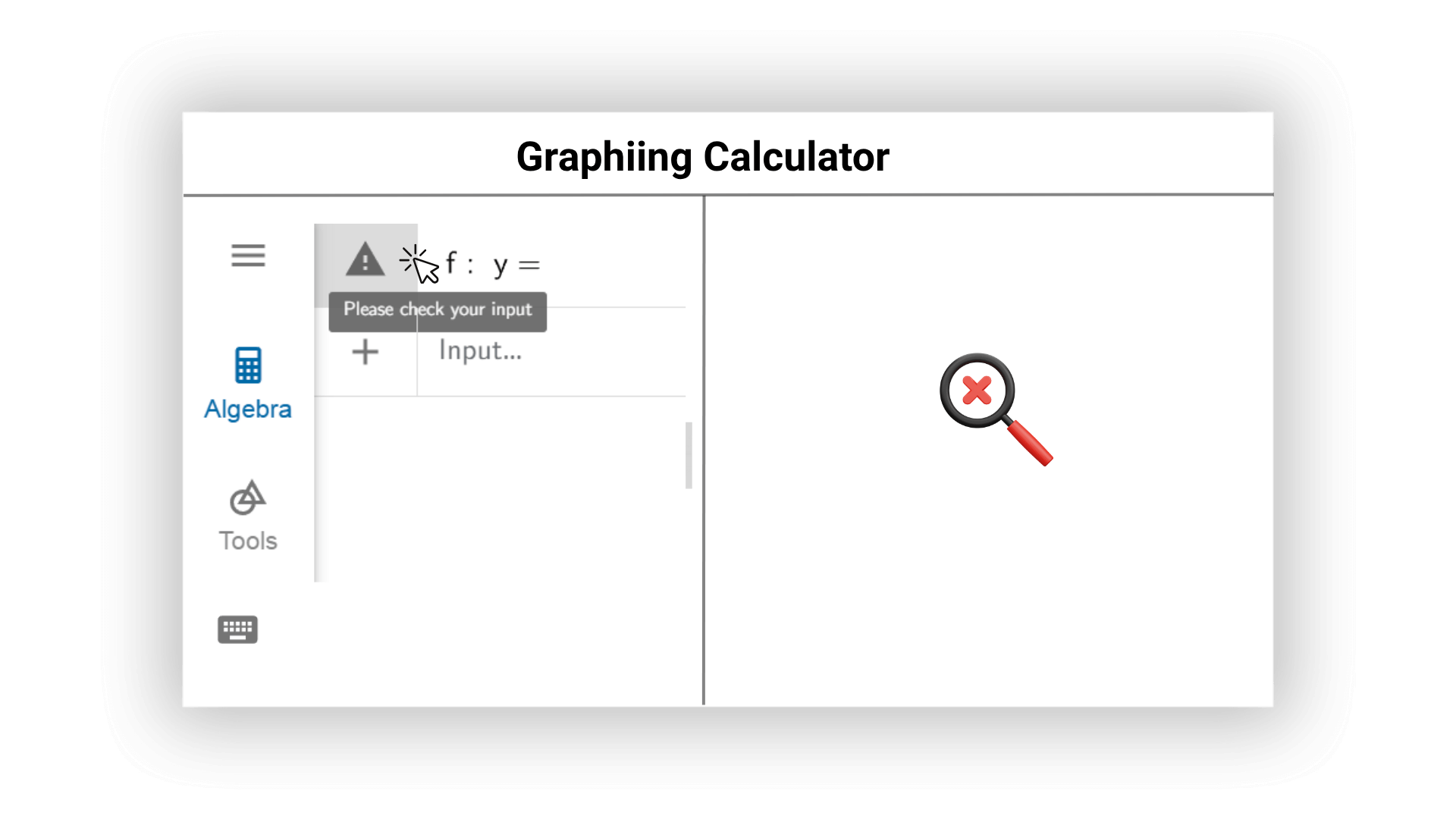
Nossa calculadora de gráficos de IA pode verificar possíveis erros em expressões matemáticas online em tempo real e dar sugestões proativamente para modificação. A IA pode lembrar prontamente os usuários de problemas gramaticais e entradas não razoáveis para garantir resultados de cálculo precisos e alta eficiência computacional, e evitar erros em imagens e resultados.
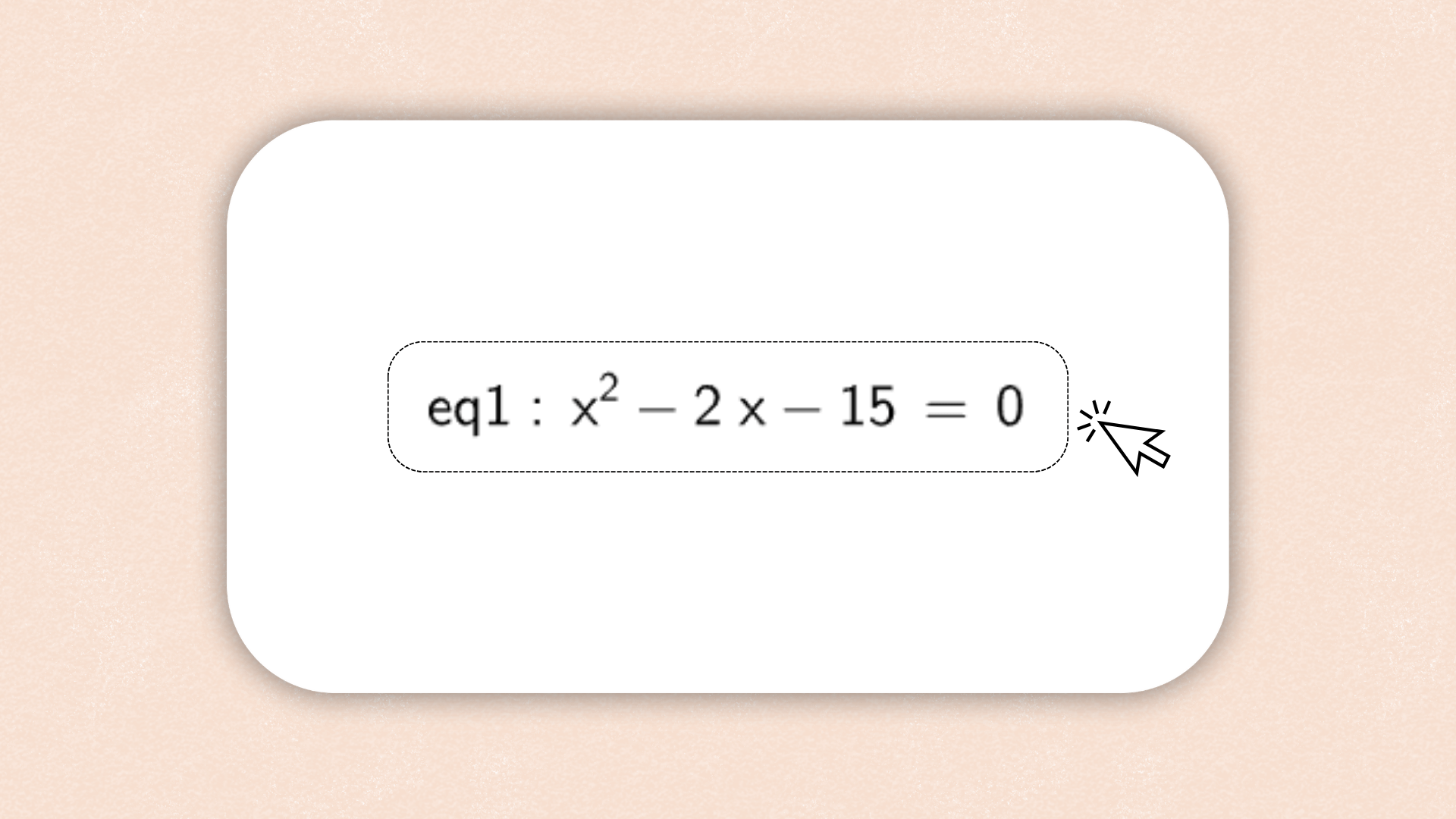
1. ![]() Digite
Digite y = m x + b na Barra de Entrada e
pressione Enter.
Dica: A Calculadora Gráfica
criará automaticamente controles deslizantes para os
parâmetros m e b ao pressionar Enter. Para mostrar os
controles deslizantes na Visualização Gráfica, selecione o
botão de Visibilidade desativado na Visualização Algébrica à
esquerda das variáveis.
2. ![]() Crie o ponto de interseção A entre a reta e o eixo y.
Crie o ponto de interseção A entre a reta e o eixo y.
Dica:
Você pode usar a ferramenta Interseção encontrada na Caixa
de Ferramentas para pontos, selecionando os dois objetos, ou
usar o comando Intersect(f, yAxis).
3. ![]() Crie um ponto B na origem usando a ferramenta Interseção e
selecionando os dois eixos.
Crie um ponto B na origem usando a ferramenta Interseção e
selecionando os dois eixos.
4. ![]() Selecione a ferramenta Segmento na Caixa de Ferramentas
para retas e crie um segmento entre os pontos A e B
selecionando ambos.
Selecione a ferramenta Segmento na Caixa de Ferramentas
para retas e crie um segmento entre os pontos A e B
selecionando ambos.
Dica: Alternativamente, você
também pode usar o comando Segment(A, B).
5. ![]() Oculte os pontos A e B clicando nos botões de Visibilidade
ativados à esquerda de suas coordenadas na Visualização
Algébrica.
Oculte os pontos A e B clicando nos botões de Visibilidade
ativados à esquerda de suas coordenadas na Visualização
Algébrica.
6. ![]() Use a ferramenta Inclinação na Caixa de Ferramentas de
Medidas para criar a inclinação (triângulo) da reta clicando
sobre ela.
Use a ferramenta Inclinação na Caixa de Ferramentas de
Medidas para criar a inclinação (triângulo) da reta clicando
sobre ela.
7. ![]() Melhore a aparência da sua construção usando a Barra de
Estilo (por exemplo, aumente a espessura do segmento para
torná-lo visível sobre o eixo y).
Melhore a aparência da sua construção usando a Barra de
Estilo (por exemplo, aumente a espessura do segmento para
torná-lo visível sobre o eixo y).
1. ![]() Digite f(x) = x^2 na Barra de Entrada e pressione
Enter.
Digite f(x) = x^2 na Barra de Entrada e pressione
Enter.
Qual é o formato do gráfico da função?
2. ![]() Use a ferramenta Mover e selecione a função. Clique na
Barra de Estilo e selecione para destravar a função. Agora
você pode arrastar a função na Visualização Gráfica e
observar como a equação na Visualização Algébrica se adapta
às suas alterações.
Use a ferramenta Mover e selecione a função. Clique na
Barra de Estilo e selecione para destravar a função. Agora
você pode arrastar a função na Visualização Gráfica e
observar como a equação na Visualização Algébrica se adapta
às suas alterações.
3. ![]() Altere o gráfico da função para que a equação
correspondente seja:
Altere o gráfico da função para que a equação
correspondente seja:
f(x) = (x + 2)²
f(x) = x² - 3
e
f(x) = (x - 4)² + 2.
4. ![]() Selecione a equação do polinômio. Use o teclado para
alterar a equação para f(x) = 3 x^2.
Selecione a equação do polinômio. Use o teclado para
alterar a equação para f(x) = 3 x^2.
Como o
gráfico da função muda?
5. ![]() Repita a alteração da equação digitando diferentes valores
para o parâmetro (por exemplo, 0.5, -2, -0.8, 3).
Repita a alteração da equação digitando diferentes valores
para o parâmetro (por exemplo, 0.5, -2, -0.8, 3).
1. ![]() Digite f(x) = a*x³ + b*x² + c*x + d na Barra de
Entrada e pressione Enter.
Digite f(x) = a*x³ + b*x² + c*x + d na Barra de
Entrada e pressione Enter.
Dica: A Calculadora Gráfica criará automaticamente
controles deslizantes para os parâmetros a, b, c e d.
2. ![]() Mostre os controles deslizantes na Visualização Gráfica
selecionando os botões de Visibilidade desativados à
esquerda das respectivas entradas na Visualização
Algébrica.
Mostre os controles deslizantes na Visualização Gráfica
selecionando os botões de Visibilidade desativados à
esquerda das respectivas entradas na Visualização
Algébrica.
3. ![]() Use os controles deslizantes na Visualização Gráfica para
alterar os valores dos parâmetros com a ferramenta Mover
para a = 0.2, b = -1.2, c = 0.6, d = 2.
Use os controles deslizantes na Visualização Gráfica para
alterar os valores dos parâmetros com a ferramenta Mover
para a = 0.2, b = -1.2, c = 0.6, d = 2.
4. ![]() Digite R = Root(f) na Barra de Entrada para exibir
as raízes do polinômio. As raízes serão automaticamente
nomeadas R1, R2 e R3.
Digite R = Root(f) na Barra de Entrada para exibir
as raízes do polinômio. As raízes serão automaticamente
nomeadas R1, R2 e R3.
5. ![]() Digite E = Extremum(f) para exibir os extremos
locais do polinômio.
Digite E = Extremum(f) para exibir os extremos
locais do polinômio.
6. ![]() Use a ferramenta Tangente para criar as tangentes ao
polinômio passando pelos extremos E1 e E2.
Use a ferramenta Tangente para criar as tangentes ao
polinômio passando pelos extremos E1 e E2.
Dica: Abra a Caixa de Ferramentas de Retas
Especiais e selecione a ferramenta Tangente. Selecione
sucessivamente o ponto E1 e o polinômio para criar a
tangente. Repita para o ponto E2.
7. ![]() Altere sistematicamente os valores dos controles
deslizantes usando a ferramenta Mover para explorar como os
parâmetros afetam o polinômio.
Altere sistematicamente os valores dos controles
deslizantes usando a ferramenta Mover para explorar como os
parâmetros afetam o polinômio.
1. ![]() Digite a equação linear linha_1: y = m_1 x + b_1 na
Barra de Entrada.
Digite a equação linear linha_1: y = m_1 x + b_1 na
Barra de Entrada.
Dica: O input linha_1 cria a linha1.
2. ![]() A Calculadora Gráfica criará automaticamente controles
deslizantes para as variáveis m_1 e b_1 ao
pressionar Enter.
A Calculadora Gráfica criará automaticamente controles
deslizantes para as variáveis m_1 e b_1 ao
pressionar Enter.
3. ![]() Mostre os controles deslizantes na Visualização Gráfica
clicando nos botões de Visibilidade desativados ao lado da
entrada na Visualização Algébrica.
Mostre os controles deslizantes na Visualização Gráfica
clicando nos botões de Visibilidade desativados ao lado da
entrada na Visualização Algébrica.
4. ![]() Repita os passos 1 a 3 para a equação de
linha_2: y = m_2 x + b_2.
Repita os passos 1 a 3 para a equação de
linha_2: y = m_2 x + b_2.
5. ![]() Use a Barra de Estilo para alterar a cor de ambas as linhas
e seus controles deslizantes.
Use a Barra de Estilo para alterar a cor de ambas as linhas
e seus controles deslizantes.
6. ![]() Use a ferramenta Texto e crie um texto dinâmico digitando
Linha 1: na caixa de diálogo que aparece e
selecionando linha_1 na lista de objetos na aba
Objetos da seção Avançado.
Use a ferramenta Texto e crie um texto dinâmico digitando
Linha 1: na caixa de diálogo que aparece e
selecionando linha_1 na lista de objetos na aba
Objetos da seção Avançado.
7. ![]() Crie um texto dinâmico com a parte estática
Linha 2: e selecione linha_2 na lista de
objetos na aba Objetos da seção Avançado.
Crie um texto dinâmico com a parte estática
Linha 2: e selecione linha_2 na lista de
objetos na aba Objetos da seção Avançado.
8. ![]() Use a Barra de Estilo para combinar a cor dos textos com
suas respectivas linhas.
Use a Barra de Estilo para combinar a cor dos textos com
suas respectivas linhas.
9. ![]() Construa o ponto de interseção A de linha_1 e
linha_2 usando a ferramenta Interseção ou digitando o
comando Intersect(linha_1, linha_2) na Barra de
Entrada.
Construa o ponto de interseção A de linha_1 e
linha_2 usando a ferramenta Interseção ou digitando o
comando Intersect(linha_1, linha_2) na Barra de
Entrada.
10. ![]() Digite xcoordenada = x(A) na Barra de Entrada.
Digite xcoordenada = x(A) na Barra de Entrada.
Dica: x(A) retorna a coordenada x do ponto de
interseção A.
11. ![]() Defina também ycoordenada = y(A).
Defina também ycoordenada = y(A).
Dica: y(A) retorna a coordenada y do ponto de
interseção A.
12. ![]() Crie um texto dinâmico com a parte estática
Solução: x = e selecione xcoordenada na lista
de objetos na aba Objetos.
Crie um texto dinâmico com a parte estática
Solução: x = e selecione xcoordenada na lista
de objetos na aba Objetos.
13. ![]() Crie um texto dinâmico com a parte estática y = e
selecione ycoordenada na lista de objetos na aba
Objetos.
Crie um texto dinâmico com a parte estática y = e
selecione ycoordenada na lista de objetos na aba
Objetos.
14. ![]() Fixe os textos para que não possam ser movidos
acidentalmente selecionando-os e abrindo a Barra de
Estilo.
Fixe os textos para que não possam ser movidos
acidentalmente selecionando-os e abrindo a Barra de
Estilo.
1. ![]() Digite o polinômio f(x) = x^2/2 + 1 na Barra de
Entrada.
Digite o polinômio f(x) = x^2/2 + 1 na Barra de
Entrada.
2. ![]() Crie um novo ponto A na função f.
Crie um novo ponto A na função f.
Dica: O ponto A só pode ser movido ao longo da
função.
3. ![]() Crie a tangente g à função f passando pelo
ponto A.
Crie a tangente g à função f passando pelo
ponto A.
4. ![]() Crie a inclinação da tangente g usando
m = Slope(g).
Crie a inclinação da tangente g usando
m = Slope(g).
5. ![]() Defina o ponto S = (x(A), m).
Defina o ponto S = (x(A), m).
Dica: x(A) retorna a coordenada x do ponto A.
6. ![]() Conecte os pontos A e S usando um
segmento.
Conecte os pontos A e S usando um
segmento.
7. ![]() Ative o rastro do ponto S e mova o ponto
A.
Ative o rastro do ponto S e mova o ponto
A.
Dica: Clique com o botão direito no ponto S
(MacOS: Ctrl-clique, tablet: toque longo) e selecione
Mostrar Rastro.
1. ![]() Digite a função f(x) = sin(x) na Barra de
Entrada.
Digite a função f(x) = sin(x) na Barra de
Entrada.
2. ![]() Clique com o botão direito na Visualização Gráfica e
selecione Gráficos... . Selecione a aba xEixo e altere a
unidade para
Clique com o botão direito na Visualização Gráfica e
selecione Gráficos... . Selecione a aba xEixo e altere a
unidade para π.
3. ![]() Crie um novo ponto A na função f.
Crie um novo ponto A na função f.
Dica: O ponto A só pode ser movido ao longo da
função.
4. ![]() Crie a tangente g à função f passando pelo
ponto A.
Crie a tangente g à função f passando pelo
ponto A.
5. ![]() Crie a inclinação da tangente g usando a ferramenta
Inclinação.
Crie a inclinação da tangente g usando a ferramenta
Inclinação.
6. ![]() Defina o ponto S = (x(A), m).
Defina o ponto S = (x(A), m).
Dica: x(A) retorna a coordenada x do ponto A.
7. ![]() Conecte os pontos A e S usando um
segmento.
Conecte os pontos A e S usando um
segmento.
8. ![]() Ative o rastro do ponto S e mova o ponto
A.
Ative o rastro do ponto S e mova o ponto
A.
Dica: Clique com o botão direito no ponto S
(MacOS: Ctrl-clique, tablet: toque longo) e selecione
Mostrar Rastro.
9. ![]() Clique com o botão direito (MacOS: Ctrl-clique, tablet:
toque longo) no ponto A e escolha Animação no
menu de contexto.
Clique com o botão direito (MacOS: Ctrl-clique, tablet:
toque longo) no ponto A e escolha Animação no
menu de contexto.
Dica: Um botão de Animação aparece no canto
inferior esquerdo da Visualização Gráfica. Ele permite
pausar ou continuar a animação.
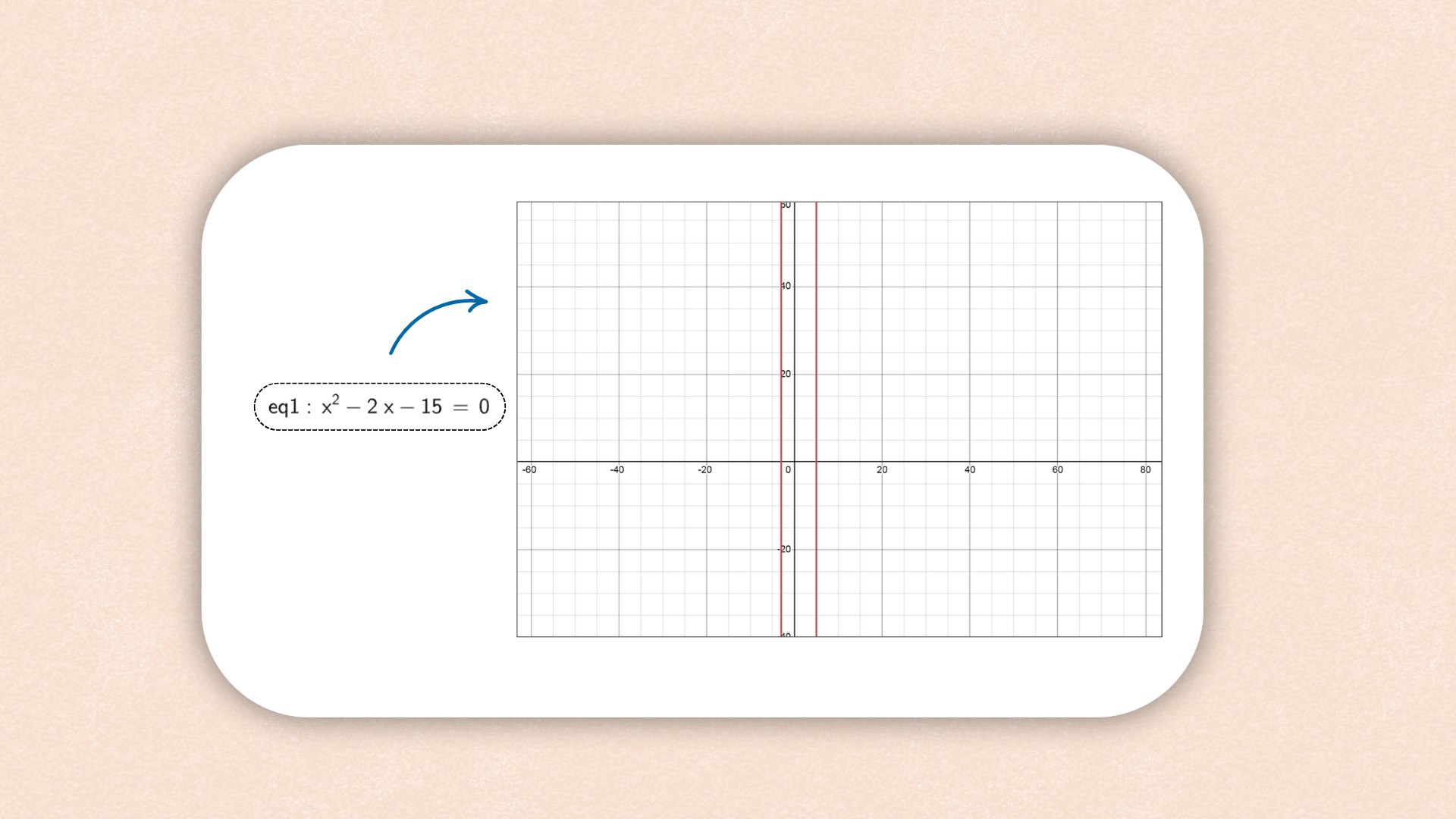
1. ![]() Digite a x + b y ≤ c na Barra de Entrada e pressione
Enter.
Digite a x + b y ≤ c na Barra de Entrada e pressione
Enter.
Dica: Você pode usar o Teclado Virtual
para inserir o símbolo ≤. A Calculadora Gráfica criará
automaticamente controles deslizantes para os parâmetros a,
b e c.
2. ![]() Use a ferramenta Mover para ajustar os valores dos
controles deslizantes para que a = 1, b = 1 e c = 3.
Use a ferramenta Mover para ajustar os valores dos
controles deslizantes para que a = 1, b = 1 e c = 3.
3. ![]() Altere o incremento dos controles deslizantes para 1.
Altere o incremento dos controles deslizantes para 1.
Dica:
Selecione o número a e abra a Barra de Estilo da
Visualização Gráfica.
Abra as configurações do número a
e selecione a aba Controle Deslizante.
Defina o
incremento para 1 e repita para os números b e c.
4. ![]() Arraste o fundo da Visualização Gráfica para mover a origem
para o centro.
Arraste o fundo da Visualização Gráfica para mover a origem
para o centro.
5. ![]() Reduza o zoom para tornar uma parte maior do sistema de
coordenadas visível na tela.
Reduza o zoom para tornar uma parte maior do sistema de
coordenadas visível na tela.
6. ![]() Defina a distância entre as marcas nos eixos para 1.
Defina a distância entre as marcas nos eixos para 1.
Dica:
Certifique-se de que nenhum objeto esteja selecionado antes
de abrir a Barra de Estilo da Visualização Gráfica.
Abra
as configurações dos eixos.
Selecione a aba xEixo e
defina a distância para 1.
Repita na aba yEixo.
1. ![]() Digite
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) na
Barra de Entrada e pressione Enter.
Digite
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) na
Barra de Entrada e pressione Enter.
2. ![]() Crie um controle deslizante s para um número com
intervalo de 1 a 10 e incremento 1.
Crie um controle deslizante s para um número com
intervalo de 1 a 10 e incremento 1.
3. ![]() Digite Sequence((i, i), i, 0, s) na Barra de Entrada
e pressione Enter.
Digite Sequence((i, i), i, 0, s) na Barra de Entrada
e pressione Enter.
4. ![]() Mova o controle deslizante s para verificar a
construção.
Mova o controle deslizante s para verificar a
construção.
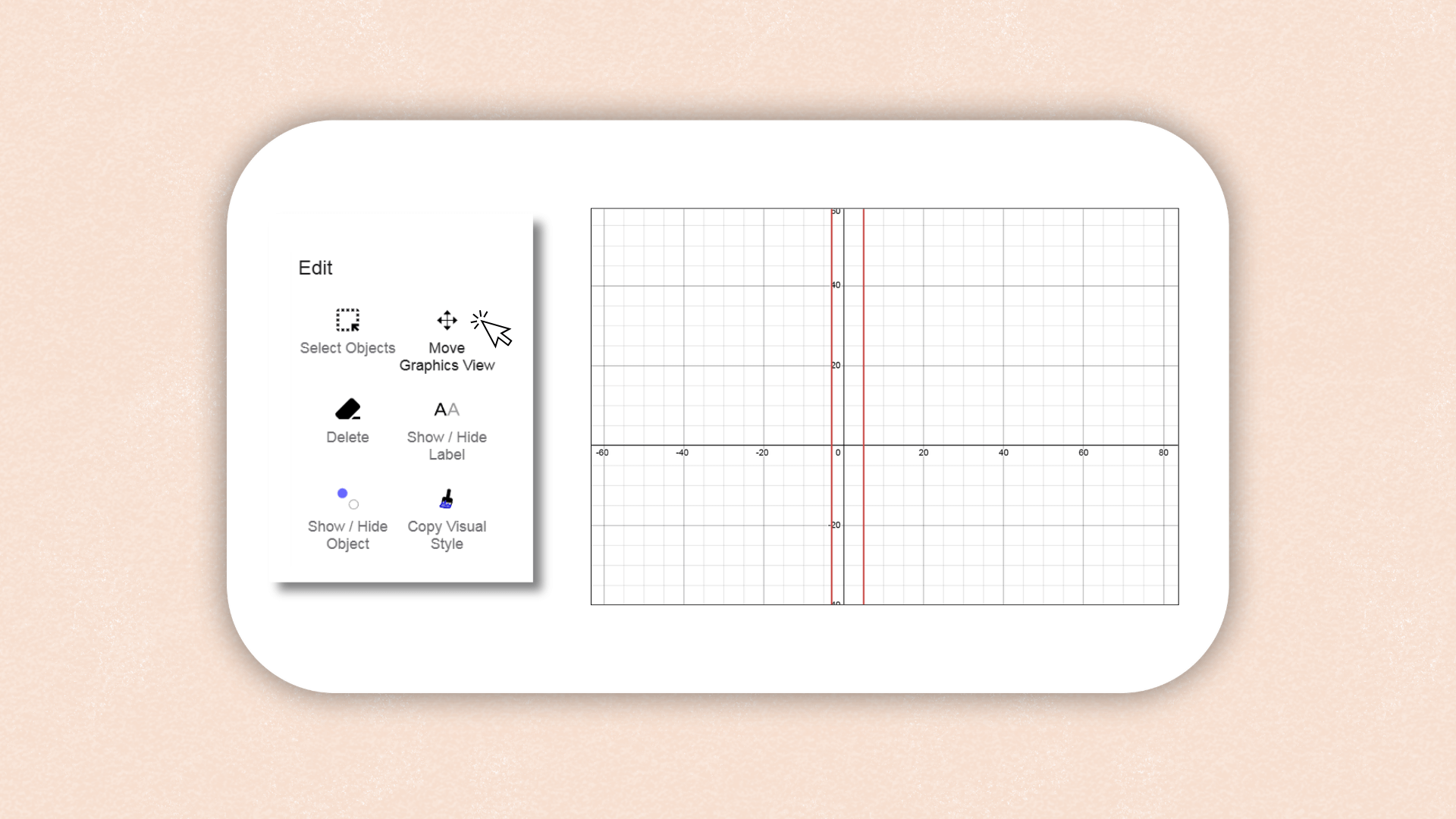
1. ![]() Abra as Configurações da Visualização Gráfica usando a
Barra de Estilo.
Abra as Configurações da Visualização Gráfica usando a
Barra de Estilo.
2. ![]() Na aba xEixo, defina a distância das marcas para 1 marcando
a caixa Distância e inserindo 1 no campo de texto.
Na aba xEixo, defina a distância das marcas para 1 marcando
a caixa Distância e inserindo 1 no campo de texto.
3. ![]() Na aba Básico, defina o mínimo do xEixo para -11 e o máximo
para 11.
Na aba Básico, defina o mínimo do xEixo para -11 e o máximo
para 11.
4. ![]() Na aba yEixo, desmarque Mostrar yEixo e feche as
Configurações.
Na aba yEixo, desmarque Mostrar yEixo e feche as
Configurações.
5. ![]() Crie dois controles deslizantes a e b, ambos
com intervalo de -5 a 5 e incremento 1.
Crie dois controles deslizantes a e b, ambos
com intervalo de -5 a 5 e incremento 1.
6. ![]() Mostre o valor dos controles deslizantes em vez de seus
nomes usando a Barra de Estilo.
Mostre o valor dos controles deslizantes em vez de seus
nomes usando a Barra de Estilo.
7. ![]() Crie os pontos A = (0, 1) e
B = A + (a, 0).
Crie os pontos A = (0, 1) e
B = A + (a, 0).
Dica: A distância do ponto B ao ponto A é
determinada pelo controle deslizante a.
8. ![]() Crie um vetor u = Vetor(A, B) que tem comprimento
a.
Crie um vetor u = Vetor(A, B) que tem comprimento
a.
9. ![]() Crie os pontos C = B + (0, 1) e
D = C + (b, 0).
Crie os pontos C = B + (0, 1) e
D = C + (b, 0).
10. ![]() Crie o vetor v = Vetor(C, D) que tem comprimento
b.
Crie o vetor v = Vetor(C, D) que tem comprimento
b.
11. ![]() Crie o ponto R = (x(D), 0).
Crie o ponto R = (x(D), 0).
Dica: O input x(D) retorna a coordenada x do ponto
D. Assim, o ponto R mostra o resultado da soma na reta
numérica.
12. ![]() Crie o ponto Z = (0, 0).
Crie o ponto Z = (0, 0).
13. ![]() Crie três segmentos c = Segmento(Z, A),
d = Segmento(B, C) e e = Segmento(D, R).
Crie três segmentos c = Segmento(Z, A),
d = Segmento(B, C) e e = Segmento(D, R).
14. ![]() Use a Barra de Estilo para aprimorar sua construção (por
exemplo, combine a cor dos controles deslizantes e vetores,
altere o estilo da linha, fixe controles deslizantes, oculte
rótulos e pontos).
Use a Barra de Estilo para aprimorar sua construção (por
exemplo, combine a cor dos controles deslizantes e vetores,
altere o estilo da linha, fixe controles deslizantes, oculte
rótulos e pontos).
1. ![]() Crie um controle deslizante horizontal chamado
Colunas para um número com intervalo de 1 a 10,
incremento 1 e largura 300.
Crie um controle deslizante horizontal chamado
Colunas para um número com intervalo de 1 a 10,
incremento 1 e largura 300.
Dica: Você pode
alterar a largura do controle deslizante na aba
Configurações em Controle Deslizante.
2. ![]() Crie um novo ponto A.
Crie um novo ponto A.
3. ![]() Construa o segmento f com o comprimento
Colunas a partir do ponto A.
Construa o segmento f com o comprimento
Colunas a partir do ponto A.
4. ![]() Mova o controle deslizante Colunas para observar o segmento
com o comprimento especificado.
Mova o controle deslizante Colunas para observar o segmento
com o comprimento especificado.
5. ![]() Construa uma reta perpendicular g ao segmento f
passando pelo ponto A.
Construa uma reta perpendicular g ao segmento f
passando pelo ponto A.
6. ![]() Construa uma reta perpendicular h ao segmento f
passando pelo ponto B.
Construa uma reta perpendicular h ao segmento f
passando pelo ponto B.
7. ![]() Crie um controle deslizante vertical chamado
Linhas para um número com intervalo de 1 a 10,
incremento 1 e largura 300.
Crie um controle deslizante vertical chamado
Linhas para um número com intervalo de 1 a 10,
incremento 1 e largura 300.
Dica: Você pode
selecionar a orientação do controle deslizante na caixa de
diálogo Controle Deslizante na aba Controle
Deslizante.
8. ![]() Crie um círculo c com centro em A e raio
Linhas.
Crie um círculo c com centro em A e raio
Linhas.
9. ![]() Mova o controle deslizante Linhas para observar o círculo
com o raio especificado.
Mova o controle deslizante Linhas para observar o círculo
com o raio especificado.
10. ![]() Interseccione o círculo c com a reta g para obter o ponto
de interseção C.
Interseccione o círculo c com a reta g para obter o ponto
de interseção C.
Dica: Ao selecionar a
ferramenta Interseção, clique no ponto de interseção acima
do ponto A para criar apenas esse ponto.
11. ![]() Crie uma reta paralela i ao segmento f passando pelo
ponto de interseção C.
Crie uma reta paralela i ao segmento f passando pelo
ponto de interseção C.
12. ![]() Interseccione as retas i e h para obter o ponto de
interseção D.
Interseccione as retas i e h para obter o ponto de
interseção D.
13. ![]() Construa um polígono ABDC.
Construa um polígono ABDC.
14. ![]() Oculte todas as retas, o círculo c e o segmento f.
Oculte todas as retas, o círculo c e o segmento f.
15. ![]() Oculte os rótulos dos segmentos usando a Barra de
Estilo.
Oculte os rótulos dos segmentos usando a Barra de
Estilo.
16. ![]() Defina ambos os controles deslizantes Colunas e Linhas para
o valor 10.
Defina ambos os controles deslizantes Colunas e Linhas para
o valor 10.
17. ![]() Crie uma lista de segmentos verticais usando:
Crie uma lista de segmentos verticais usando:Sequence(Segment(A + i*(1, 0), C + i*(1, 0)), i, 1,
Colunas)
Nota: A + i*(1, 0) especifica uma série de pontos
começando em A com distância 1 entre eles.
C + i*(1, 0)
especifica uma série de pontos começando em C com distância
1 entre eles.
Segment(A + i*(1, 0), C + i*(1, 0)) cria
uma lista de segmentos entre pares desses pontos. Note que
os pontos finais dos segmentos não são mostrados na
Visualização Gráfica.
O controle deslizante Colunas
determina o número de segmentos criados.
18. ![]() Crie uma lista de segmentos horizontais.
Crie uma lista de segmentos horizontais.Sequence(Segment(A + i*(0, 1), B + i*(0, 1)), i, 1,
Linhas)
19. ![]() Mova os controles deslizantes Colunas e Linhas para
observar a construção.
Mova os controles deslizantes Colunas e Linhas para
observar a construção.
20. ![]() Insira textos estáticos e dinâmicos para enunciar o
problema de multiplicação usando os valores de Colunas e
Linhas como fatores:
Insira textos estáticos e dinâmicos para enunciar o
problema de multiplicação usando os valores de Colunas e
Linhas como fatores:texto1: Colunastexto2: *texto3: Linhastexto4: =
21. ![]() Calcule o resultado da multiplicação:
Calcule o resultado da multiplicação:
resultado = Colunas * Linhas
22. ![]() Insira texto dinâmico5:
Insira texto dinâmico5: resultado
23. ![]() Oculte os pontos A, B, C e D.
Oculte os pontos A, B, C e D.
24. ![]() Aprimore sua construção usando a Barra de Estilo.
Aprimore sua construção usando a Barra de Estilo.
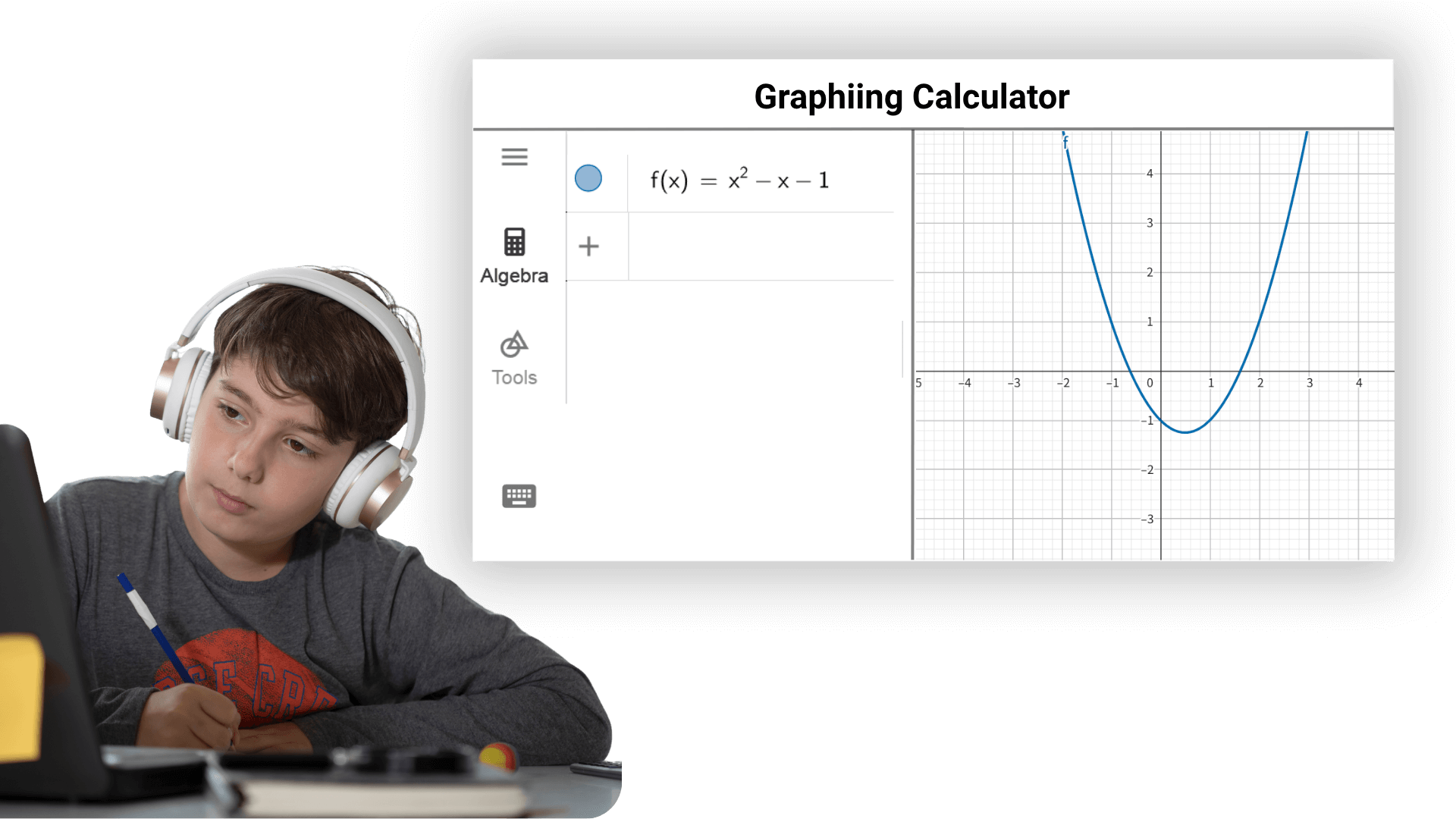
A calculadora gráfica de IA é uma poderosa assistente para os alunos aprenderem matemática. Do ensino médio à universidade, são os cursos de álgebra, geometria, cálculo ou estatística que podem ajudar os alunos a entender e dominar melhor o conhecimento matemático e melhorar a eficiência e as notas de aprendizagem. Os professores podem usá-la para conduzir demonstrações de ensino e criar materiais de ensino vívidos para estimular o interesse e o entusiasmo dos alunos pela aprendizagem.
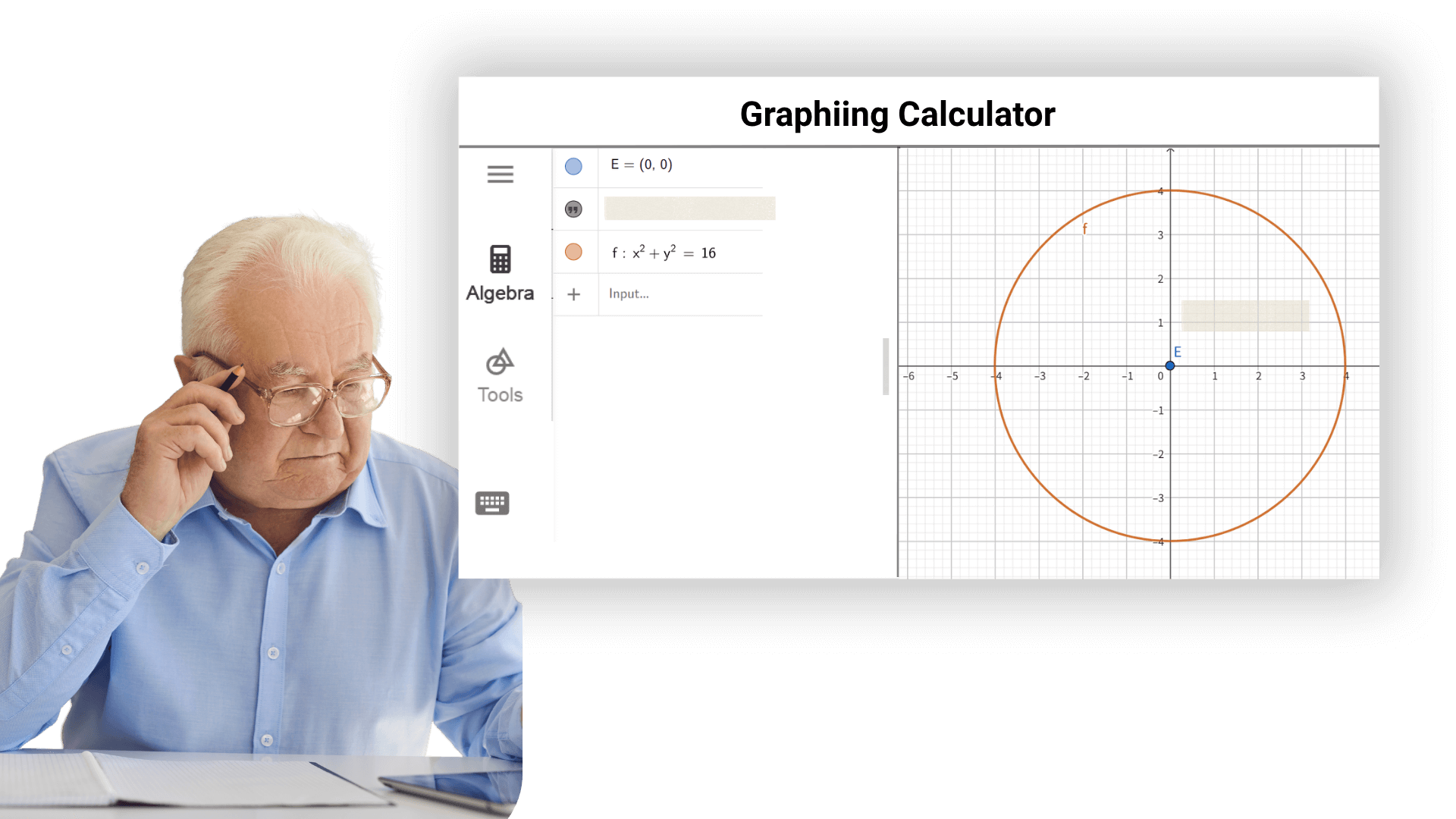
Ele fornece aos pesquisadores poderosas ferramentas matemáticas para facilitar o processamento de dados, análise experimental, construção de modelos e verificação teórica. Em vários campos científicos como física, química, biologia e engenharia, as calculadoras gráficas podem ser usadas para completar rapidamente e com precisão operações matemáticas complexas e análise de dados, auxiliando no desenvolvimento suave da pesquisa científica.
Use a calculadora gráfica para desenhar curvas de oferta e demanda, modelos de crescimento composto, etc, analise a interseção das funções de custo marginal e receita, e auxilie na tomada de decisões de negócios.
A Calculadora Gráfica beneficia estudantes desde o ensino fundamental até o universitário. Ela ajuda a compreender conceitos matemáticos e cultiva habilidades de resolução de problemas.

Professores de matemática podem usar a calculadora gráfica para criar materiais de ensino e demonstrar conceitos e processos de resolução de problemas, melhorando a eficácia do ensino e a interação.

Pesquisadores em vários campos confiam nela para cálculos matemáticos complexos e análise de dados. A calculadora gráfica online fornece resultados precisos, acelerando a pesquisa.

Diga adeus ao desenho manual tedioso, gere gráficos de visualização de dados profissionais com um clique, desenhe gráficos de funções online, anote a média e a variância em tempo real, ajuste dinamicamente curvas de regressão, e complete eficientemente a integração e análise de dados.

As calculadoras gráficas ajudam engenheiros de software a visualizar algoritmos de filtro e otimizar parâmetros de renderização, garantindo o desempenho perfeito de funções.

Para designers arquitetônicos, as calculadoras gráficas são potências de design paramétrico, insira equações de curvas para gerar gráficos de função/deslocamento, valide visualmente a mecânica estrutural, e reduza ciclos de design.

Todas as funções não requerem registro ou pagamento, e você pode usá-las a qualquer momento.
Mantenha alta precisão ao calcular problemas avançados, como determinantes de matriz e integrais, para evitar erros na pesquisa científica.
O cálculo é realizado inteiramente no navegador, nenhum dado é carregado e a página é limpa ao ser fechada.
Sem a necessidade de download e instalação, os telefones móveis e computadores podem ser usados imediatamente.
Concentre-se na essência do aprendizado, sem pop-ups, sem anúncios, e melhore a concentração.
Seja para aplicações acadêmicas, pesquisas científicas, escritório ou engenharia, podemos atender às suas necessidades de computação gráfica.
Você não precisa se registrar ou baixar nenhum software. Apenas entre no nosso site em seu navegador e comece a usar essa poderosa ferramenta de calculadora gráfica. Você pode experimentar sua conveniência instantaneamente.
Sim, nossa calculadora gráfica de IA é completamente gratuita. Apesar de ser gratuita, não restringe nenhuma das suas principais características. Você pode usar integralmente suas funções de graficagem, cálculo e análise de dados sem nenhum custo. Nossa meta é fornecer uma ferramenta matemática conveniente e eficiente para todos.
Nós priorizamos a segurança e a privacidade dos seus dados. Todas as suas calculações, gráficos e dados de entrada são processados localmente em seu navegador e nunca são carregados ou armazenados em nossos servidores. Você pode usar com confiança, sabendo que seus dados estão seguros.
Para entrar uma função, simplesmente digite a fórmula na caixa de entrada na página inicial. Por exemplo, entre "y=2x^2" ou "f(x)=sen(x)". A calculadora automaticamente processará sua entrada e exibirá o gráfico.
Sim, a Calculadora Gráfica de IA pode lidar com uma variedade de funções, desde equações lineares simples até avançadas como integrais, derivadas e equações multivariáveis. É adequada para necessidades matemáticas básicas e avançadas, tornando-a ideal para estudantes e profissionais.
Sim, é completamente acessível em dispositivos móveis. Você pode usá-la em smartphones ou tablets, e está otimizada para todos os tamanhos de tela, garantindo uma experiência sem interrupções onde você estiver.