Бесплатный калькулятор уравнений | Решение уравнений онлайн
Пошаговый калькулятор уравнений и неравенств. Бесплатное решение уравнений онлайн по фото или вводу для школьников и студентов.
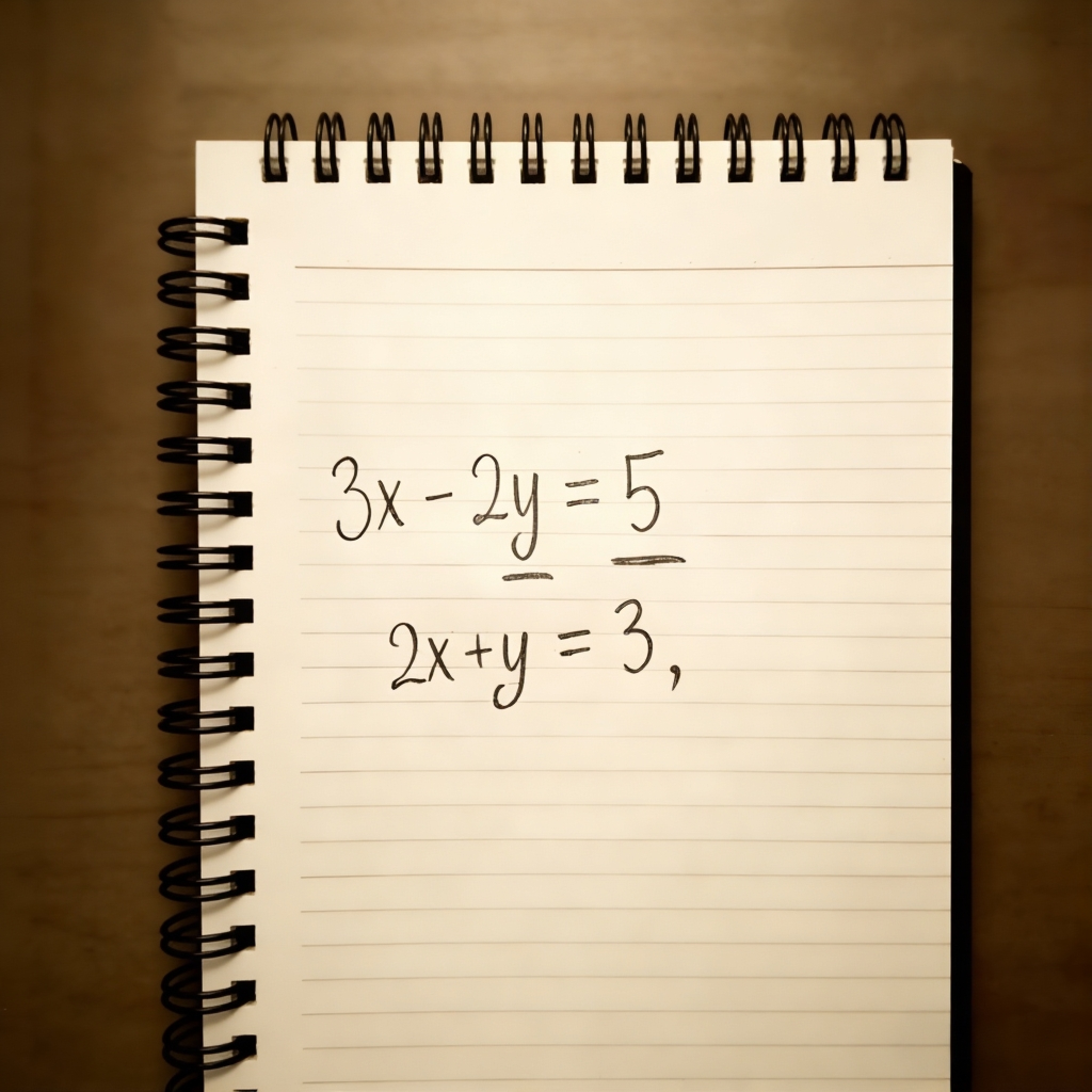
Что такое уравнение?
Уравнение, это математическое равенство с неизвестной переменной,
решение которого позволяет решить уравнение и найти значение этой
переменной. Уравнения устанавливают связь между известными и
неизвестными величинами.
Среди самых распространённых
типов, линейные уравнения, квадратные уравнения,
тригонометрические уравнения, логарифмические уравнения и
уравнения третьей степени.
Решение уравнений широко
применяется в домашней задаче по математике, а также в физике,
инженерии и экономике, везде, где требуется понять или рассчитать
реальные процессы.
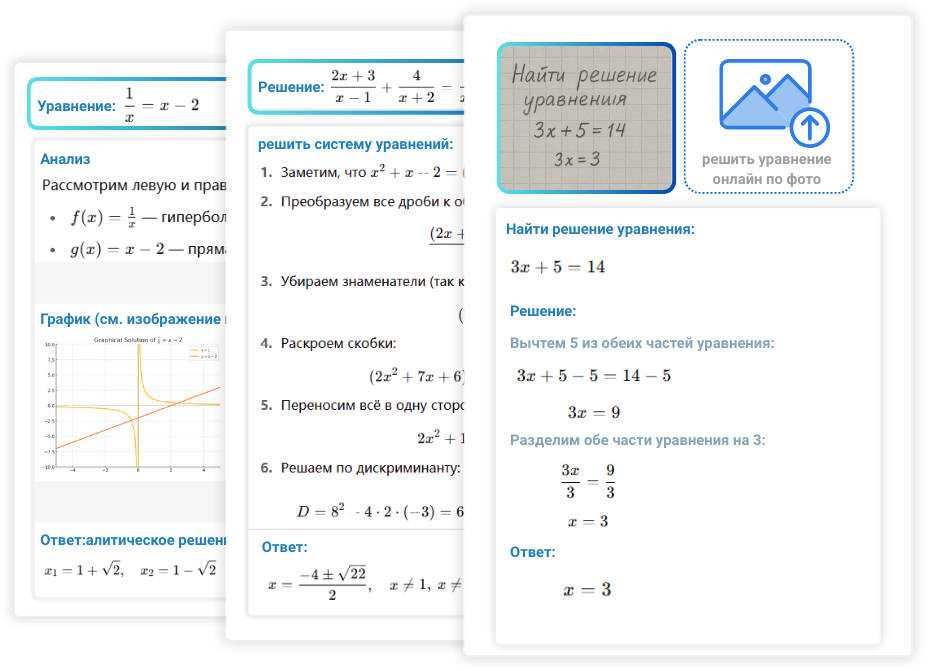
Что такое калькулятор уравнений?
Калькулятор уравнений , это инструмент на базе искусственного интеллекта для решения математических задач. Он использует алгоритмический анализ, чтобы помочь пользователям быстро и точно решить уравнение и решать системы уравнений онлайн. Пользователь может ввести уравнение онлайн вручную или загрузить фотографию, содержащую задачу решите уравнение онлайн по фото. Калькулятор автоматически распознаёт выражение и применяет стандартные математические методы для решения, предоставляя результат в виде пошагового объяснения.
Как решаются уравнения?
Решение уравнений традиционно требует ручного составления,
преобразования и вычислений, включая методы разложения на
множители, дискриминанта и метод Гаусса. Для уравнений более
высокой степени или сложных нелинейных систем уравнений онлайн
необходимы более продвинутые математические подходы и численные
методы.
С помощью калькулятора уравнений онлайн
достаточно просто решить уравнение онлайн по фото или ввести его
вручную, AI-калькулятор уравнений мгновенно выдаёт точный
результат. Более того, чтобы пользователю было легче понять
процесс, калькулятор уравнений моделирует человеческий подход к
решению: использует методы подстановки, исключения, формулы корней
и пошагово показывает весь ход решения.
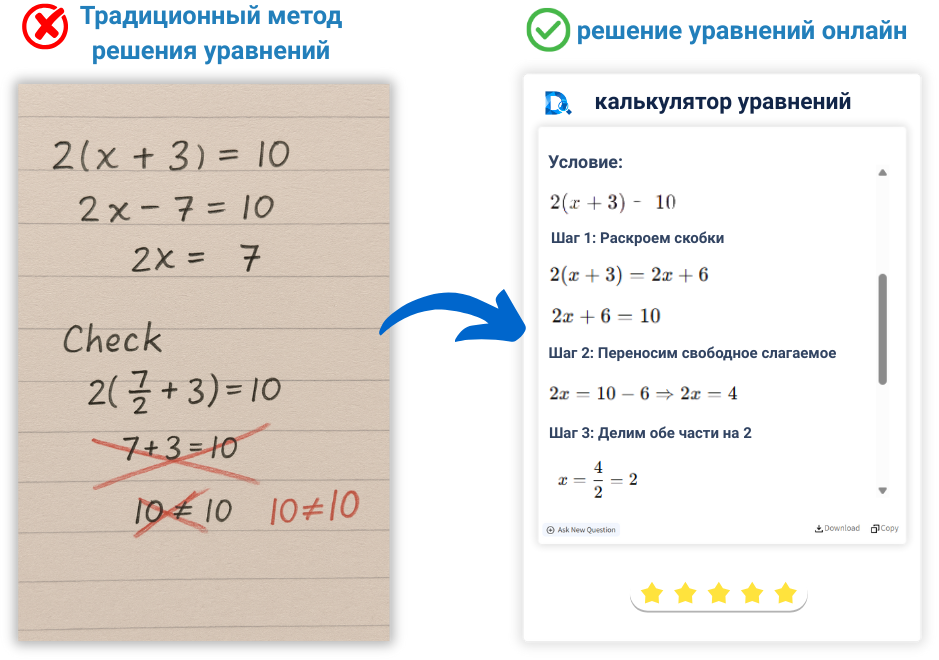
Как работает калькулятор уравнений?
Калькулятор уравнений использует ИИ-движок, основанный на алгебре,
численных методах и алгоритмическом анализе. При вводе или
загрузке уравнения онлайн система распознаёт формат, определяет
тип уравнения (линейное, квадратное, тригонометрическое,
логарифмическое и др.) и выбирает метод решения:
Линейные
уравнения и системы уравнений онлайн решаются через метод Гаусса
или матричный подход.
Квадратные, с помощью формулы
корней.
Сложные типы, включая тригонометрические и
логарифмические, через преобразования и численные приближения.
Для
нелинейных систем, используются численные методы.
Калькулятор
систем уравнений предоставляет не только ответ, но и полное
решение уравнений онлайн с пошаговым объяснением, что помогает
глубже понять ход решения.
Функциональные возможности калькулятора уравнений
Решение уравнений онлайн быстро, без ошибок, по фото или вручную, с поддержкой всех типов и пошаговым разбором.
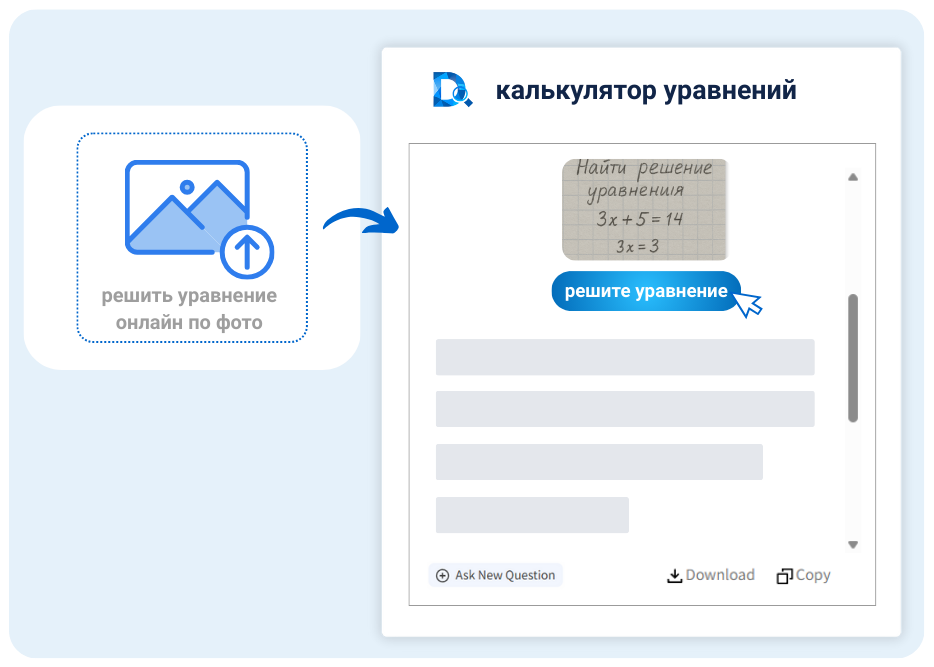
Решить уравнение онлайн по фото
Ручной ввод
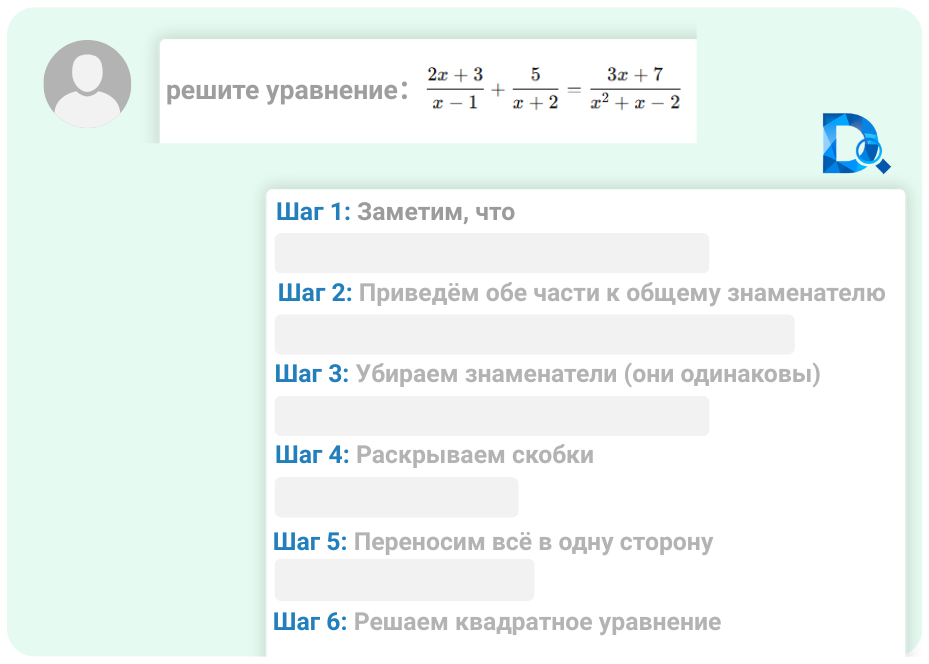
Пошаговый разбор
Поддержка различных типов уравнений
Решение неравенств и систем уравнений
Оптимизация для мобильных устройств
Калькулятор уравнений доступен в любое время и в любом месте
Мобильный удобный инструмент для решения уравнений онлайн с поддержкой фото ручного ввода и пошагового разбора.
Домашняя задание по математике
Подготовка к экзаменам
Поддержка на уроках
Проверка сложных решений
Проверка и подготовка учителем
Самостоятельное обучение
Поддерживаемые типы уравнений
Наш калькулятор может решать следующие типы математических уравнений. Независимо от сложности, вы получите подробное пошаговое решение.
| Тип уравнения | Общая форма | Особенности решения |
|---|---|---|
| Линейные уравнения | ax + b = 0 | Один корень, решается переносом и делением |
| Квадратные уравнения | ax² + bx + c = 0 | Формула корней, до двух решений |
| Биквадратные уравнения | x⁴ + bx² + c = 0 | Решение через замену переменной |
| Полиномиальные уравнения | aₙxⁿ + ... + a₀ = 0 | До n корней, действительных или комплексных |
| Логарифмические уравнения | log_b(f(x)) = g(x) | Решается через f(x) = b^g(x) |
| Показательные уравнения | a^{f(x)} = b^{g(x)} | Логарифмирование обеих частей |
| Уравнения с корнями | √f(x) = g(x) | Возведение в квадрат, проверка ОДЗ |
| Уравнения с модулем | |f(x)| = g(x) | Два случая: f(x)=g(x) и f(x)=-g(x) |
| Тригонометрические уравнения | sin(x), cos(x), ... | Используются периодичность и формулы |
| Комплексные уравнения | f(z) = 0 | Решение в комплексной плоскости |
| Матричные уравнения | AX = B | Методы линейной алгебры, обратные матрицы |
| Рациональные уравнения | P(x)/Q(x) = 0 | Решение с учётом допустимых значений |
| Целочисленные уравнения | ⌊f(x)⌋ = g(x) | Решение в рамках целых промежутков |
| Построение по корням | f(x) = (x − r₁)... | Построение многочлена по известным корням |
| Построение по точкам | f(x) через (x₁, y₁)... | Интерполяция |
| Численные методы | f(x) = 0 | Метод Ньютона и др. |
| Дифференциальные уравнения | y', y'' = f(x) | Решение для функции y(x) |
Как использовать калькулятор уравнений
-
1
Откройте сайт и перейдите на страницу калькулятора уравнений.
-
2
Загрузите фото или вручную введите уравнение онлайн.
-
3
Нажмите кнопку начала, система автоматически выполнит решение уравнений онлайн.
-
4
Просмотрите пошаговый разбор или задайте дополнительный вопрос.
Кто использует калькулятор уравнений онлайн
От начальной школы до вуза решайте уравнения быстро, точно и с поддержкой экзаменов ОГЭ и ЕГЭ.
Учащиеся начальной школы
Для базовой математической подготовки и развития раннего алгебраического мышления с помощью решения уравнений онлайн.
Школьники и выпускники (ОГЭ, ЕГЭ)
Разработан с учётом требований экзаменов ОГЭ и ЕГЭ. Поддерживает типовые задания по алгебре, функциям и тригонометрическим уравнениям.
Студенты вузов
Подходит для высшей математики, математического анализа и линейной алгебры. Помогает решать сложные функции и системы уравнений онлайн.
Самостоятельные ученики и энтузиасты
Для взрослых, стремящихся развить математическое мышление и логическое структурирование. Поддержка русского языка и локализованных математических терминов.
Преподаватели и репетиторы
В помощь при подготовке занятий, проверке домашней задачи по математике и демонстрации стандартных решений.
Аспиранты и зарубежные студенты
Для подготовки к вступительным испытаниям в магистратуру и международным тестам, где требуется быстро решить уравнение онлайн и проверить ответ.
Почему стоит использовать наш калькулятор уравнений
Полностью бесплатный
без регистрации и рекламы, решение уравнений онлайн без скрытых платежей.
Точный и надёжный расчёт
работа на основе интеллектуального алгоритма, точно обрабатывает любые уравнения.
Простой и эффективный в использовании
даже новичок легко сможет воспользоваться калькулятором уравнений.
Поддержка разных языков
Калькулятор распознаёт уравнения на 8 языках, подходит для международных экзаменов.
Без скачивания
не требует установки приложения, доступен в виде калькулятора онлайн прямо в браузере.
Поддержка всех типов уравнений
Решает основные типы уравнений и систем(линейные, квадратные, тригонометрические и др).
Что говорят наши пользователи
Часто задаваемые вопросы (FAQ)
Разные типы уравнений онлайн требуют разных подходов к решению:
1. Метод подстановки:
применяется для решения систем уравнений онлайн с двумя
неизвестными;
2. Метод исключения: используется для
устранения переменных и получения частного решения;
3. Мтод выделения полного квадрата / формула корней:
подходит для квадратных уравнений;
4. Графический метод / численные методы:
применимы к уравнениям высокой степени или к тем, которые не имеют
аналитического решения.
5. Калькулятор уравнений:
подходит для быстрого решения сложных по структуре и трудоёмких
уравнений, предоставляя при этом подробный пошаговый процесс.
Метод выделения полного квадрата — это приём решения квадратного
уравнения, имеющего вид
𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0.
Он заключается в
преобразовании выражения к форме полного квадрата, например
(𝑥
+ 𝑑)² = 𝑒,
что позволяет более наглядно решить уравнение. Этот
способ особенно удобен для решения уравнений, в которых коэффициенты
сложно обрабатывать стандартными методами.
Самое важное правило при решении уравнений онлайн — сохранять равновесие между левой и правой частью уравнения онлайн.Что бы вы ни делали с одной стороной — прибавляли, вычитали, умножали или делили — вы должны выполнить ту же операцию и с другой стороной.В противном случае нарушается суть уравнения онлайн как равенства, и результат решите уравнение окажется неверным.
Шаги следующие:
1. Перенос членов: перенесите
неизвестные в одну часть уравнения, а постоянные члены — в
другую;
2. Упрощение: объедините подобные члены и
упростите выражение;
3. Решение: при помощи сложения,
вычитания, умножения или деления преобразуйте уравнение к виду𝑥 =
значение; всегда убедитесь, что каждое действие применяется к
обеим сторонам уравнение онлайн одновременно.
Упрощение — это базовая операция при решении уравнений, которая
обычно включает:
1. удаление скобок;
2. приведение
подобных слагаемых (например,3x + 2x = 5x);
3. соблюдение
порядка операций (PEMDAS: скобки → степени → умножение/деление →
сложение/вычитание),чтобы сделать уравнение онлайн более аккуратным
и удобным для решения уравнений онлайн.
1. Упрощение обеих сторон: объединение подобных членов,
раскрытие скобок.
2. Изоляция переменной: перенос всех
членов с переменной на одну сторону.
3. Нахождение значения переменной:
применение обратных операций для упрощения коэффициентов и получения
окончательного результата.
Достаточно ввести уравнение онлайн, система автоматически распознает переменные и структуру, используя интеллектуальные алгоритмы (такие как алгебраические преобразования, численные методы и другие) для решения уравнений онлайн, а затем показывает подробные шаги решения и обоснование каждого этапа. Это идеально подходит для обучения, проверки домашней задания по математике или проверки сложных примеров.
📘 Полный список поддерживаемых математических функций
Ознакомьтесь с синтаксисом и обозначениями, которые можно использовать в калькуляторе.
📂 Нажмите, чтобы открыть таблицу функций
| Функция | Описание |
|---|---|
| abs(x) | Модуль числа x |
| arccos(x) | Арккосинус от x |
| arccosh(x) | Гиперболический арккосинус |
| arcsin(x) | Арксинус от x |
| arcsinh(x) | Гиперболический арксинус |
| arctg(x) | Арктангенс от x |
| arctgh(x) | Гиперболический арктангенс |
| asec(x) | Арксеканс от x |
| asech(x) | Гиперболический арксеканс |
| cbrt(x) | Кубический корень из x |
| ceiling(x) | Округление вверх |
| chi(x) | Интегральный гиперболический косинус |
| cos(x) | Косинус от x |
| cosh(x) | Гиперболический косинус |
| cosec(x), csc(x) | Косеканс от x |
| ctg(x) | Котангенс от x |
| diracdelta(x) | Функция Дирака |
| e | Основание натурального логарифма |
| exp(x) | Экспонента (e^x) |
| factorial(x), x! | Факториал |
| floor(x) | Округление вниз |
| gamma(x) | Гамма-функция |
| heaviside(x) | Функция Хевисайда |
| i | Мнимая единица (√-1) |
| lambertw(x) | Функция Ламберта W |
| ln(x), log(x) | Натуральный логарифм |
| log(a,x) | Логарифм по основанию a |
| oo | Бесконечность |
| pi | Число π |
| sec(x) | Секанс от x |
| sech(x) | Гиперболический секанс |
| sign(x) | Знак числа |
| sin(x) | Синус от x |
| sinh(x) | Гиперболический синус |
| sqrt(x) | Квадратный корень |
| sqr(x), x^2 | Квадрат числа |
| Si(x), Ci(x), Shi(x), Chi(x) | Интегральные функции |
| tg(x), tan(x) | Тангенс |
| tgh(x) | Гиперболический тангенс |
| x + y, x - y | Сложение, вычитание |
| x * y, x / y | Умножение, деление |
| x^n, pow(x,n) | Возведение в степень |