Студенты
Изучайте связь между алгеброй и геометрией, углубляйте понимание математических понятий и используйте геометрический калькулятор для выполнения заданий и проектов.
Бесплатный калькулятор геометрии решает геометрические задачи в ясных шагах. Решайте алгебру, калькулюс и геометрию легко! Загрузите фото или введите вопрос для мгновенного ответа.
Геометрический калькулятор — это мощный инструмент, объединяющий функции алгебры, геометрии и анализа данных. Он предназначен для обучения, преподавания и проведения различных геометрических исследований. Онлайн-геометрический калькулятор помогает пользователям интуитивно и эффективно исследовать и решать геометрические задачи.
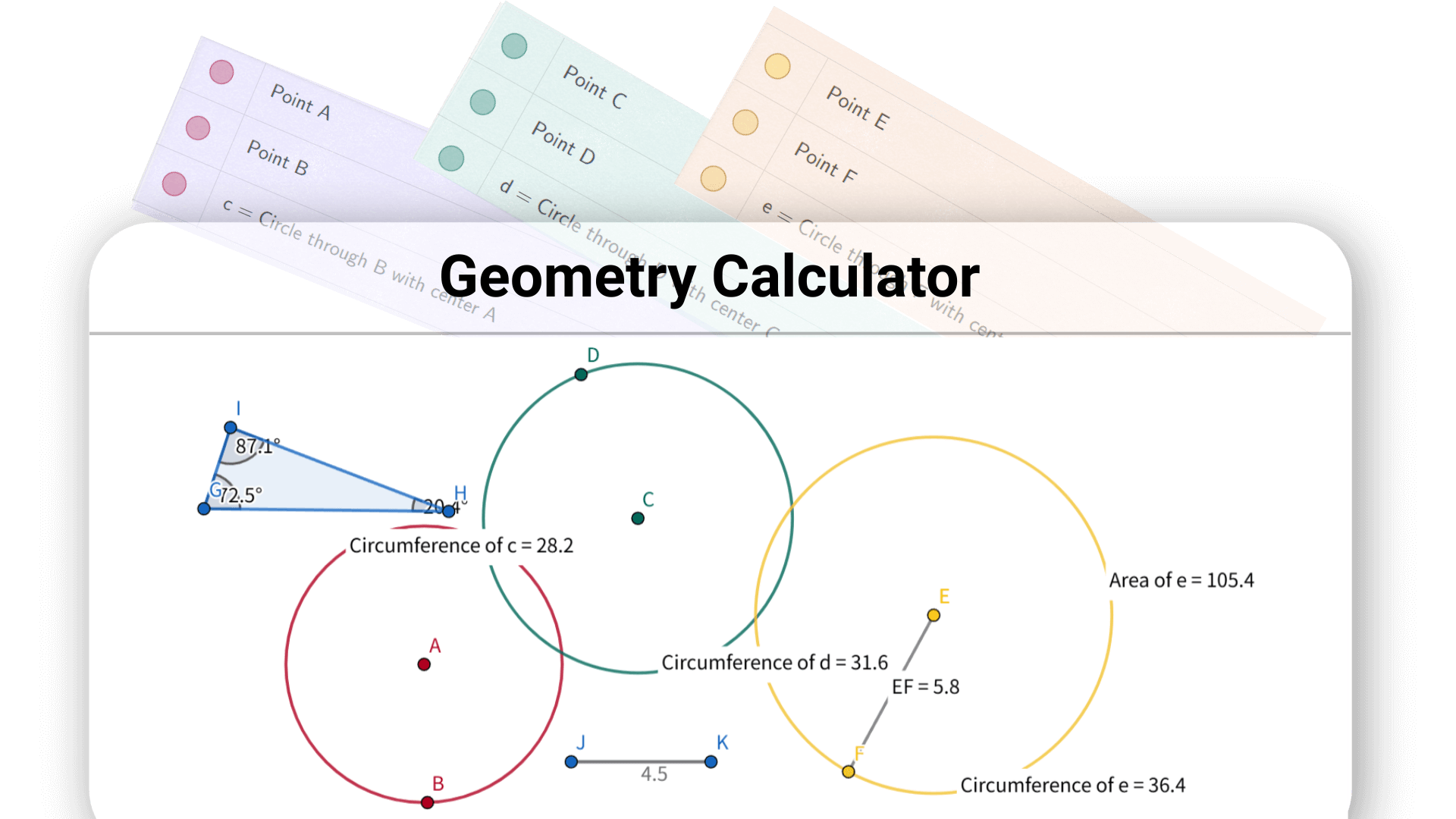
Лучший геометрический калькулятор от Decopy экономит ваше время — больше не нужно листать учебники или рисовать на бумаге. Вы можете сосредоточиться на понимании геометрических концепций, а не тратить силы на сложные вычисления.
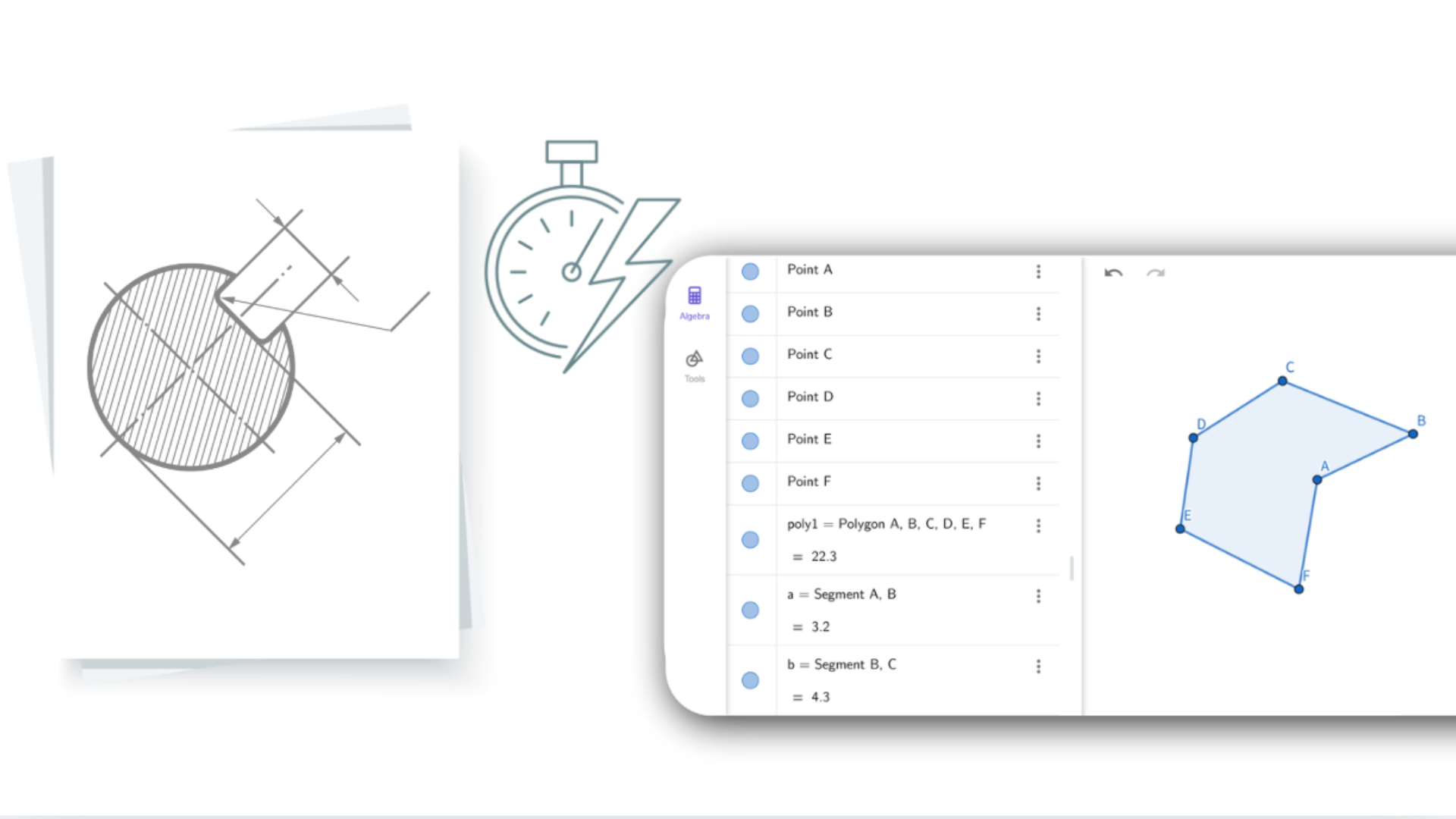
При вводе уравнений или координат геометрический калькулятор мгновенно отображает соответствующие фигуры. Изменение фигуры обновляет связанные алгебраические выражения в реальном времени. Такая динамическая связь объединяет алгебру и геометрию, помогая пользователям рассматривать задачи с разных сторон. Абстрактная математика становится наглядной и легче для понимания.
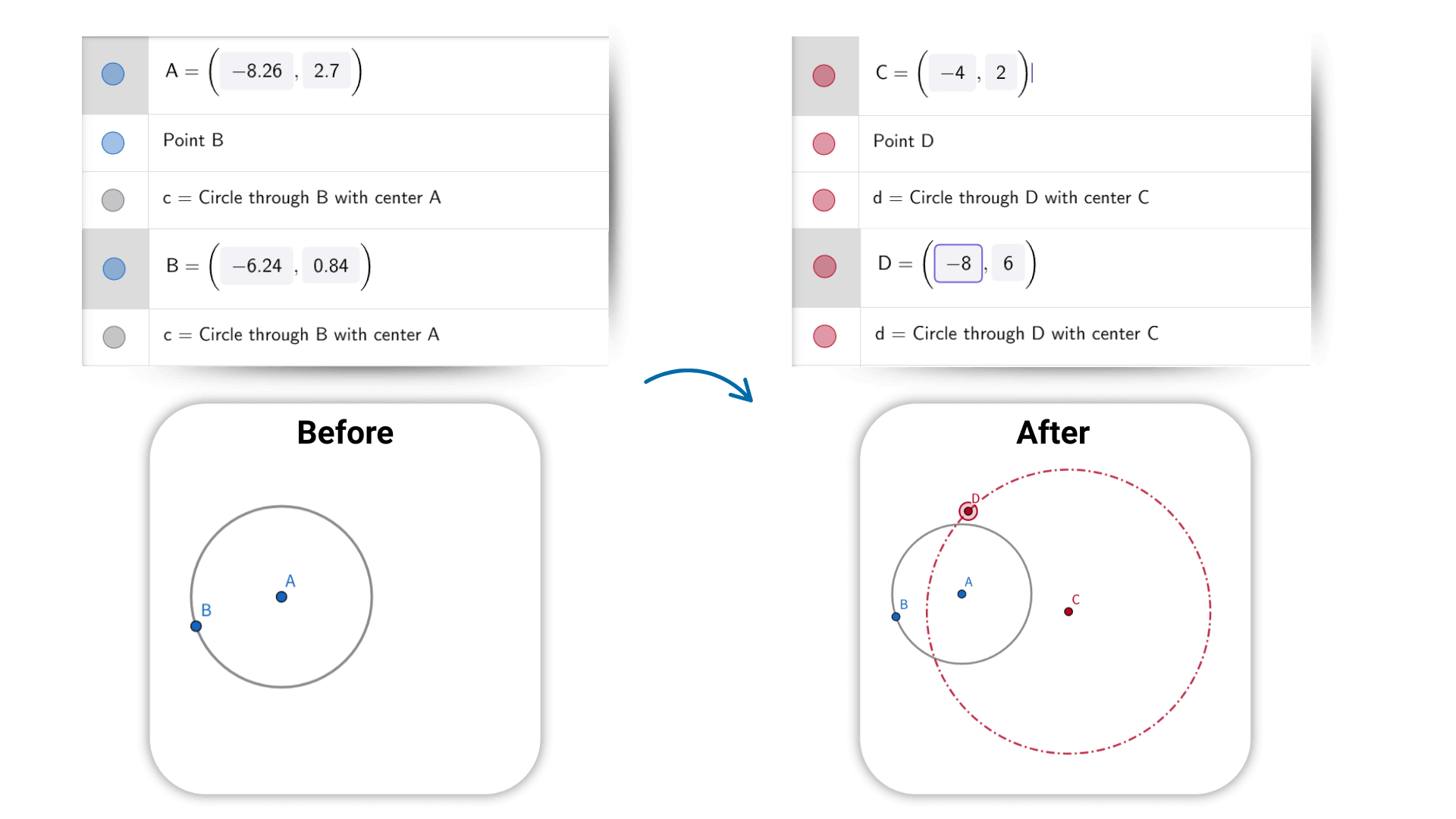
Геометрический калькулятор поддерживает преобразования, такие как перенос, вращение и масштабирование. Простыми действиями вы видите изменения формы в реальном времени. Фигуры, выражения и данные полностью интерактивны: перетаскивание точки или изменение параметра автоматически обновляет связанные отношения и результаты. Этот онлайн-калькулятор помогает исследовать связи и поведение геометрических объектов, облегчая понимание их динамической природы.
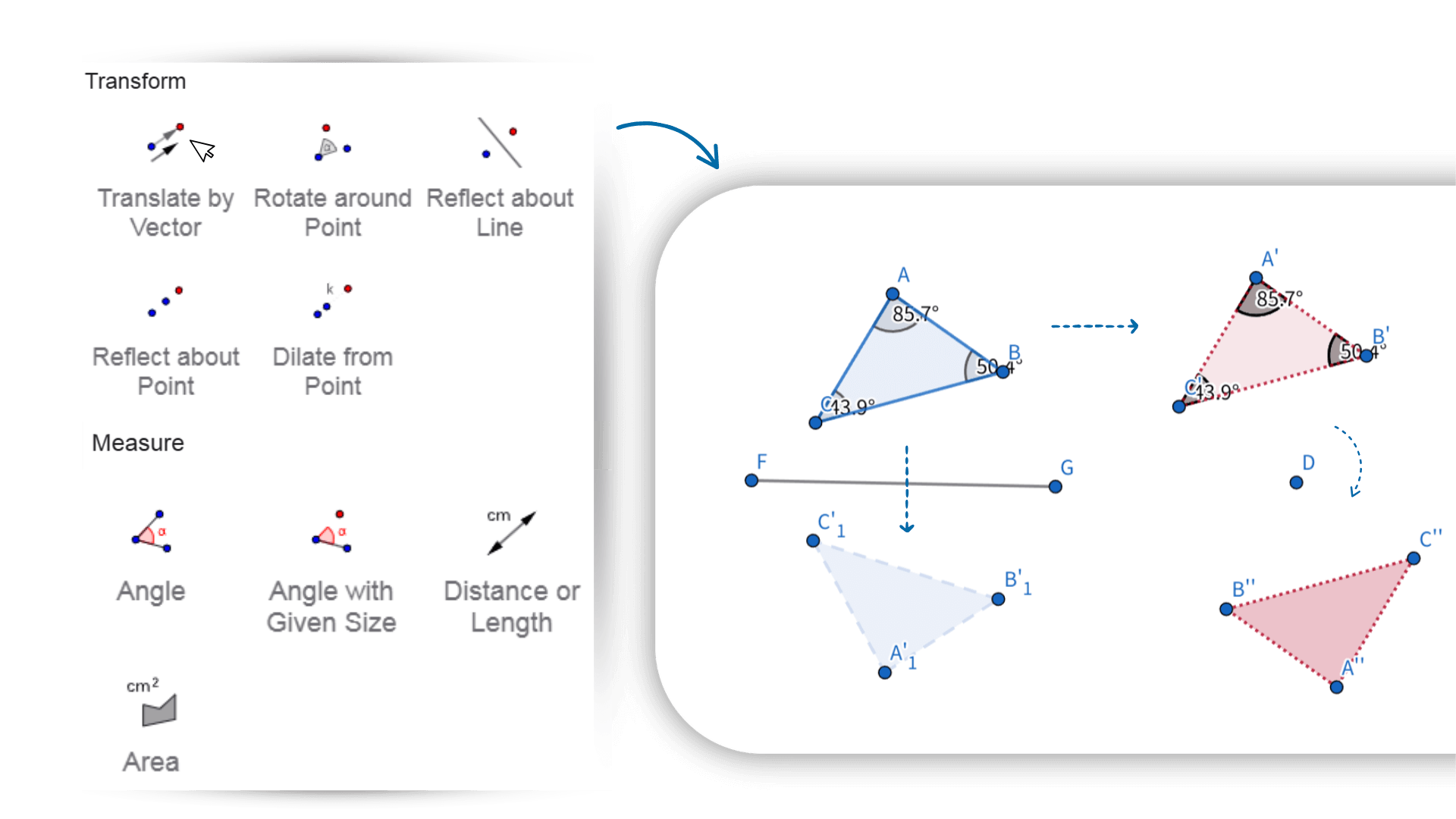
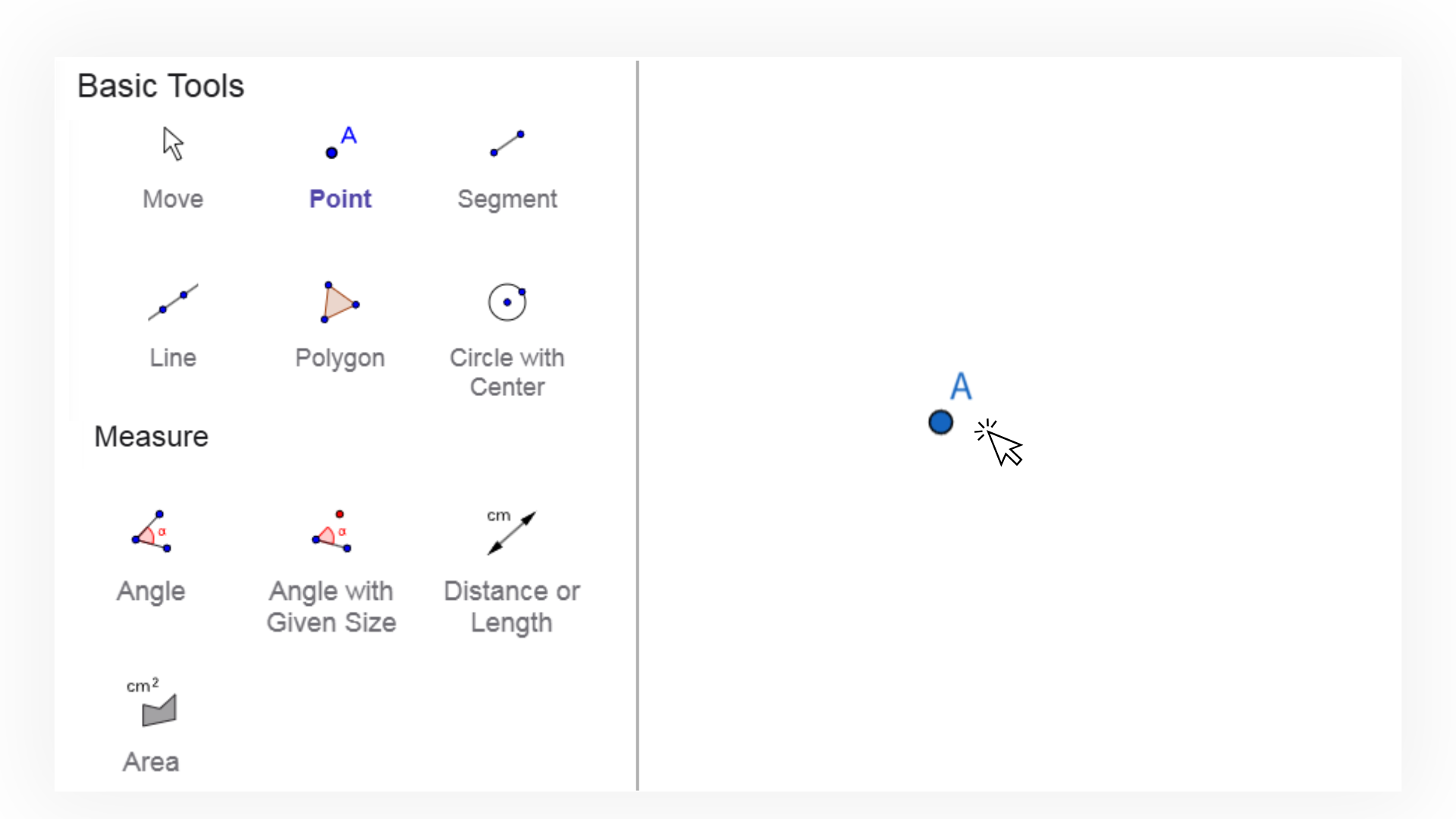
1. ![]() Выберите инструмент «Прямая» и создайте произвольную прямую
AB, дважды кликнув в области построения.
Выберите инструмент «Прямая» и создайте произвольную прямую
AB, дважды кликнув в области построения.
2. ![]() Создайте прямую BC снова с помощью инструмента «Прямая».
Создайте прямую BC снова с помощью инструмента «Прямая».
Подсказка:
Выберите точку B, затем кликните в области построения для
создания точки C.
3. ![]() Активируйте инструмент «Параллельная прямая» и постройте
прямую, параллельную AB, проходящую через точку C.
Активируйте инструмент «Параллельная прямая» и постройте
прямую, параллельную AB, проходящую через точку C.
Подсказка:
Откройте набор специальных прямых, выберите инструмент
«Параллельная прямая», затем выберите прямую AB и точку
C.
4. ![]() Постройте прямую, параллельную BC, проходящую через точку
A, снова используя инструмент «Параллельная прямая».
Постройте прямую, параллельную BC, проходящую через точку
A, снова используя инструмент «Параллельная прямая».
5. ![]() Выберите инструмент «Пересечение» и создайте точку
пересечения D двух прямых.
Выберите инструмент «Пересечение» и создайте точку
пересечения D двух прямых.
Подсказка: Откройте
набор точек, активируйте инструмент «Пересечение» и кликните
непосредственно по точке пересечения.
6. ![]() Активируйте инструмент «Многоугольник» и постройте
параллелограмм ABCD, последовательно выбирая все вершины.
Активируйте инструмент «Многоугольник» и постройте
параллелограмм ABCD, последовательно выбирая все вершины.
Примечание:
Чтобы замкнуть многоугольник, выберите первую точку ещё
раз.
7. ![]() Выберите инструмент «Перемещение» и перетащите вершины
параллелограмма, чтобы проверить правильность
построения.
Выберите инструмент «Перемещение» и перетащите вершины
параллелограмма, чтобы проверить правильность
построения.
1. ![]() Создайте отрезок AB, дважды кликнув в области
построения.
Создайте отрезок AB, дважды кликнув в области
построения.
2. ![]() Постройте окружность с центром в точке B через точку A,
выбрав обе точки в этом порядке.
Постройте окружность с центром в точке B через точку A,
выбрав обе точки в этом порядке.
3. ![]() Перетащите точки A и B, чтобы убедиться, что окружность
связана с ними.
Перетащите точки A и B, чтобы убедиться, что окружность
связана с ними.
4. ![]() Постройте окружность с центром в точке B через точку A,
выбрав обе точки в этом порядке.
Постройте окружность с центром в точке B через точку A,
выбрав обе точки в этом порядке.
5. ![]() Пересеките обе окружности, выбрав их, чтобы получить точку
C.
Пересеките обе окружности, выбрав их, чтобы получить точку
C.
6. ![]() Постройте многоугольник ABC против часовой стрелки. Чтобы
замкнуть многоугольник, выберите первую точку ещё раз.
Постройте многоугольник ABC против часовой стрелки. Чтобы
замкнуть многоугольник, выберите первую точку ещё раз.
7. ![]() Скройте две окружности, активировав инструмент
«Показать/Скрыть объект» и выбрав их. Подтвердите выбор,
выбрав инструмент «Перемещение».
Скройте две окружности, активировав инструмент
«Показать/Скрыть объект» и выбрав их. Подтвердите выбор,
выбрав инструмент «Перемещение».
8. ![]() Покажите внутренние углы треугольника, кликнув внутри
треугольника.
Покажите внутренние углы треугольника, кликнув внутри
треугольника.
Подсказка: Если вы получили внешние углы, вероятно,
вы построили многоугольник по часовой стрелке.
9. ![]() Примените тест перетаскивания, чтобы проверить правильность
построения.
Примените тест перетаскивания, чтобы проверить правильность
построения.
1. ![]() Постройте произвольный треугольник ABC, трижды кликнув в
области построения, затем выберите первую созданную точку
ещё раз.
Постройте произвольный треугольник ABC, трижды кликнув в
области построения, затем выберите первую созданную точку
ещё раз.
2. ![]() Постройте серединный перпендикуляр для каждой стороны
треугольника.
Постройте серединный перпендикуляр для каждой стороны
треугольника.
Подсказка: Инструмент «Серединный
перпендикуляр» можно применить к существующему
отрезку.
3. ![]() Создайте точку пересечения D двух серединных
перпендикуляров.
Создайте точку пересечения D двух серединных
перпендикуляров.
Подсказка: Инструмент
«Пересечение» можно применить к пересечению трёх прямых или
последовательно выбрать две из трёх.
4. ![]() Постройте окружность с центром в точке D через одну из
вершин треугольника ABC, сначала выбрав D, затем одну из
вершин.
Постройте окружность с центром в точке D через одну из
вершин треугольника ABC, сначала выбрав D, затем одну из
вершин.
5. ![]() Выполните тест перетаскивания, перемещая вершины
треугольника, чтобы проверить правильность построения.
Выполните тест перетаскивания, перемещая вершины
треугольника, чтобы проверить правильность построения.
1. ![]() Перед началом построения убедитесь, что изображение жёлтого
цветка сохранено на вашем компьютере.
Перед началом построения убедитесь, что изображение жёлтого
цветка сохранено на вашем компьютере.
2. ![]() Создайте новую точку A.
Создайте новую точку A.
3. ![]() Постройте ось симметрии через две новые точки, дважды
кликнув в области построения.
Постройте ось симметрии через две новые точки, дважды
кликнув в области построения.
4. ![]() Отразите точку A относительно прямой, чтобы получить её
образ A’.
Отразите точку A относительно прямой, чтобы получить её
образ A’.
Подсказка: Сначала выберите точку A,
затем прямую.
5. ![]() Постройте отрезок между точкой A и её образом A’, выбрав
обе точки.
Постройте отрезок между точкой A и её образом A’, выбрав
обе точки.
6. ![]() Включите след для точек A и A′.
Включите след для точек A и A′.
Подсказка:
Щёлкните правой кнопкой мыши (MacOS: Ctrl+клик) по точке и
выберите «Показать след».
Примечание: При
перемещении точки A в области построения будет оставаться
след.
7. ![]() Перетащите точку A, чтобы нарисовать след.
Перетащите точку A, чтобы нарисовать след.
Подсказка:
Пункт меню «Обновить вид» очищает все следы.
1. ![]() Перед началом построения убедитесь, что изображение заката
сохранено на вашем компьютере.
Перед началом построения убедитесь, что изображение заката
сохранено на вашем компьютере.
2. ![]() Вставьте изображение заката в левую часть области
построения с помощью инструмента «Изображение».
Вставьте изображение заката в левую часть области
построения с помощью инструмента «Изображение».
Примечание: Первая и вторая угловые точки A и B
изображения создаются автоматически.
3. ![]() Переместите точку A в нижний левый угол изображения и
посмотрите, как это влияет на картинку.
Переместите точку A в нижний левый угол изображения и
посмотрите, как это влияет на картинку.
4. ![]() Удалите точку B с помощью инструмента «Удаление».
Удалите точку B с помощью инструмента «Удаление».
5. ![]() Создайте новую точку B, введя B = A + (3, 0) в строку
ввода.
Создайте новую точку B, введя B = A + (3, 0) в строку
ввода.
Подсказка: Не забудьте нажать Enter после
ввода.
6. ![]() Установите новую точку B как ВТОРУЮ угловую точку
изображения, чтобы изменить его ширину на 3 см.
Установите новую точку B как ВТОРУЮ угловую точку
изображения, чтобы изменить его ширину на 3 см.
Подсказка: Откройте настройки изображения и выберите
вкладку «Положение».
7. ![]() Постройте вертикальную прямую через две точки в середине
области построения с помощью инструмента «Прямая».
Постройте вертикальную прямую через две точки в середине
области построения с помощью инструмента «Прямая».
8. ![]() Отразите изображение относительно прямой с помощью
инструмента «Отразить относительно прямой», выбрав сначала
изображение, затем прямую.
Отразите изображение относительно прямой с помощью
инструмента «Отразить относительно прямой», выбрав сначала
изображение, затем прямую.
9. ![]() Вы можете уменьшить прозрачность изображения, чтобы лучше
отличать его от оригинала (Настройки изображения, вкладка
«Цвет»).
Вы можете уменьшить прозрачность изображения, чтобы лучше
отличать его от оригинала (Настройки изображения, вкладка
«Цвет»).
1. ![]() Перед началом построения убедитесь, что изображение Барта
Симпсона сохранено на вашем компьютере.
Перед началом построения убедитесь, что изображение Барта
Симпсона сохранено на вашем компьютере.
2. ![]() Выберите инструмент «Изображение», чтобы вставить картинку
Барта.
Выберите инструмент «Изображение», чтобы вставить картинку
Барта.
Подсказка: Геометрический калькулятор
автоматически создаст первую и вторую угловые точки A и B
изображения.
3. ![]() Перетащите первую угловую точку A изображения в позицию (1,
1).
Перетащите первую угловую точку A изображения в позицию (1,
1).
4. ![]() Создайте точку D = (1, 3.9).
Создайте точку D = (1, 3.9).
Подсказка: Вы
можете ввести координаты напрямую в строку ввода.
5. ![]() Установите точку D как ЧЕТВЁРТУЮ угловую точку
изображения.
Установите точку D как ЧЕТВЁРТУЮ угловую точку
изображения.
Подсказка: Откройте настройки
изображения и выберите вкладку «Положение».
6. ![]() Постройте жёсткий треугольник ABD с помощью инструмента
«Жёсткий многоугольник».
Постройте жёсткий треугольник ABD с помощью инструмента
«Жёсткий многоугольник».
Подсказка: Замкните
многоугольник, выбрав первую точку ещё раз. Полученный
многоугольник сохранит форму при перемещении. Его можно
перемещать или вращать, перетаскивая две вершины.
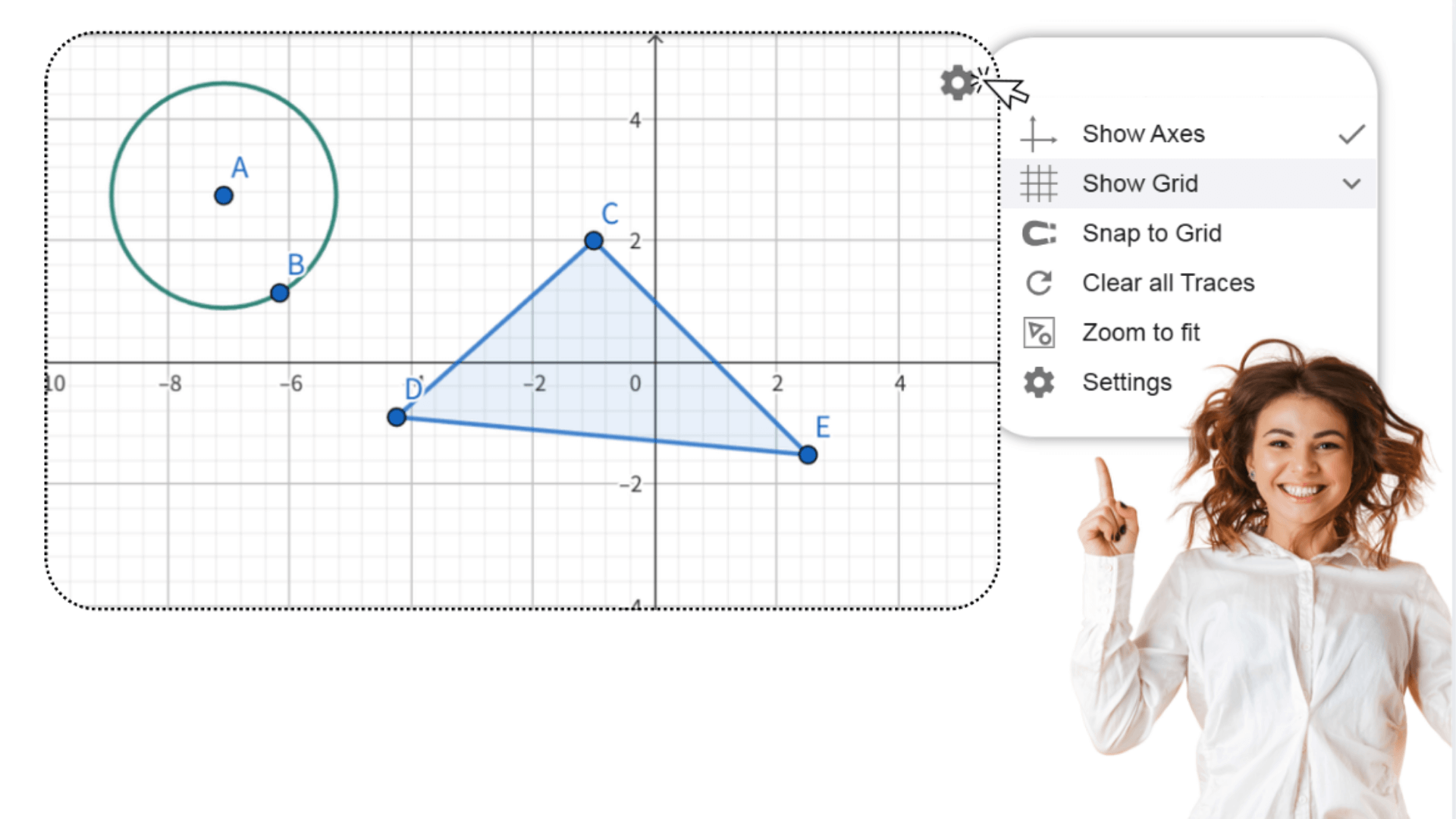
1. ![]() Постройте произвольный треугольник ABC в первой четверти,
разместив вершины на узлах сетки.
Постройте произвольный треугольник ABC в первой четверти,
разместив вершины на узлах сетки.
2. ![]() Создайте новую точку D в начале координат.
Создайте новую точку D в начале координат.
3. ![]() Переименуйте точку D в O.
Переименуйте точку D в O.
Подсказка: Выберите
точку D и просто введите O, чтобы открыть диалог
переименования.
4. ![]() Создайте ползунок для угла α.
Создайте ползунок для угла α.
Подсказка: В окне
ползунка отметьте «Угол» и установите шаг 90°. Убедитесь,
что не удалили символ °.
5. ![]() Используйте инструмент «Вращение вокруг точки», чтобы
повернуть треугольник ABC вокруг точки O на угол α.
Используйте инструмент «Вращение вокруг точки», чтобы
повернуть треугольник ABC вокруг точки O на угол α.
Подсказки:
Активируйте инструмент и выберите треугольник до выбора
центра вращения. В появившемся диалоге введите α с помощью
виртуальной клавиатуры и выберите вращение против часовой
стрелки.
6. ![]() Постройте отрезки AO и A’O.
Постройте отрезки AO и A’O.
7. ![]() Постройте угол AOA’.
Постройте угол AOA’.
Подсказка: Выбирайте
точки против часовой стрелки.
8. ![]() Скройте метку угла AOA’.
Скройте метку угла AOA’.
9. ![]() Перемещайте ползунок и исследуйте образ треугольника.
Перемещайте ползунок и исследуйте образ треугольника.
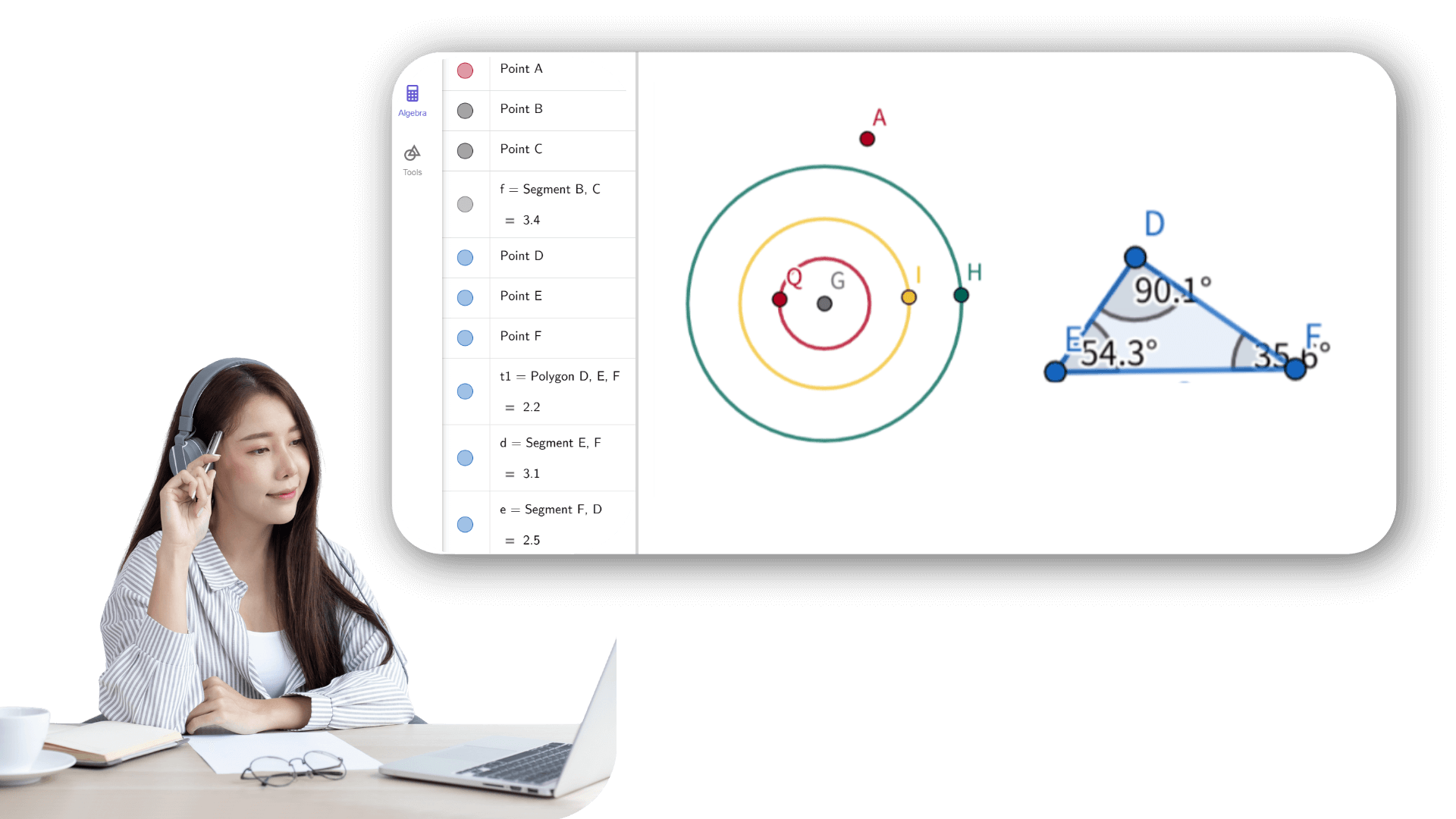
1. ![]() Создайте ползунки a, b и c для длин сторон треугольника с
интервалом от 0 до 10 и шагом 0,5.
Создайте ползунки a, b и c для длин сторон треугольника с
интервалом от 0 до 10 и шагом 0,5.
2. ![]() Установите значения ползунков: a = 8, b = 6.5, c =
10.
Установите значения ползунков: a = 8, b = 6.5, c =
10.
3. ![]() Постройте отрезок f длиной c.
Постройте отрезок f длиной c.
Подсказка: Точки
A и B — концы отрезка.
4. ![]() Постройте окружность d с центром в точке A и радиусом
b.
Постройте окружность d с центром в точке A и радиусом
b.
5. ![]() Постройте окружность e с центром в точке B и радиусом
a.
Постройте окружность e с центром в точке B и радиусом
a.
6. ![]() Постройте точку пересечения C двух окружностей e и f.
Постройте точку пересечения C двух окружностей e и f.
7. ![]() Постройте треугольник ABC.
Постройте треугольник ABC.
8. ![]() Постройте внутренние углы α, β и γ треугольника ABC.
Постройте внутренние углы α, β и γ треугольника ABC.
9. ![]() Постройте точку D на окружности d.
Постройте точку D на окружности d.
10. ![]() Постройте отрезок g между точками A и D.
Постройте отрезок g между точками A и D.
11. ![]() Постройте середину E отрезка g.
Постройте середину E отрезка g.
12. ![]() Введите текст1: b и прикрепите его к точке E.
Введите текст1: b и прикрепите его к точке E.
Подсказка:
После выбора инструмента «Текст» кликните по точке E.
Откройте вкладку «Дополнительно» и выберите b на вкладке
объектов.
13. ![]() Постройте точку F на окружности e.
Постройте точку F на окружности e.
14. ![]() Постройте отрезок h между точками B и F.
Постройте отрезок h между точками B и F.
15. ![]() Постройте середину G отрезка h.
Постройте середину G отрезка h.
16. ![]() Введите текст2: a и прикрепите его к точке G.
Введите текст2: a и прикрепите его к точке G.
17. ![]() Скройте точки D, E, F и G с помощью инструмента
«Показать/Скрыть объект».
Скройте точки D, E, F и G с помощью инструмента
«Показать/Скрыть объект».
18. ![]() Улучшите построение с помощью панели стилей и сопоставьте
цвета соответствующих объектов.
Улучшите построение с помощью панели стилей и сопоставьте
цвета соответствующих объектов.
1. ![]() Постройте треугольник ABC с ориентацией против часовой
стрелки.
Постройте треугольник ABC с ориентацией против часовой
стрелки.
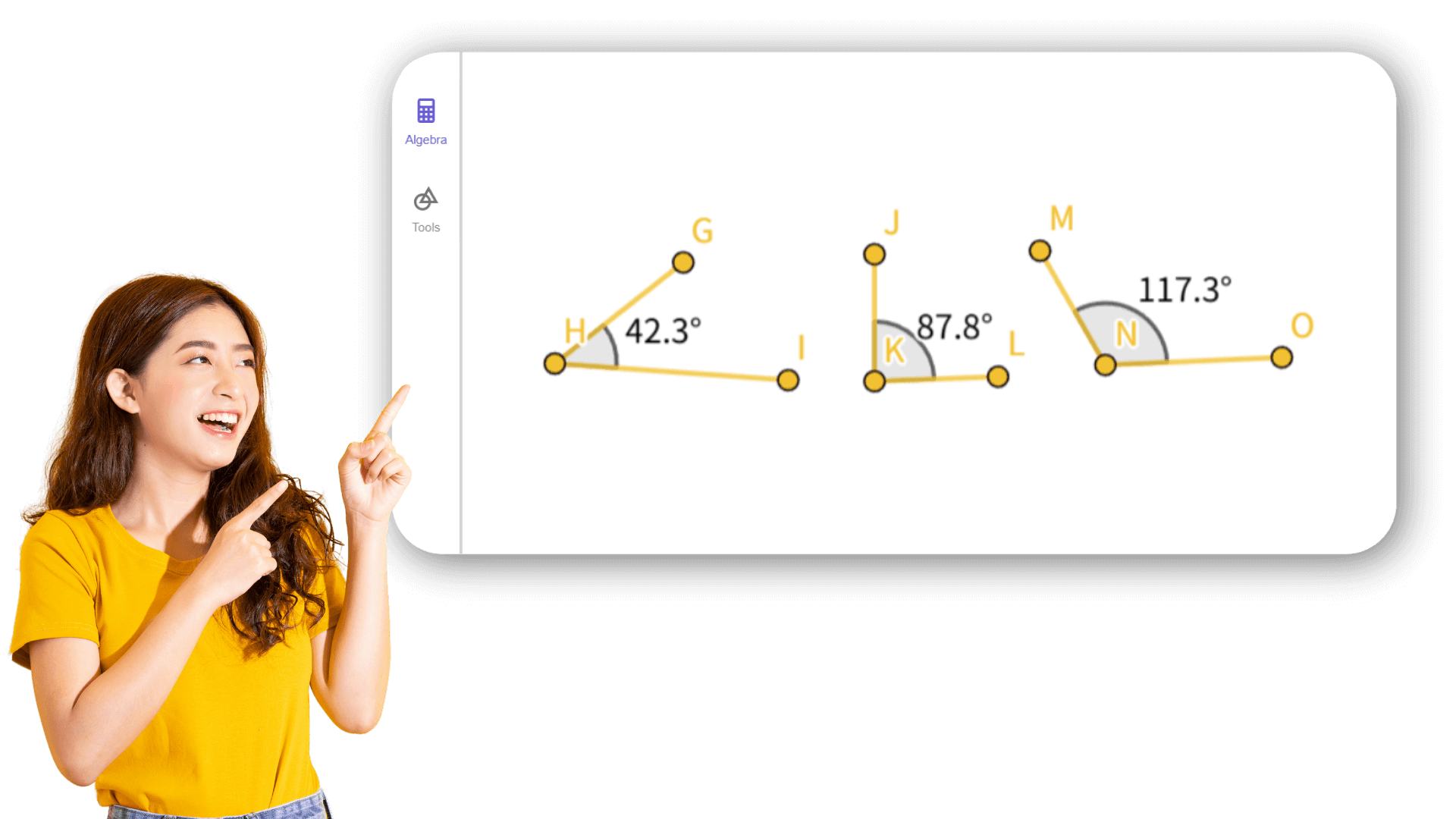
2. ![]() Постройте углы α, β и γ треугольника ABC.
Постройте углы α, β и γ треугольника ABC.
3. ![]() Создайте ползунок для угла δ с интервалом от 0° до 180° и
шагом 10°.
Создайте ползунок для угла δ с интервалом от 0° до 180° и
шагом 10°.
4. ![]() Создайте ползунок для угла ε с интервалом от 0° до 180° и
шагом 10°.
Создайте ползунок для угла ε с интервалом от 0° до 180° и
шагом 10°.
5. ![]() Постройте середину D отрезка AC и середину E отрезка
AB.
Постройте середину D отрезка AC и середину E отрезка
AB.
6. ![]() Поверните треугольник вокруг точки D на угол δ (по часовой
стрелке).
Поверните треугольник вокруг точки D на угол δ (по часовой
стрелке).
Подсказка: Введите δ с помощью
виртуальной клавиатуры.
7. ![]() Поверните треугольник вокруг точки E на угол ε (против
часовой стрелки).
Поверните треугольник вокруг точки E на угол ε (против
часовой стрелки).
Подсказка: Введите ε с помощью
виртуальной клавиатуры.
8. ![]() Передвиньте оба ползунка δ и ε, чтобы получить 180°.
Передвиньте оба ползунка δ и ε, чтобы получить 180°.
9. ![]() Постройте угол ζ, используя точки A’C’B’.
Постройте угол ζ, используя точки A’C’B’.
Подсказка:
Чтобы выбрать правильные вершины, измените угол δ или
используйте команду angle(A’, C’, B’).
10. ![]() Постройте угол η, используя точки C'1B'1A'1.
Постройте угол η, используя точки C'1B'1A'1.
Подсказка:
Чтобы выбрать правильные вершины, измените угол ε или
используйте команду angle(C'1, B'1, A'1).
11. ![]() Улучшите построение с помощью панели стилей.
Улучшите построение с помощью панели стилей.
Подсказка:
Равные углы должны быть одного цвета.
12. ![]() Создайте динамический текст, отображающий внутренние углы и
их значения (например, введите α = и выберите α из списка
объектов на вкладке «Дополнительно»).
Создайте динамический текст, отображающий внутренние углы и
их значения (например, введите α = и выберите α из списка
объектов на вкладке «Дополнительно»).
13. ![]() Вычислите сумму углов, введя
Вычислите сумму углов, введя sum = α + β + γ в
строку ввода.
14. ![]() Вставьте сумму углов как динамический текст:
Вставьте сумму углов как динамический текст:
α + β + γ = и выберите sum из списка объектов
на вкладке.
15. ![]() Сопоставьте цвета соответствующих углов и текста с помощью
панели стилей.
Сопоставьте цвета соответствующих углов и текста с помощью
панели стилей.
16. ![]() Зафиксируйте все тексты, которые не должны перемещаться, с
помощью панели стилей.
Зафиксируйте все тексты, которые не должны перемещаться, с
помощью панели стилей.
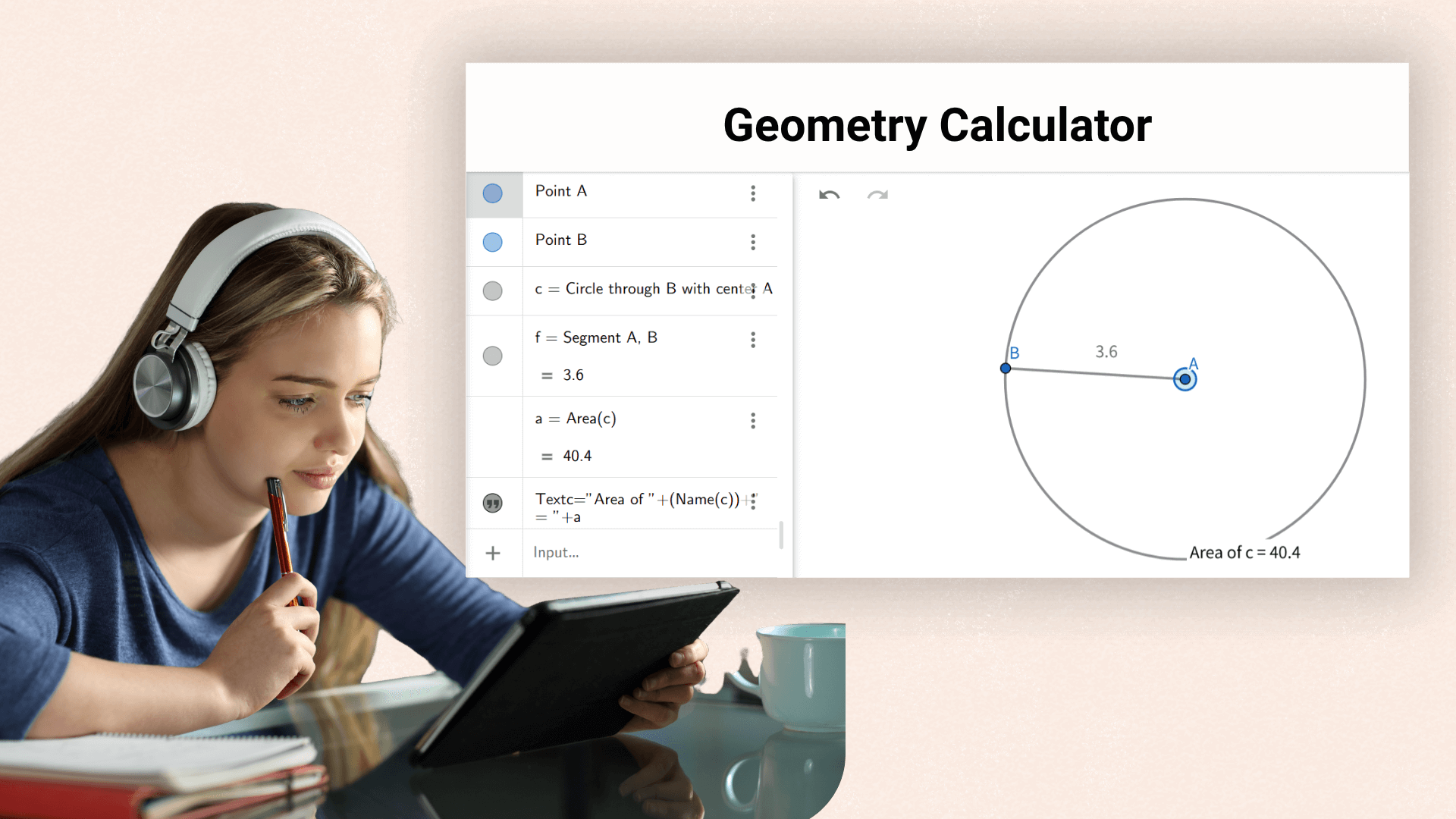
Помогает студентам быстро проверять формулы и решать задачи на занятиях по геометрии, повышая эффективность обучения.
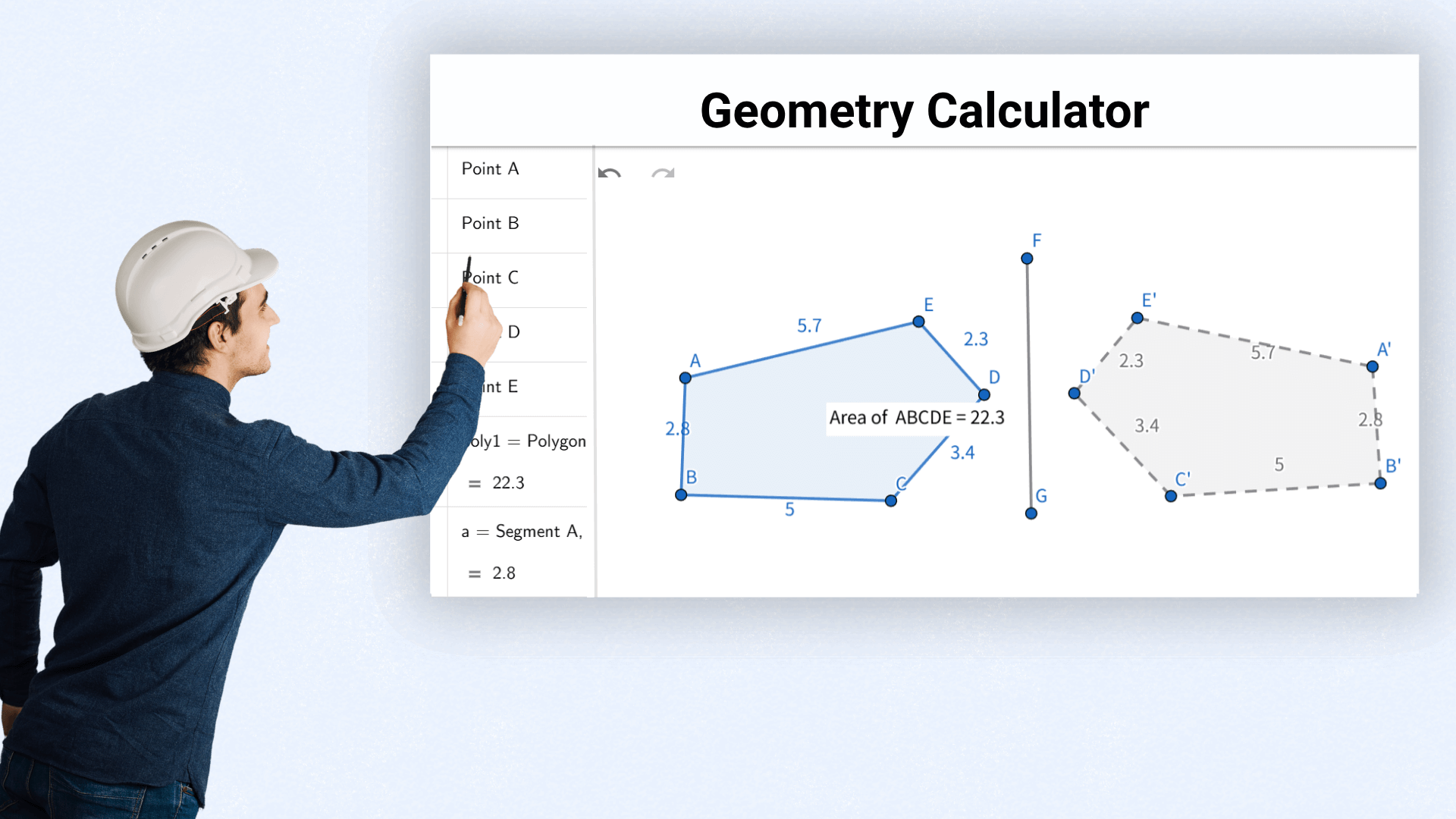
Архитекторы рассчитывают площадь и объем для оценки реализуемости проекта и оптимизации планировки пространства.

Любители используют геометрический калькулятор для точного измерения материалов при создании геометрических поделок.
Изучайте связь между алгеброй и геометрией, углубляйте понимание математических понятий и используйте геометрический калькулятор для выполнения заданий и проектов.
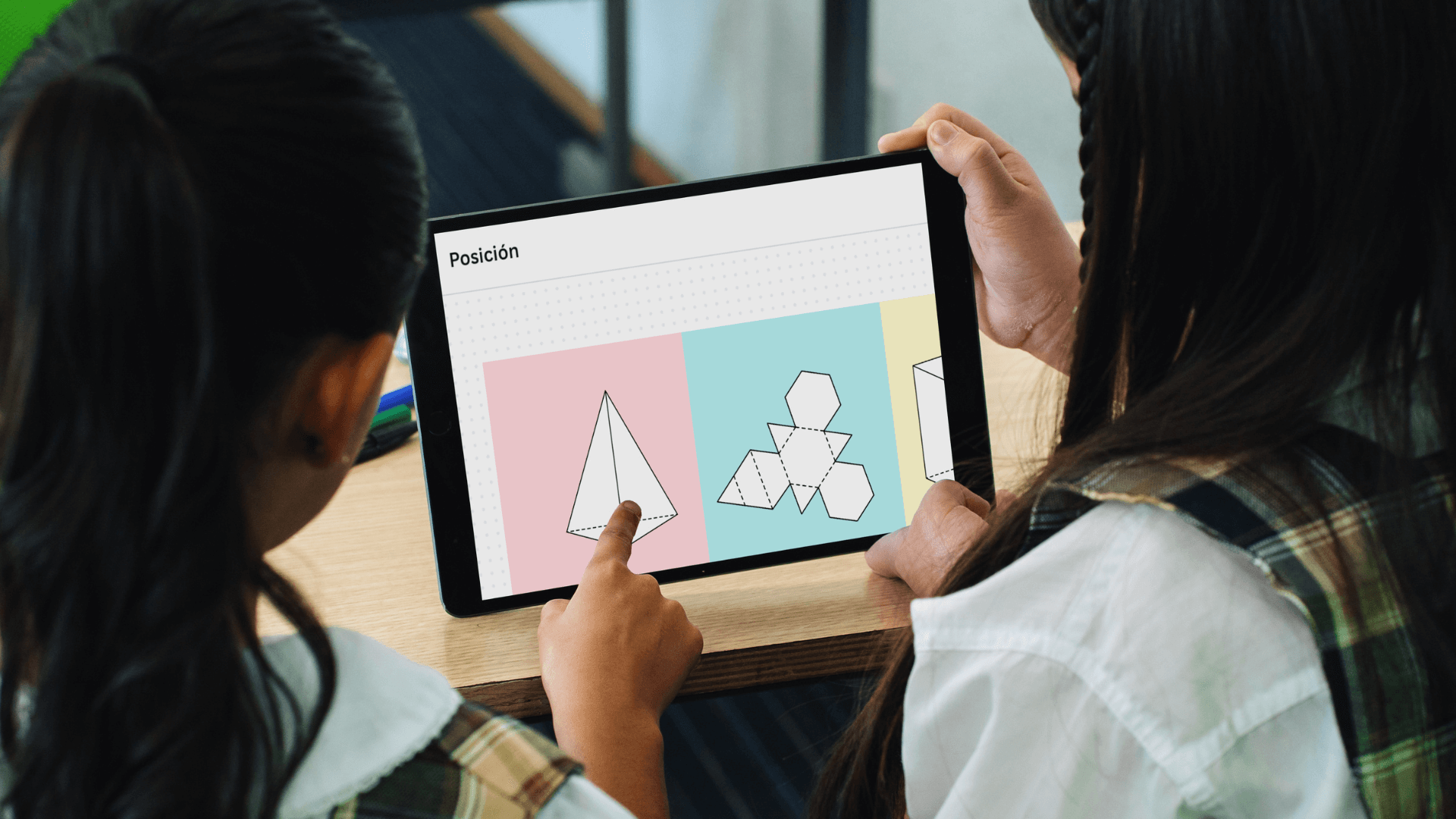
Учителя используют калькулятор для наглядной демонстрации геометрических понятий при подготовке уроков и в классе, повышая эффективность обучения.
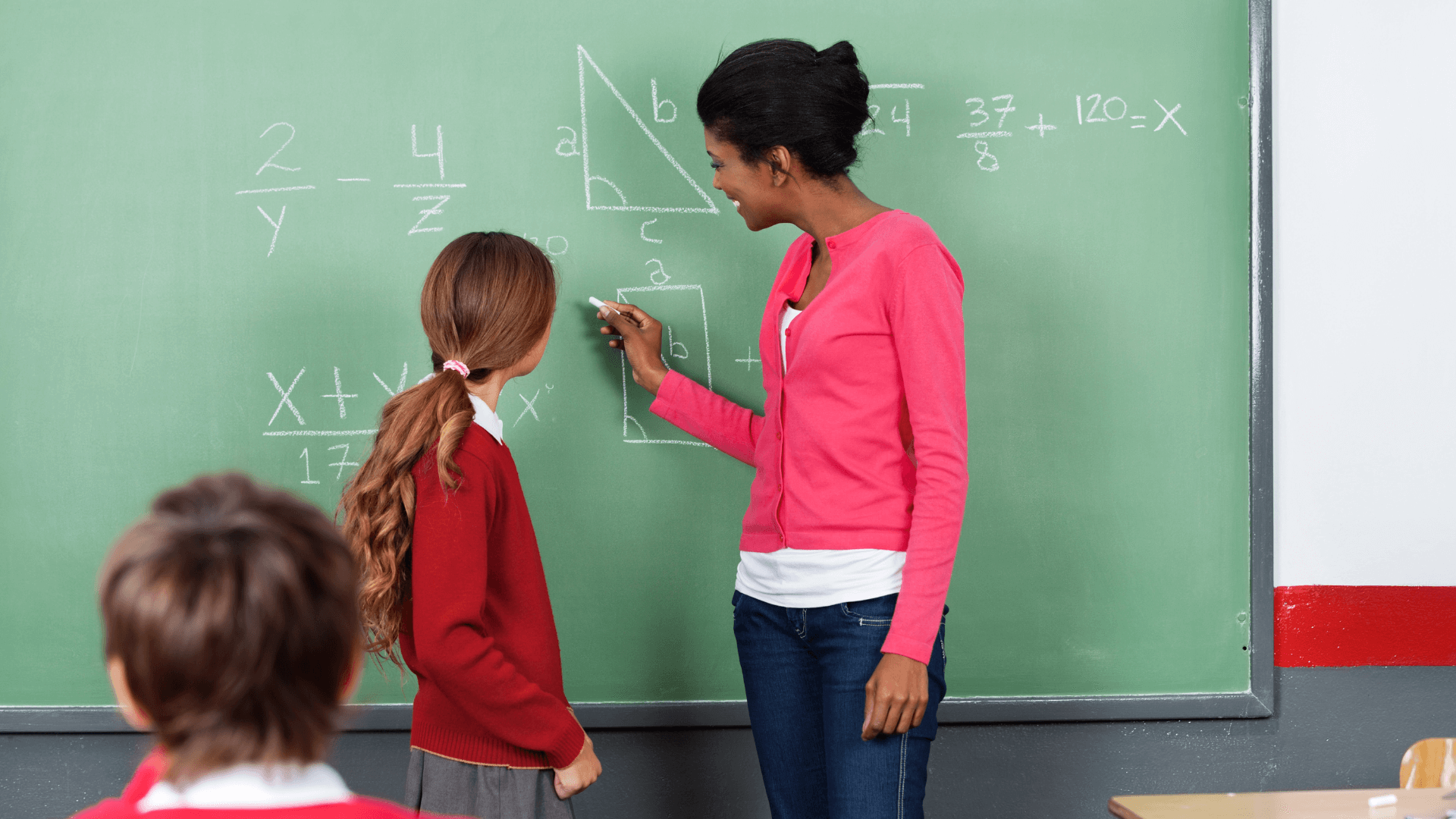
Инженеры используют геометрический калькулятор для точного расчёта углов и длин в конструкциях и механических проектах, снижая ошибки ручных вычислений.

Любители используют калькулятор для точных измерений при создании поделок на основе геометрии.
Используйте геометрический калькулятор для быстрого эскизирования и корректировки ранних концепций, чтобы лучше понять пространственные отношения до перехода к детальным CAD-инструментам.

Исследователи визуализируют сложные структуры и анализируют данные с помощью инструментов рисования и вычислений калькулятора, поддерживая научные исследования.
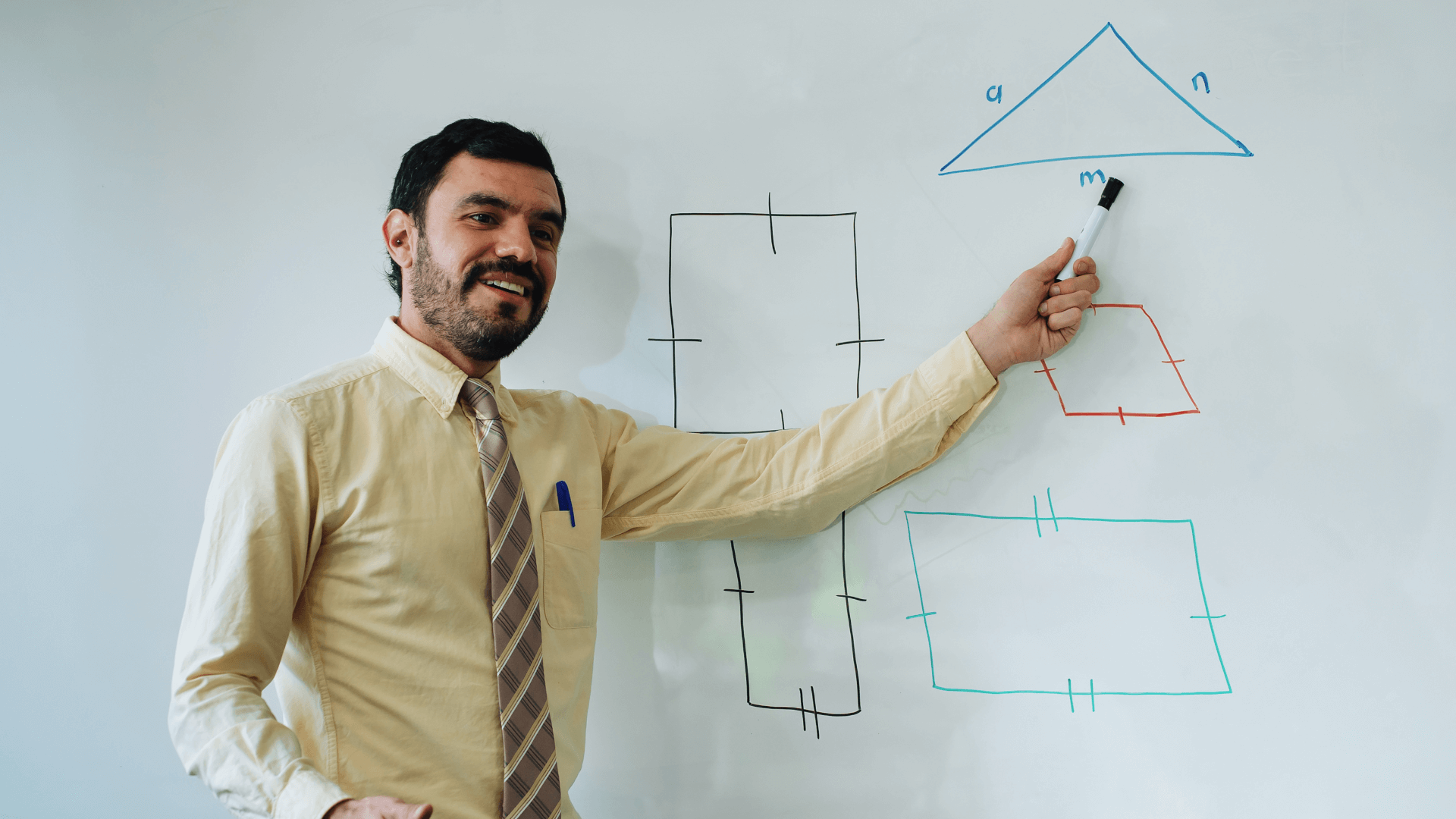
Использует современные алгоритмы для обеспечения высокоточной геометрической обработки.
Простой и интуитивно понятный интерфейс с четкой логикой работы — не требует сложного обучения даже для новых пользователей.
Объединяет множество инструментов и функций для решения различных задач по геометрии в одном месте.
Быстрая работа и плавная обработка даже при больших объемах данных или сложных формулах.
Точное рисование фигур с контролем размеров и свойств, что обеспечивает надежную визуальную основу для анализа и исследований.
Все функции онлайн-калькулятора геометрии доступны без оплаты, что делает качественные инструменты доступными для всех.
Да, он полностью бесплатен. Пользователи могут пользоваться всеми функциями без какой-либо оплаты.
Откройте наш сайт, выберите «Новая геометрия», затем кликните по инструментам, таким как «Точка», «Отрезок» или «Окружность», чтобы разместить фигуры на рабочем поле.
Он широко используется в обучении математике и может помочь при изучении геометрии, алгебры и даже анализа.
Нарисуйте или импортируйте фигуру, выберите объект для измерения, затем выберите свойства, такие как расстояние, длина, угол, периметр или площадь. Результаты появятся на чертеже или в алгебраической области.
Да. Геометрический калькулятор прост в использовании и имеет интуитивно понятный интерфейс — идеально для быстрого старта новичков.
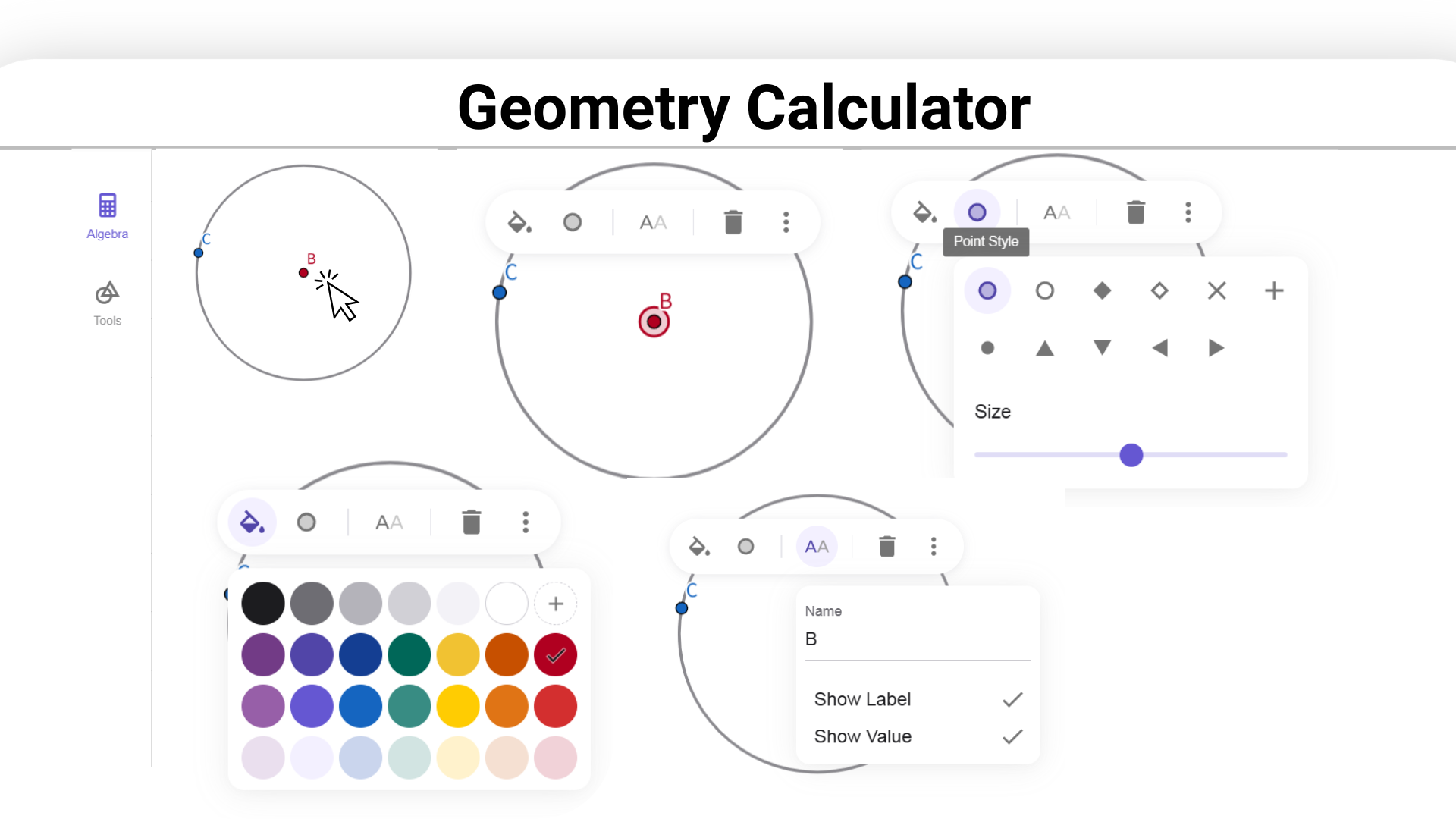
Выберите фигуру и используйте меню правой кнопки мыши или панель свойств, чтобы изменить её внешний вид, включая цвет, стиль линии и заливку.
Наш геометрический калькулятор использует современные алгоритмы для получения точных и надёжных результатов.
Он помогает студентам исследовать связь между алгеброй и геометрией, а также поддерживает их при выполнении заданий и исследовательских проектов более эффективно.