Студенты
Графический калькулятор помогает студентам от начальной школы до университета. Он помогает им понять математические концепции и развивать навыки решения проблем.
Графический калькулятор может решать уравнения и рисовать графики функций, помогая вам интуитивно и точно понимать изменяющиеся модели функций.
Графический калькулятор - это мощный и технологически продвинутый инструмент для рисования графиков функций, выполнения сложных расчетов и анализа данных. Регулируя параметры для влияния на трансформацию графиков, математическое обучение и исследование становятся более интуитивными, эффективными и интересными.
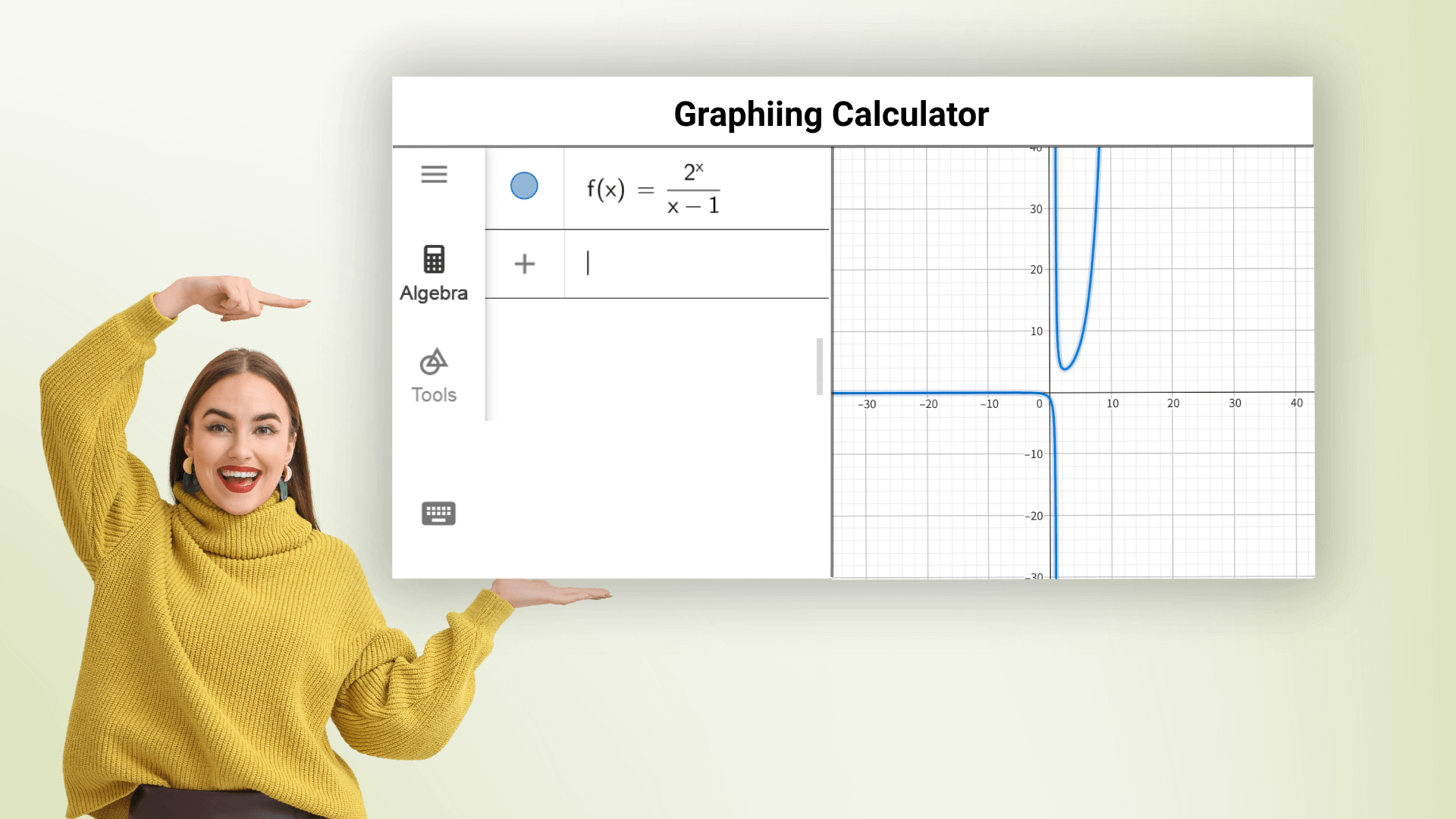
Графический калькулятор может рисовать различные графики функций, включая линейные, параболические, тригонометрические и логарифмические функции, и он может рисовать несколько уравнений одновременно в разных цветах. Просто введите выражение функции, чтобы быстро получить точный график и наблюдать тенденции и характеристики функции. Онлайн-графический калькулятор помогает всем овладевать математикой и избегать сложных расчетов.
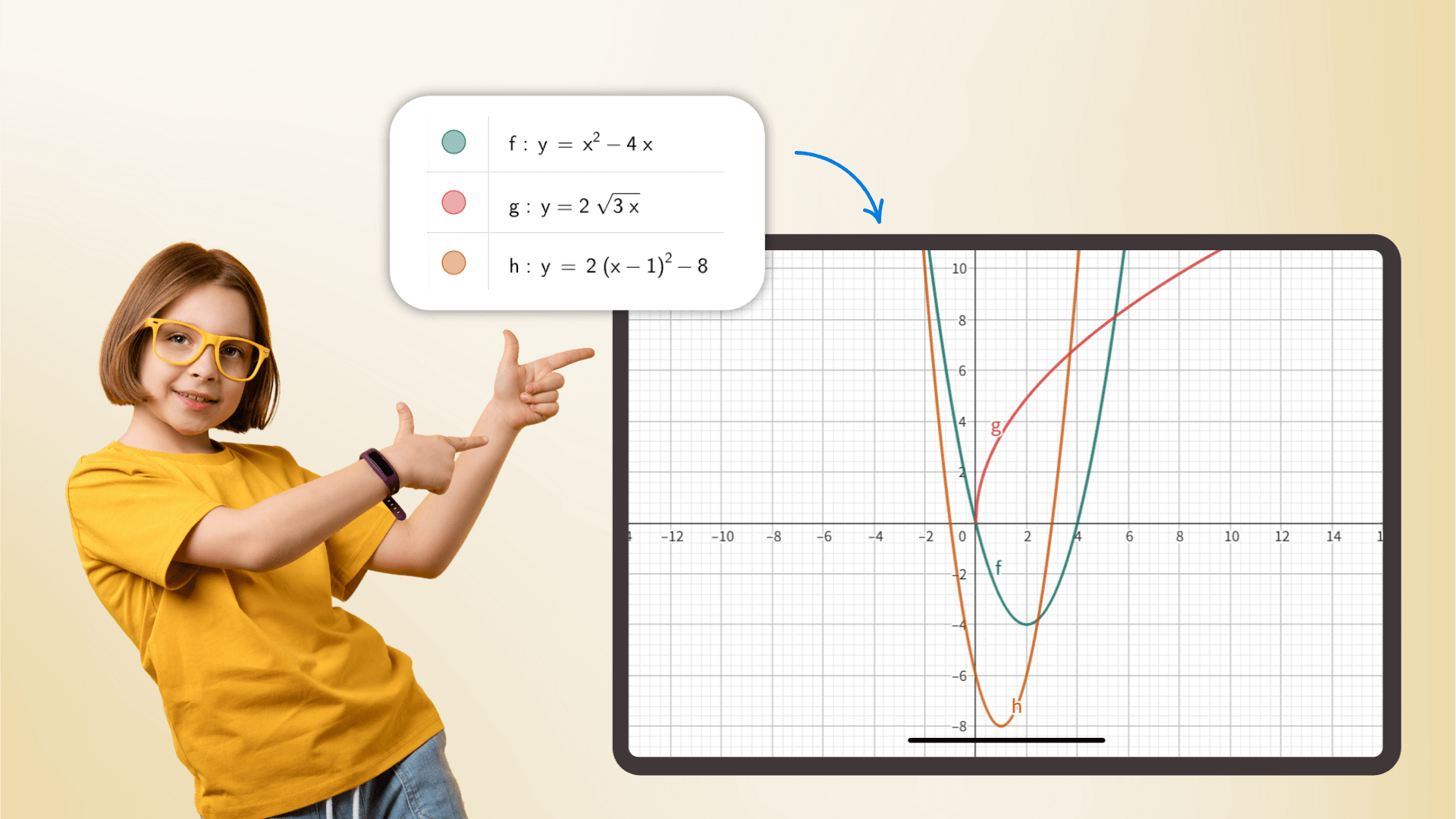
Как научный калькулятор, он обрабатывает все, от базовой арифметики до передовой математики, калькуля, статистики и более того. С точными расчетами, он служит незаменимым помощником для студентов и исследователей, повышая эффективность в академических и профессиональных контекстах.
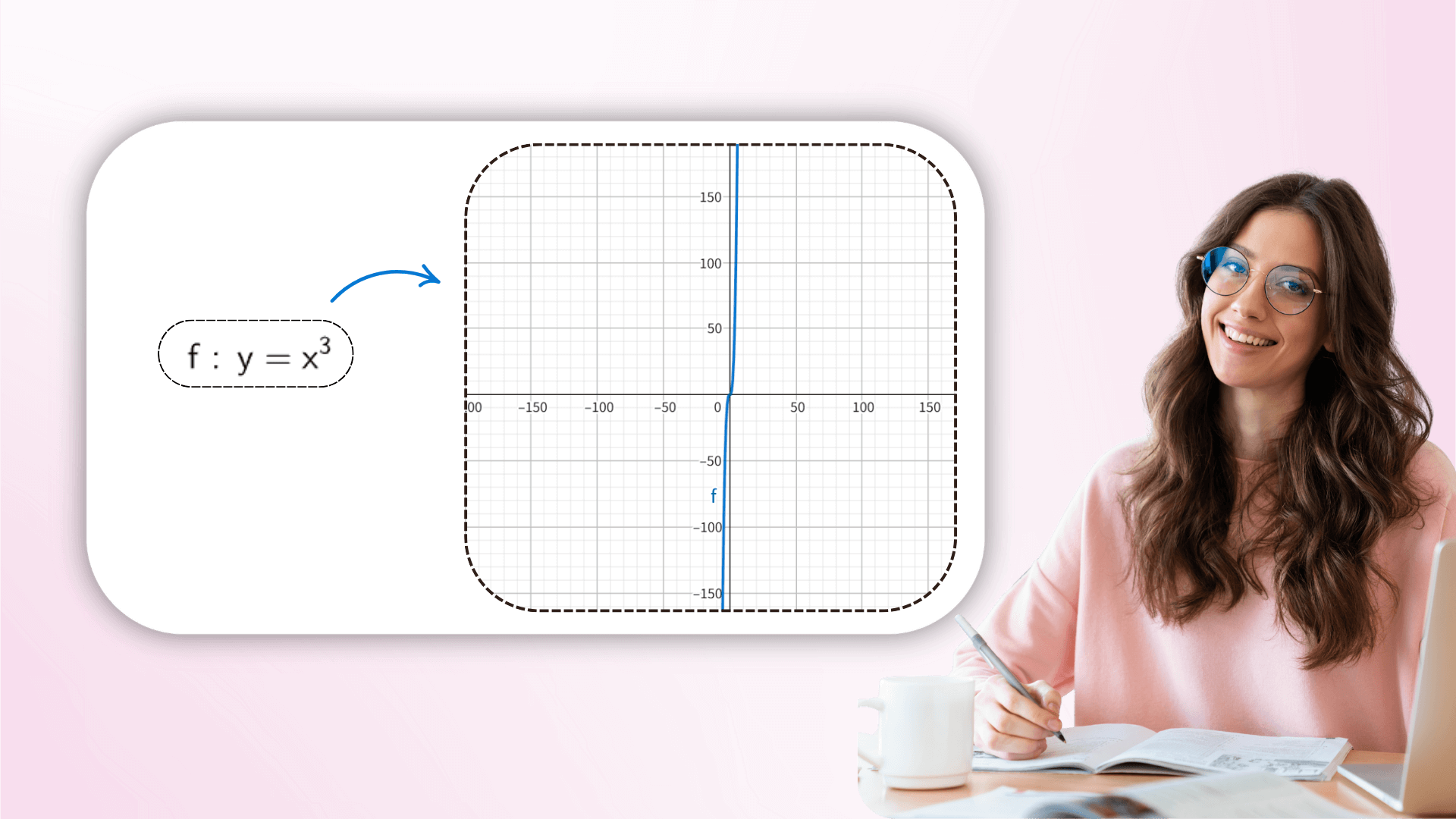
Регулируя значения параметров в реальном времени, пользователи могут наблюдать динамическую трансформацию изображения, чтобы понять, как коэффициенты влияют на геометрию функции, от линейного сдвига до сложных трансформаций, связывая абстрактные формулы с видением. Это интерактивное исследование может углубить понимание математических уравнений.
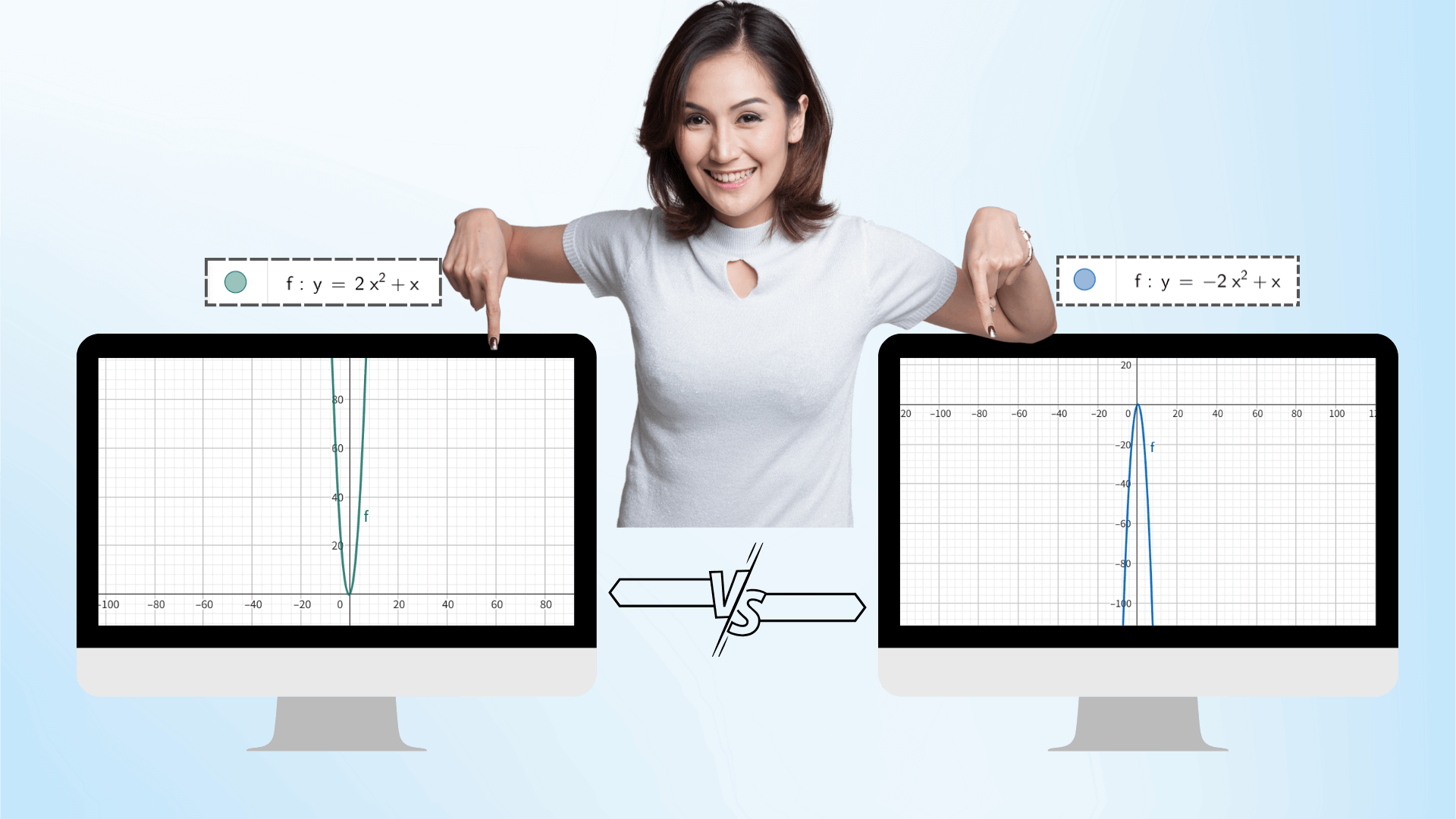
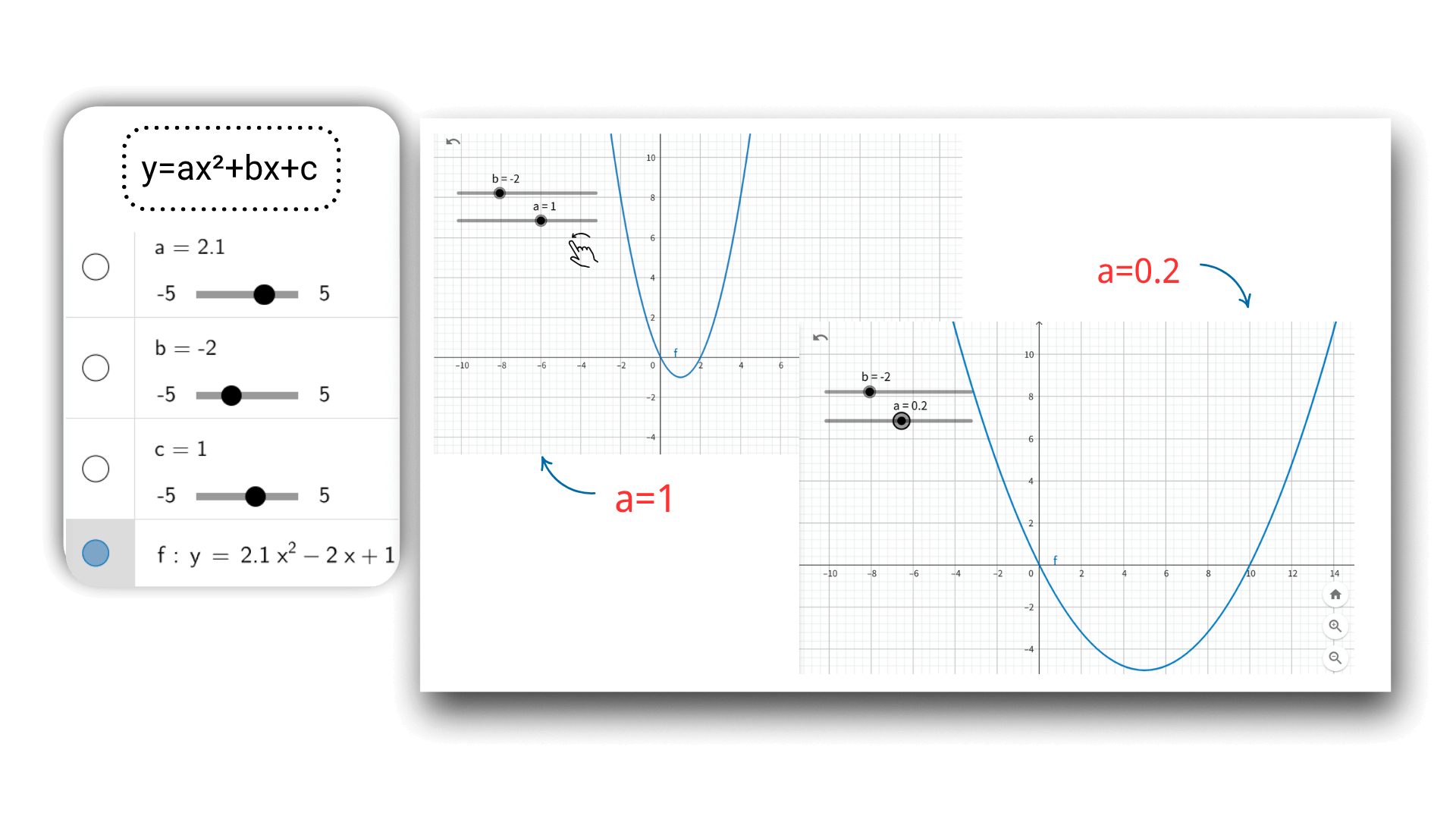
Используя технологию графического рисования с помощью ИИ, после ввода функции вы можете динамически регулировать параметры с помощью ползунка, такие как a, b, c квадратичной функции. Изображение будет деформироваться в реальном времени, как анимация, и данные координат будут обновляться синхронно, интуитивно раскрывая влияние изменений параметров на изображение и лучше понимая связь между математическими понятиями.
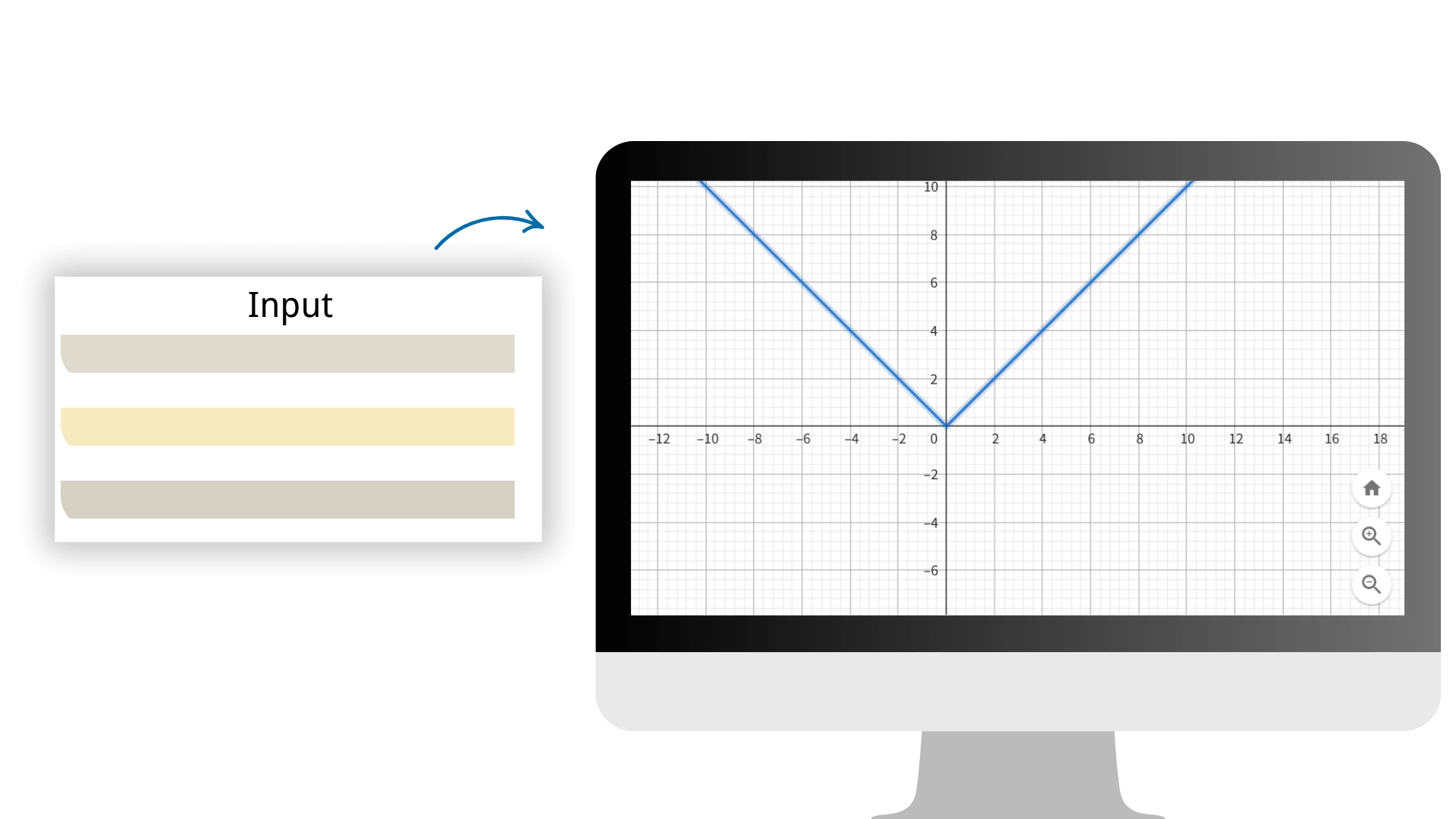
Применяя передовые алгоритмы расчетов, мы обеспечиваем, что каждый результат расчета имеет чрезвычайно высокую точность, обеспечивая надежную поддержку данных для вашей математической работы. Просто введите массив на нашем калькуляторе изображений, чтобы сгенерировать различные изображения одним кликом.
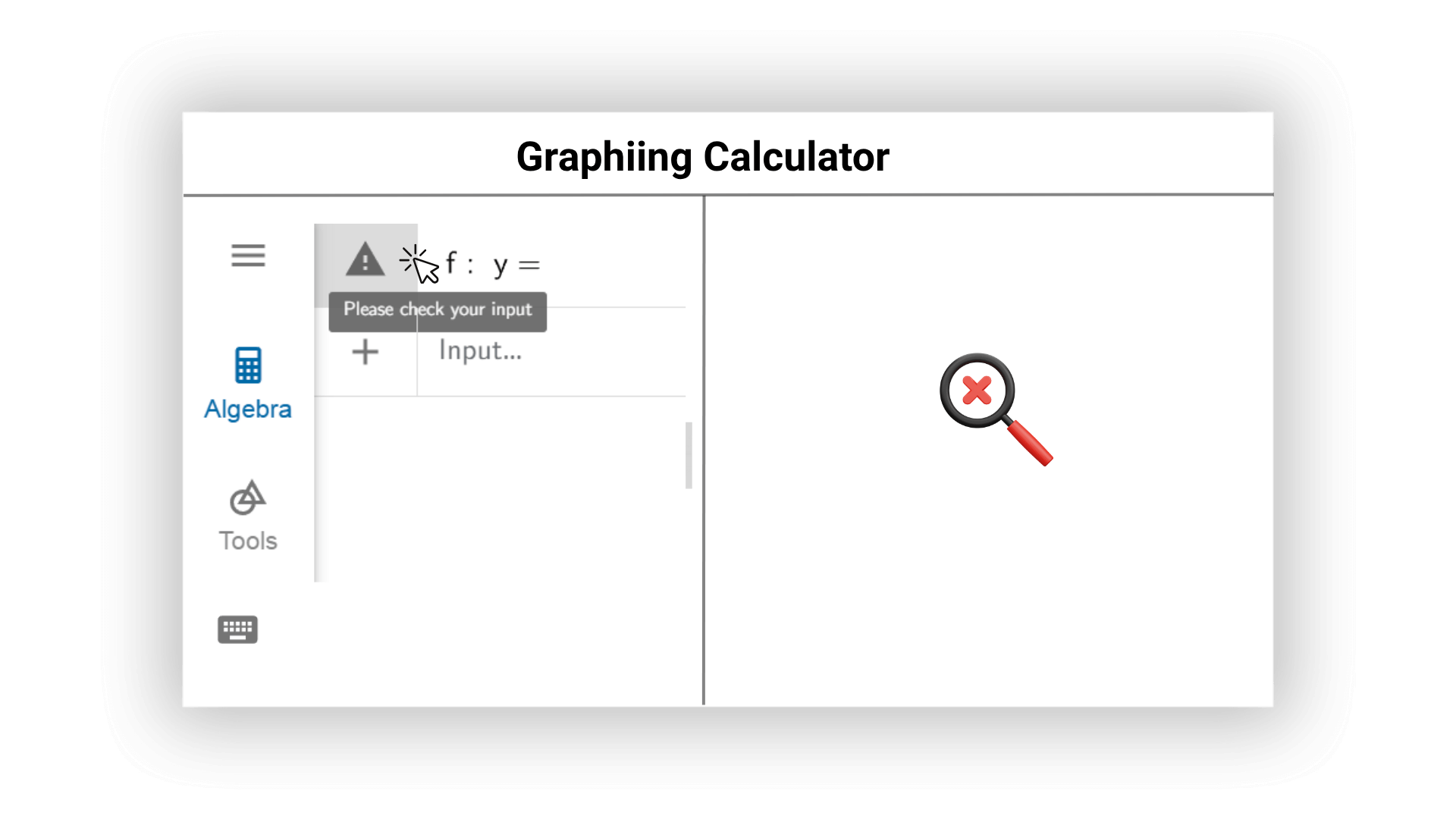
Наш графический калькулятор ИИ может проверять возможные ошибки в математических выражениях в реальном времени и активно предлагать предложения для модификации. ИИ может быстро напомнить пользователям о грамматических проблемах и неразумных вводах, чтобы обеспечить точные результаты расчетов и высокую вычислительную эффективность, и избежать ошибок в изображениях и результатах.
1. ![]() Введите
Введите y = m x + b в панель ввода и нажмите
Enter.
Подсказка: Графический калькулятор
автоматически создаст ползунки для параметров m и b после
нажатия Enter. Чтобы отобразить ползунки в графическом окне,
выберите неактивную кнопку видимости в алгебраическом окне
слева от переменных.
2. ![]() Создайте точку пересечения A между прямой и осью y.
Создайте точку пересечения A между прямой и осью y.
Подсказка:
Вы можете использовать инструмент Пересечение, который
находится в панели инструментов для точек, выбрав два
объекта, или воспользоваться командой Intersect(f,
yAxis).
3. ![]() Создайте точку B в начале координат с помощью инструмента
Пересечение, выбрав две оси.
Создайте точку B в начале координат с помощью инструмента
Пересечение, выбрав две оси.
4. ![]() Выберите инструмент Отрезок в панели инструментов для
прямых и создайте отрезок между точками A и B, выбрав обе
точки.
Выберите инструмент Отрезок в панели инструментов для
прямых и создайте отрезок между точками A и B, выбрав обе
точки.
Подсказка: Также можно воспользоваться
командой Segment(A, B).
5. ![]() Скройте точки A и B, нажав на соответствующие активные
кнопки видимости слева от их координат в алгебраическом
окне.
Скройте точки A и B, нажав на соответствующие активные
кнопки видимости слева от их координат в алгебраическом
окне.
6. ![]() Используйте инструмент Наклон из панели измерений, чтобы
создать наклон (треугольник) прямой, кликнув по
прямой.
Используйте инструмент Наклон из панели измерений, чтобы
создать наклон (треугольник) прямой, кликнув по
прямой.
7. ![]() Улучшите внешний вид вашей конструкции с помощью панели
стилей (например, увеличьте толщину линии отрезка, чтобы он
был виден поверх оси y).
Улучшите внешний вид вашей конструкции с помощью панели
стилей (например, увеличьте толщину линии отрезка, чтобы он
был виден поверх оси y).
1. ![]() Введите f(x) = x^2 в панель ввода и нажмите
Enter.
Введите f(x) = x^2 в панель ввода и нажмите
Enter.
Какой вид имеет график функции?
2. ![]() Используйте инструмент Перемещение и выберите функцию.
Нажмите на панель стилей и выберите опцию снять фиксацию
функции. Теперь вы можете перетаскивать функцию в
графическом окне и наблюдать, как уравнение в алгебраическом
окне изменяется в соответствии с вашими действиями.
Используйте инструмент Перемещение и выберите функцию.
Нажмите на панель стилей и выберите опцию снять фиксацию
функции. Теперь вы можете перетаскивать функцию в
графическом окне и наблюдать, как уравнение в алгебраическом
окне изменяется в соответствии с вашими действиями.
3. ![]() Измените график функции так, чтобы соответствующее
уравнение стало:
Измените график функции так, чтобы соответствующее
уравнение стало:
f(x) = (x + 2)²
f(x) = x² - 3
и
f(x) = (x - 4)² + 2.
4. ![]() Выберите уравнение многочлена. Используйте клавиатуру,
чтобы изменить уравнение на f(x) = 3 x^2.
Выберите уравнение многочлена. Используйте клавиатуру,
чтобы изменить уравнение на f(x) = 3 x^2.
Как
изменится график функции?
5. ![]() Повторите изменение уравнения, вводя различные значения
параметра (например, 0.5, -2, -0.8, 3).
Повторите изменение уравнения, вводя различные значения
параметра (например, 0.5, -2, -0.8, 3).
1. ![]() Введите f(x) = a*x³ + b*x² + c*x + d в панель ввода
и нажмите Enter.
Введите f(x) = a*x³ + b*x² + c*x + d в панель ввода
и нажмите Enter.
Подсказка: Графический калькулятор автоматически
создаст ползунки для параметров a, b, c и d.
2. ![]() Покажите ползунки в графическом окне, выбрав неактивные
кнопки видимости слева от соответствующих записей в
алгебраическом окне.
Покажите ползунки в графическом окне, выбрав неактивные
кнопки видимости слева от соответствующих записей в
алгебраическом окне.
3. ![]() Используйте ползунки в графическом окне, чтобы изменить
значения параметров с помощью инструмента перемещения на
a = 0.2, b = -1.2, c = 0.6, d = 2.
Используйте ползунки в графическом окне, чтобы изменить
значения параметров с помощью инструмента перемещения на
a = 0.2, b = -1.2, c = 0.6, d = 2.
4. ![]() Введите R = Root(f) в панель ввода, чтобы отобразить
корни многочлена. Корни будут автоматически названы R1, R2 и
R3.
Введите R = Root(f) в панель ввода, чтобы отобразить
корни многочлена. Корни будут автоматически названы R1, R2 и
R3.
5. ![]() Введите E = Extremum(f), чтобы отобразить локальные
экстремумы многочлена.
Введите E = Extremum(f), чтобы отобразить локальные
экстремумы многочлена.
6. ![]() Используйте инструмент Касательная, чтобы построить
касательные к многочлену через экстремумы E1 и E2.
Используйте инструмент Касательная, чтобы построить
касательные к многочлену через экстремумы E1 и E2.
Подсказка: Откройте панель специальных линий и
выберите инструмент Касательная. Последовательно выберите
точку E1 и многочлен для построения касательной. Повторите
для точки E2.
7. ![]() Систематически изменяйте значения ползунков с помощью
инструмента перемещения, чтобы исследовать, как параметры
влияют на многочлен.
Систематически изменяйте значения ползунков с помощью
инструмента перемещения, чтобы исследовать, как параметры
влияют на многочлен.
1. ![]() Введите линейное уравнение line_1: y = m_1 x + b_1 в
панель ввода.
Введите линейное уравнение line_1: y = m_1 x + b_1 в
панель ввода.
Подсказка: Ввод line_1 создаёт прямую line1.
2. ![]() Графический калькулятор автоматически создаст ползунки для
переменных m_1 и b_1 после нажатия
Enter.
Графический калькулятор автоматически создаст ползунки для
переменных m_1 и b_1 после нажатия
Enter.
3. ![]() Покажите ползунки в графическом окне, нажав на неактивные
кнопки видимости рядом с их записями в алгебраическом
окне.
Покажите ползунки в графическом окне, нажав на неактивные
кнопки видимости рядом с их записями в алгебраическом
окне.
4. ![]() Повторите шаги 1-3 для уравнения
line_2: y = m_2 x + b_2.
Повторите шаги 1-3 для уравнения
line_2: y = m_2 x + b_2.
5. ![]() Используйте панель стилей, чтобы изменить цвет обеих прямых
и их ползунков.
Используйте панель стилей, чтобы изменить цвет обеих прямых
и их ползунков.
6. ![]() Используйте инструмент Текст и создайте динамический текст,
введя Line 1: в появившемся диалоге и выбрав
line_1 из списка объектов на вкладке Объекты в
разделе Дополнительно.
Используйте инструмент Текст и создайте динамический текст,
введя Line 1: в появившемся диалоге и выбрав
line_1 из списка объектов на вкладке Объекты в
разделе Дополнительно.
7. ![]() Создайте динамический текст со статической частью
Line 2: и выберите line_2 из списка объектов
на вкладке Объекты в разделе Дополнительно.
Создайте динамический текст со статической частью
Line 2: и выберите line_2 из списка объектов
на вкладке Объекты в разделе Дополнительно.
8. ![]() Используйте панель стилей, чтобы цвет текста соответствовал
цвету соответствующих прямых.
Используйте панель стилей, чтобы цвет текста соответствовал
цвету соответствующих прямых.
9. ![]() Постройте точку пересечения A обеих прямых
line_1 и line_2 с помощью инструмента
Пересечение или введя команду
Intersect(line_1, line_2) в панель ввода.
Постройте точку пересечения A обеих прямых
line_1 и line_2 с помощью инструмента
Пересечение или введя команду
Intersect(line_1, line_2) в панель ввода.
10. ![]() Введите xcoordinate = x(A) в панель ввода.
Введите xcoordinate = x(A) в панель ввода.
Подсказка: x(A) возвращает x-координату точки
пересечения A.
11. ![]() Также определите ycoordinate = y(A).
Также определите ycoordinate = y(A).
Подсказка: y(A) возвращает y-координату точки
пересечения A.
12. ![]() Создайте динамический текст со статической частью
Solution: x = и выберите xcoordinate из списка
объектов на вкладке Объекты.
Создайте динамический текст со статической частью
Solution: x = и выберите xcoordinate из списка
объектов на вкладке Объекты.
13. ![]() Создайте динамический текст со статической частью
y = и выберите ycoordinate из списка объектов
на вкладке Объекты.
Создайте динамический текст со статической частью
y = и выберите ycoordinate из списка объектов
на вкладке Объекты.
14. ![]() Зафиксируйте тексты, чтобы их нельзя было случайно
переместить, выбрав тексты и открыв панель стилей.
Зафиксируйте тексты, чтобы их нельзя было случайно
переместить, выбрав тексты и открыв панель стилей.
1. ![]() Введите многочлен f(x) = x^2/2 + 1 в панель
ввода.
Введите многочлен f(x) = x^2/2 + 1 в панель
ввода.
2. ![]() Создайте новую точку A на функции f.
Создайте новую точку A на функции f.
Подсказка: Точка A может перемещаться только
вдоль функции.
3. ![]() Постройте касательную g к функции f через
точку A.
Постройте касательную g к функции f через
точку A.
4. ![]() Найдите наклон касательной g с помощью
m = Slope(g).
Найдите наклон касательной g с помощью
m = Slope(g).
5. ![]() Определите точку S = (x(A), m).
Определите точку S = (x(A), m).
Подсказка: x(A) возвращает x-координату точки
A.
6. ![]() Соедините точки A и S отрезком.
Соедините точки A и S отрезком.
7. ![]() Включите след точки S и перемещайте точку
A.
Включите след точки S и перемещайте точку
A.
Подсказка: Щёлкните правой кнопкой мыши по точке
S (MacOS: Ctrl-клик, планшет: долгое нажатие) и выберите
Показать след.
1. ![]() Введите функцию f(x) = sin(x) в панель ввода.
Введите функцию f(x) = sin(x) в панель ввода.
2. ![]() Щёлкните правой кнопкой мыши по графическому окну и
выберите Графика... . Перейдите на вкладку xAxis и измените
единицу измерения на
Щёлкните правой кнопкой мыши по графическому окну и
выберите Графика... . Перейдите на вкладку xAxis и измените
единицу измерения на π.
3. ![]() Создайте новую точку A на функции f.
Создайте новую точку A на функции f.
Подсказка: Точка A может перемещаться только
вдоль функции.
4. ![]() Постройте касательную g к функции f через
точку A.
Постройте касательную g к функции f через
точку A.
5. ![]() Найдите наклон касательной g с помощью инструмента
Наклон.
Найдите наклон касательной g с помощью инструмента
Наклон.
6. ![]() Определите точку S = (x(A), m).
Определите точку S = (x(A), m).
Подсказка: x(A) возвращает x-координату точки
A.
7. ![]() Соедините точки A и S отрезком.
Соедините точки A и S отрезком.
8. ![]() Включите след точки S и перемещайте точку
A.
Включите след точки S и перемещайте точку
A.
Подсказка: Щёлкните правой кнопкой мыши по точке
S (MacOS: Ctrl-клик, планшет: долгое нажатие) и выберите
Показать след.
9. ![]() Щёлкните правой кнопкой мыши (MacOS: Ctrl-клик, планшет:
долгое нажатие) по точке A и выберите
Анимация в контекстном меню.
Щёлкните правой кнопкой мыши (MacOS: Ctrl-клик, планшет:
долгое нажатие) по точке A и выберите
Анимация в контекстном меню.
Подсказка: В левом нижнем углу графического окна
появится кнопка Анимация. Она позволяет приостанавливать
или продолжать анимацию.
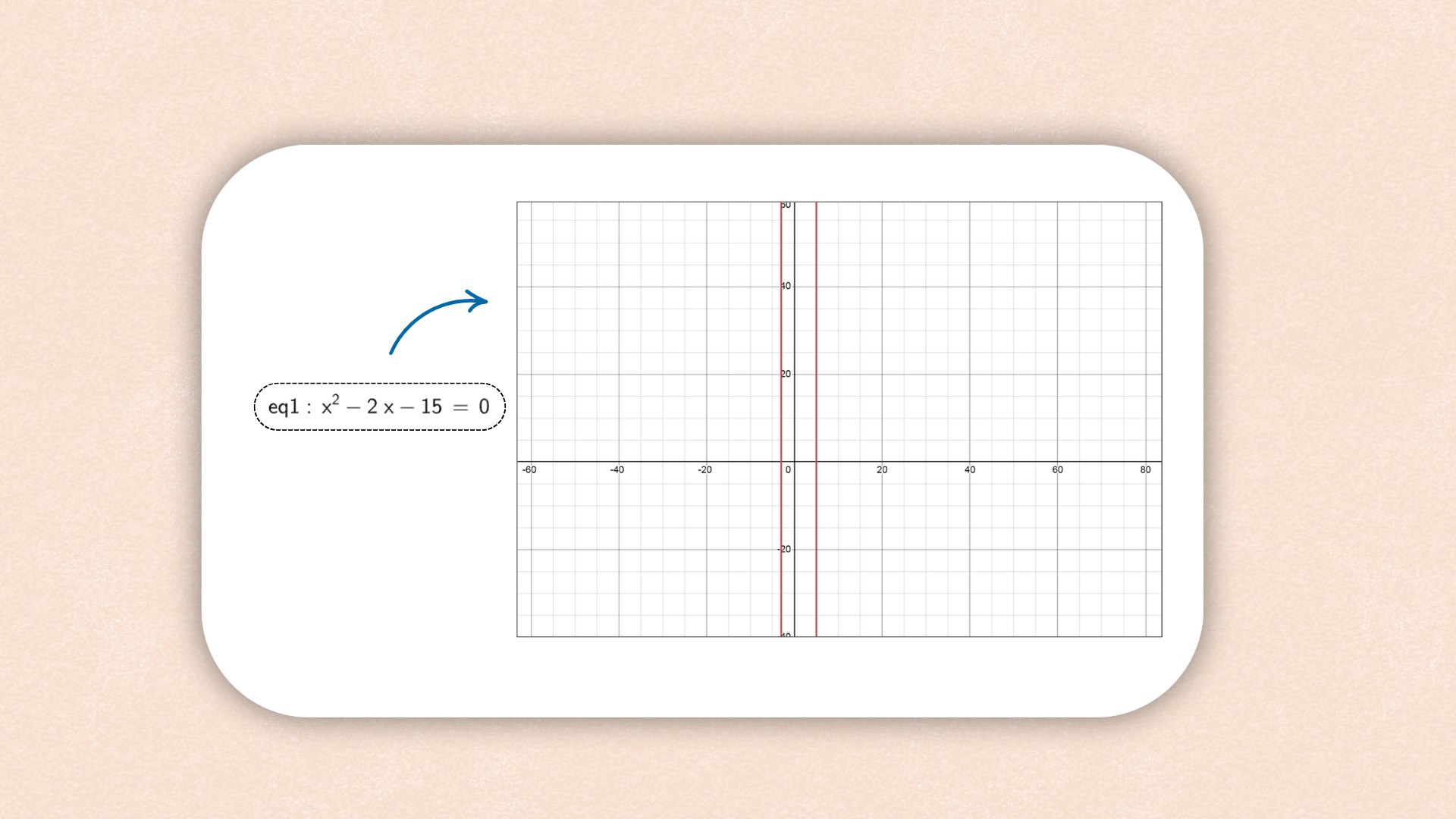
1. ![]() Введите a x + b y ≤ c в панель ввода и нажмите
Enter.
Введите a x + b y ≤ c в панель ввода и нажмите
Enter.
Подсказка: Вы можете использовать
виртуальную клавиатуру для ввода символа ≤. Графический
калькулятор автоматически создаст ползунки для параметров a,
b и c.
2. ![]() Используйте инструмент Перемещение, чтобы установить
значения ползунков a = 1, b = 1 и c = 3.
Используйте инструмент Перемещение, чтобы установить
значения ползунков a = 1, b = 1 и c = 3.
3. ![]() Измените шаг ползунков на 1.
Измените шаг ползунков на 1.
Подсказка:
Выберите число a и откройте панель стилей графического окна.
Откройте настройки числа a и выберите вкладку Ползунок.
Установите шаг равным 1 и повторите для чисел b и c.
4. ![]() Перетащите фон графического окна, чтобы переместить начало
координат в центр.
Перетащите фон графического окна, чтобы переместить начало
координат в центр.
5. ![]() Уменьшите масштаб, чтобы увидеть большую часть координатной
системы на экране.
Уменьшите масштаб, чтобы увидеть большую часть координатной
системы на экране.
6. ![]() Установите расстояние между делениями на осях равным 1.
Установите расстояние между делениями на осях равным 1.
Подсказка:
Убедитесь, что ни один объект не выбран, прежде чем
открывать панель стилей графического окна.
Откройте настройки осей.
Выберите вкладку xAxis и установите расстояние равным 1.
Повторите для вкладки yAxis.
1. ![]() Введите
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) в
панель ввода и нажмите Enter.
Введите
Sequence(Segment((a, 0), (0, a)), a, 1, 10, 0.5) в
панель ввода и нажмите Enter.
2. ![]() Создайте ползунок s для числа с интервалом от 1 до
10 и шагом 1.
Создайте ползунок s для числа с интервалом от 1 до
10 и шагом 1.
3. ![]() Введите Sequence((i, i), i, 0, s) в панель ввода и
нажмите Enter.
Введите Sequence((i, i), i, 0, s) в панель ввода и
нажмите Enter.
4. ![]() Перемещайте ползунок s, чтобы проверить
построение.
Перемещайте ползунок s, чтобы проверить
построение.
1. ![]() Откройте настройки графического окна с помощью панели
стилей.
Откройте настройки графического окна с помощью панели
стилей.
2. ![]() На вкладке xAxis установите расстояние между делениями
равным 1, отметив поле Расстояние и введя 1 в текстовое
поле.
На вкладке xAxis установите расстояние между делениями
равным 1, отметив поле Расстояние и введя 1 в текстовое
поле.
3. ![]() На вкладке Основные установите минимум оси x равным -11, а
максимум — 11.
На вкладке Основные установите минимум оси x равным -11, а
максимум — 11.
4. ![]() На вкладке yAxis снимите галочку Показать ось y и закройте
настройки.
На вкладке yAxis снимите галочку Показать ось y и закройте
настройки.
5. ![]() Создайте два ползунка a и b с интервалом от
-5 до 5 и шагом 1.
Создайте два ползунка a и b с интервалом от
-5 до 5 и шагом 1.
6. ![]() Показывайте значение ползунков вместо их имён с помощью
панели стилей.
Показывайте значение ползунков вместо их имён с помощью
панели стилей.
7. ![]() Создайте точки A = (0, 1) и
B = A + (a, 0).
Создайте точки A = (0, 1) и
B = A + (a, 0).
Подсказка: Расстояние от точки B до точки A
определяется ползунком a.
8. ![]() Создайте вектор u = Vector(A, B) длиной a.
Создайте вектор u = Vector(A, B) длиной a.
9. ![]() Создайте точки C = B + (0, 1) и
D = C + (b, 0).
Создайте точки C = B + (0, 1) и
D = C + (b, 0).
10. ![]() Создайте вектор v = Vector(C, D) длиной b.
Создайте вектор v = Vector(C, D) длиной b.
11. ![]() Создайте точку R = (x(D), 0).
Создайте точку R = (x(D), 0).
Подсказка: Ввод x(D) возвращает x-координату
точки D. Таким образом, точка R показывает результат
сложения на числовой прямой.
12. ![]() Создайте точку Z = (0, 0).
Создайте точку Z = (0, 0).
13. ![]() Создайте три отрезка c = Segment(Z, A),
d = Segment(B, C) и e = Segment(D, R).
Создайте три отрезка c = Segment(Z, A),
d = Segment(B, C) и e = Segment(D, R).
14. ![]() Используйте панель стилей для улучшения вашей конструкции
(например, сопоставьте цвета ползунков и векторов, измените
стиль линий, зафиксируйте ползунки, скройте метки и
точки).
Используйте панель стилей для улучшения вашей конструкции
(например, сопоставьте цвета ползунков и векторов, измените
стиль линий, зафиксируйте ползунки, скройте метки и
точки).
1. ![]() Создайте горизонтальный ползунок с именем
Columns для числа с интервалом от 1 до 10, шагом 1 и
шириной 300.
Создайте горизонтальный ползунок с именем
Columns для числа с интервалом от 1 до 10, шагом 1 и
шириной 300.
Подсказка: Вы можете изменить
ширину ползунка во вкладке Настройки — Ползунок.
2. ![]() Создайте новую точку A.
Создайте новую точку A.
3. ![]() Постройте отрезок f заданной длины Columns,
начиная из точки A.
Постройте отрезок f заданной длины Columns,
начиная из точки A.
4. ![]() Перемещайте ползунок Columns, чтобы наблюдать отрезок с
заданной длиной.
Перемещайте ползунок Columns, чтобы наблюдать отрезок с
заданной длиной.
5. ![]() Постройте перпендикулярную прямую g к отрезку f
через точку A.
Постройте перпендикулярную прямую g к отрезку f
через точку A.
6. ![]() Постройте перпендикулярную прямую h к отрезку f
через точку B.
Постройте перпендикулярную прямую h к отрезку f
через точку B.
7. ![]() Создайте вертикальный ползунок с именем Rows для
числа с интервалом от 1 до 10, шагом 1 и шириной 300.
Создайте вертикальный ползунок с именем Rows для
числа с интервалом от 1 до 10, шагом 1 и шириной 300.
Подсказка:
Вы можете выбрать ориентацию ползунка в диалоге Ползунок на
вкладке Ползунок.
8. ![]() Постройте окружность c с центром в точке A и
радиусом Rows.
Постройте окружность c с центром в точке A и
радиусом Rows.
9. ![]() Перемещайте ползунок Rows, чтобы наблюдать окружность с
заданным радиусом.
Перемещайте ползунок Rows, чтобы наблюдать окружность с
заданным радиусом.
10. ![]() Пересеките окружность c с прямой g, чтобы получить точку
пересечения C.
Пересеките окружность c с прямой g, чтобы получить точку
пересечения C.
Подсказка: При выборе
инструмента Пересечение кликните по точке пересечения над
точкой A, чтобы создать только эту точку.
11. ![]() Постройте параллельную прямую i к отрезку f через
точку пересечения C.
Постройте параллельную прямую i к отрезку f через
точку пересечения C.
12. ![]() Пересеките прямые i и h, чтобы получить точку пересечения
D.
Пересеките прямые i и h, чтобы получить точку пересечения
D.
13. ![]() Постройте многоугольник ABDC.
Постройте многоугольник ABDC.
14. ![]() Скройте все прямые, окружность c и отрезок f.
Скройте все прямые, окружность c и отрезок f.
15. ![]() Скройте метки отрезков с помощью панели стилей.
Скройте метки отрезков с помощью панели стилей.
16. ![]() Установите значения обоих ползунков Columns и Rows равными
10.
Установите значения обоих ползунков Columns и Rows равными
10.
17. ![]() Создайте список вертикальных отрезков с помощью:
Создайте список вертикальных отрезков с помощью:
Sequence(Segment(A + i*(1, 0), C + i*(1, 0)), i, 1,
Columns)
Примечание: A + i*(1, 0) задаёт серию точек, начиная с точки
A, с расстоянием 1 между ними.
C + i*(1, 0) задаёт
серию точек, начиная с точки C, с расстоянием 1 между
ними.
Segment(A + i*(1, 0), C + i*(1, 0)) создаёт
список отрезков между парами этих точек. Обратите внимание,
что концы отрезков не отображаются в графическом окне.
Ползунок
Columns определяет количество создаваемых отрезков.
18. ![]() Создайте список горизонтальных отрезков.
Создайте список горизонтальных отрезков.Sequence(Segment(A + i*(0, 1), B + i*(0, 1)), i, 1,
Rows)
19. ![]() Перемещайте ползунки Columns и Rows, чтобы наблюдать
построение.
Перемещайте ползунки Columns и Rows, чтобы наблюдать
построение.
20. ![]() Вставьте статический и динамический текст, чтобы записать
задачу на умножение, используя значения Columns и Rows как
множители:
Вставьте статический и динамический текст, чтобы записать
задачу на умножение, используя значения Columns и Rows как
множители:text1: Columnstext2: *text3: Rowstext4: =
21. ![]() Вычислите результат умножения:
Вычислите результат умножения:
result = Columns * Rows
22. ![]() Вставьте динамический текст5:
Вставьте динамический текст5: result
23. ![]() Скройте точки A, B, C и D.
Скройте точки A, B, C и D.
24. ![]() Улучшите вашу конструкцию с помощью панели стилей.
Улучшите вашу конструкцию с помощью панели стилей.
Графический калькулятор ИИ - это мощный помощник для студентов, чтобы изучать математику. От средней школы до университета, это алгебра, геометрия, калькулятор или статистика курсов, которые могут помочь студентам лучше понять и овладеть математическими знаниями и улучшить эффективность обучения и оценки. Учителя могут использовать его для проведения демонстраций преподавания и создания живого учебного материала, чтобы стимулировать интерес и энтузиазм студентов в обучении.
Он предоставляет исследователям мощные математические инструменты для облегчения обработки данных, анализа экспериментов, построения моделей и теоретической верификации. В различных научных областях, таких как физика, химия, биология и инженерия, графические калькуляторы могут быть использованы для быстрого и точного выполнения сложных математических операций и анализа данных, помогающих гладкому развитию научных исследований.
Используйте графический калькулятор для рисования кривых спроса и предложения, моделей сложного роста и т.д., анализируйте точку пересечения функций маржинального дохода и затрат, и помочь в принятии бизнес-решений.
Графический калькулятор помогает студентам от начальной школы до университета. Он помогает им понять математические концепции и развивать навыки решения проблем.

Учителя математики могут использовать графический калькулятор для создания материалов для уроков и демонстрации концепций и процессов решения задач, что улучшает эффективность преподавания и взаимодействие.

Исследователи в различных областях полагаются на него для сложных математических расчетов и анализа данных. Графический калькулятор онлайн обеспечивает точные результаты, что ускоряет научные исследования.

Прощайте с утомительной ручной рисовкой, генерируйте профессиональные визуализации данных с одним кликом, рисуйте графики функций онлайн, аннотируйте среднее и дисперсию в реальном времени, динамически подгоняйте кривые регрессии, и эффективно завершайте интеграцию и анализ данных.

Графические калькуляторы помогают программистам визуализировать алгоритмы фильтрации и оптимизировать параметры рендеринга, обеспечивая пиксельно-идеальную производительность функций.

Для архитектурных дизайнеров графические калькуляторы являются мощными инструментами параметрического дизайна, вводите уравнения кривых для генерации графиков функций/смещения, визуально проверяйте механику структур, и сокращайте циклы проектирования.

Все функции не требуют регистрации или оплаты, и вы можете использовать их в любое время.
При расчете сложных задач, таких как определители матриц и интегралы, необходимо поддерживать высокую точность, чтобы избежать ошибок в научных исследованиях.
Расчет выполняется полностью в браузере, данные не загружаются, и страница очищается при закрытии.
Не нужно загружать и устанавливать, мобильные телефоны и компьютеры можно использовать немедленно.
Сосредоточьтесь на сущности обучения, без всплывающих окон и рекламы, и улучшите концентрацию.
Независимо от того, идет ли речь об академических, научно-исследовательских, офисных или инженерных приложениях, мы можем удовлетворить ваши потребности в графических вычислениях.
Вам не нужно регистрироваться или загружать какое-либо программное обеспечение. Просто введите наш сайт в браузер и начните использовать этот мощный инструмент для графика. Вы можете испытать его удобство немедленно.
Да, наш графический калькулятор является полностью бесплатным. Несмотря на то, что он бесплатный, он не ограничивает какие-либо основные функции. Вы можете полностью использовать его функции для графика, расчетов и анализа данных без какой-либо стоимости. Мы стремимся предоставить удобный и эффективный математический инструмент для каждого.
Мы приоритизируем безопасность и конфиденциальность вашей информации. Все ваши расчеты, графики и вводимые данные обрабатываются локально в вашем браузере и никогда не загружаются или не хранятся на наших серверах. Вы можете использовать его с уверенностью, зная, что ваша информация безопасна.
Чтобы ввести функцию, просто введите формулу в поле ввода на домашней странице. Например, введите "y=2x^2" или "f(x)=sin(x)". Калькулятор автоматически обработает ваш ввод и отобразит график.
Да, графический калькулятор может обрабатывать различные функции, от простых линейных уравнений до сложных, таких как интегралы, производные и уравнения с несколькими переменными. Он подходит как для основных, так и для продвинутых математических потребностей, что делает его идеальным для студентов и профессионалов.
Да, он полностью доступен на мобильных устройствах. Вы можете использовать его на смартфонах или планшетах, и он оптимизирован для всех размеров экрана, обеспечивая безшовный опыт где бы вы ни были.