免费方程组计算器 – 在线分步解决数学问题
在线使用免费的方程计算器，轻松求解线性方程、二次方程、三次方程、指数方程、对数方程等各种类型的方程。您可以手动输入方程或上传方程图片，计算器将自动识别并分步骤展示计算结果。它支持多种数学函数和符号，无需登录，快速高效地得到准确的解答。
![\sqrt[x]{y}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIwAAACgCAYAAADeroRzAAAACXBIWXMAABYlAAAWJQFJUiTwAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAATSSURBVHgB7d1daNVmHMfxbIyN9Wa2qwwZkx633XTOdgjqhjuV7tbNrmed4MV0yvCwDXchbAi+rGtB5nBjxU2FTa3vihVFby22CiqCtlV7IeLxBRGxVL2p6I3KP0kxsW3yT+JJPPl+bv59cpJyWprfeZ4nyVPDAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAJLuJcWej4wkeqT4GRDaywag8IqhtPd8MoLm68kESxxIGKjwBwMV/mCgou7DlLqKd6ukkzZ4+YqRKj5HmyQMVEgYS8exTkmWXLbewOhIGKiQMJZt7Vsd7SUtq6S2LW9mwucpJAxU1NeSEjfTG/Ja0sDDIfmBKl8rc2wvDN6WmikfT8I8hYSBSur7MOs3b3K0ZzXOkUqyjIyEgUrq+zDumd2O7k6puU/rSZgRkDBQSW0fpu96QZJlysSMuWHcG1JIlrGRMFBJbcKsbG52tOcvXCC1fe3fhi9JvcfZr4B9PxIGKqkbJQ3P7E5429wweEeKemY3Yb8Pv8KOLkkYqKSuD7Pv8CHzCytZauvrpDKz6w8JA5XUJczGf9c72vkfvjfrkS4D3kgYqKQmYQp3bstwJlMx3txgzex+NftzqXkDfpAwUElNwvza2upoN+S+lFr5ahmjIwUSBirpmel9s9x849b8S9+1gtQp72SCJQwzvYC3ku/DbNi/RyIgn5sr7cxHNVIDJ0vKkTBQKfmE2b1jp6O9cPF3Ulcs/tGAHgkDlZIdJT0zs2sZeDAkNfT8C6MkwFvJ9mH++medo92waIFUZnbDIWGgUrIrgbufaOw+3ys1+0FNNAlDHwbw5r8P84Ks6e9eq25c1USpkSVLypEwUCm5UZJ7rbpvFn0rtW15s4HwSBiolMznetHXqmOUBHiLvA9jn+ktf6yRdjabldrf3y/1yVXi55JqrFVXHCQMVCI7++xkmTpturSv9p5z7lBRLqVw6aLUqM/8oq9VRx8G8Ba6D2Mny7SPP5H2cLKUvW7Woftmte7Wb2xqMqLEWnXFRcJAJXDCuJPl8pkeqfZd+dt2bJc6s/pDx3FnjxyV2rJxnRwfdtQUeq06qJAwUFGf3V7JcvrkCan2nW1LWlfJ/m0rXNdyrFHTwM0bjv217yP0WnVBMUoCvKn7MF2nTkr1Shbbyp9/kbr1/81S7165Zr5gJULTvHlGEKxVFw8SBiqBz0b7zra66TOk7dUH6b7QK/tnJ9eM/P2UM7OTptbK97OTbkPHHqn5xrnFSRj6MIC3on/ez1/6k5yS7X+65kl8jppGW6tu4NbNMY+LHAkDeCv6Pb1rV6+W2r5pi7nh7j2zWqOdpcuWjXk8a9XFi4SBSmxnpfv5IbdRn1SMeq26oOjDAN5iey7Jnm+ZlZsjp+jR/Qcdrzd8Yd6Ta18zsmd2WasuXiQMVGJ/8nHfrl1SK9+aYG6wRk32vbm/rfldat/ZHsdxrFUXDxIGKon5/B++Ay/vLzEiW6suKEZJgLfEjTBqP6uTU7ans2vE1+216g78tyXe987/rQa8JS5hhq9GT3rP3GBfa7IcPnFc6uwZM5l/iQEJA5XEnqX2qKm6ulra71eZTzYysxsvEgYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMCnx7casgoVoq9MAAAAAElFTkSuQmCC)
![\text{[x]}](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIwAAACgCAYAAADeroRzAAAACXBIWXMAABYlAAAWJQFJUiTwAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAGXSURBVHgB7d09ThtRAEbRB6FLUiVNlD5VSsRSWCQ7QaKkYguYJYCRDBUF6PIzzMPnSNY0lmWNrz49VzMGAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAwk4OxlIOxHa+xXfA7rtHK7tvhgGC1wXz/+2f32ns/fzy8VsLCkHzeGWbfzybvbaH7a2FIjsasXvvvYa0mWVwLQzLvwjw6u5x7aE7/z3WUszAkgiERDIlgSARDIhgSwZAIhkQwJIIhEQyJYEgEQyIYEsGQCIZEMCSCIREMiWBIBEMiGBLBkAiGRDAkgiERDIlgSARDIhgSwZAIhkQwJIIhEQyJYEgEQyIYEsGQCIZEMCSCIREMiWBIBEMiGBLBkAiGRDAkgiERDIlgSARDIhgSwZAs99Dkp0+yf+uT4J9+3uze+35sP+a3tTAkR2NW2zHXI+W/CAtD8nkL88IZ5N/J8e56dX6x30uysrOahSFZfmEOHxu9u3v2bZvNZtB9+/1rd729vhkfwcIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB8YfdjnSIL80RMvQAAAABJRU5ErkJggg==)
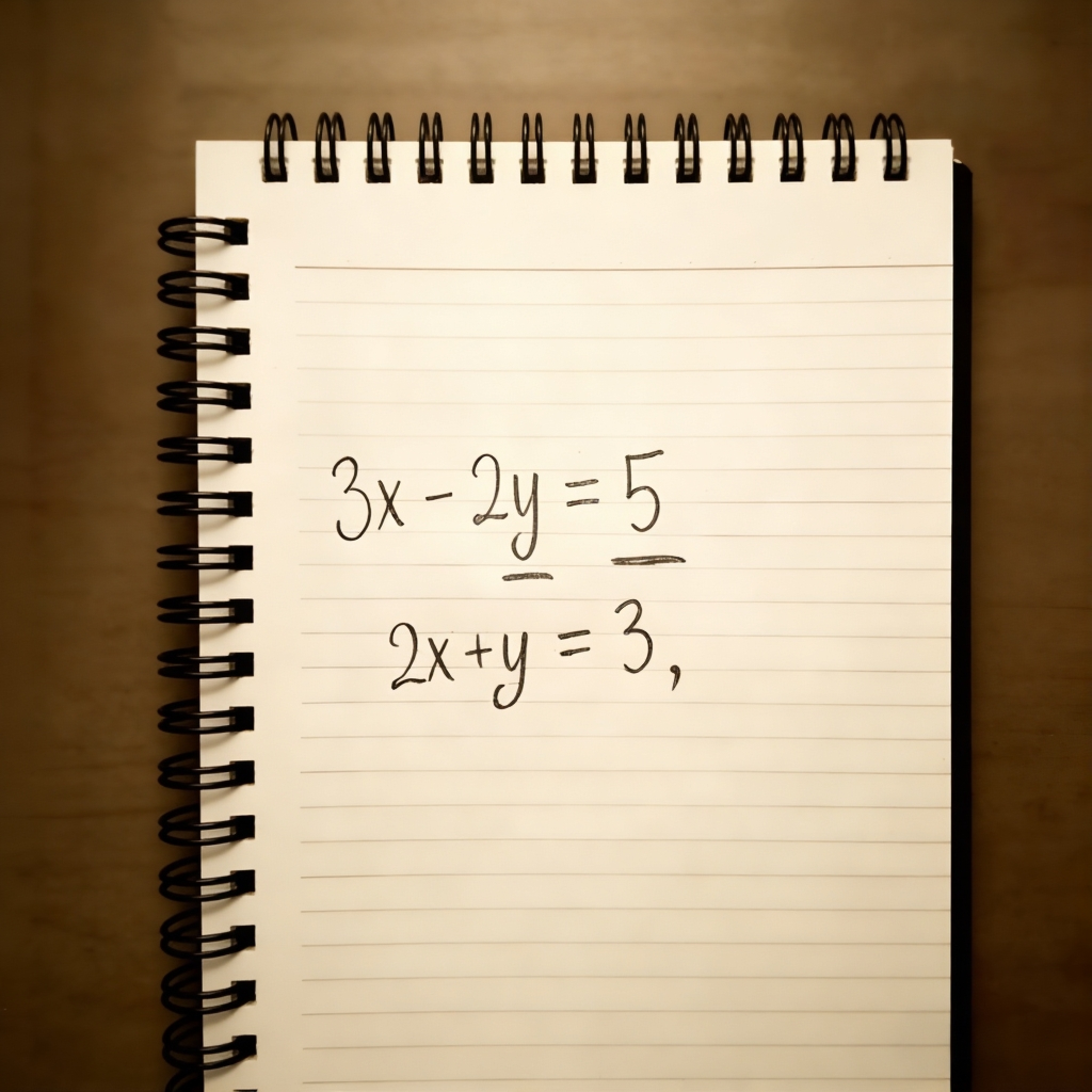
什么是方程？
方程是含有未知量的等式，解方程是为了求出未知数，在未知数和已知数之间建立起来的等式关系。常见的方程类型包括线性方程、二次方程、三角方程、对数方程和立方方程。
方程广泛应用于数学、物理、工程、经济学等多个领域，是理解现实世界问题和解决实际问题的重要工具。
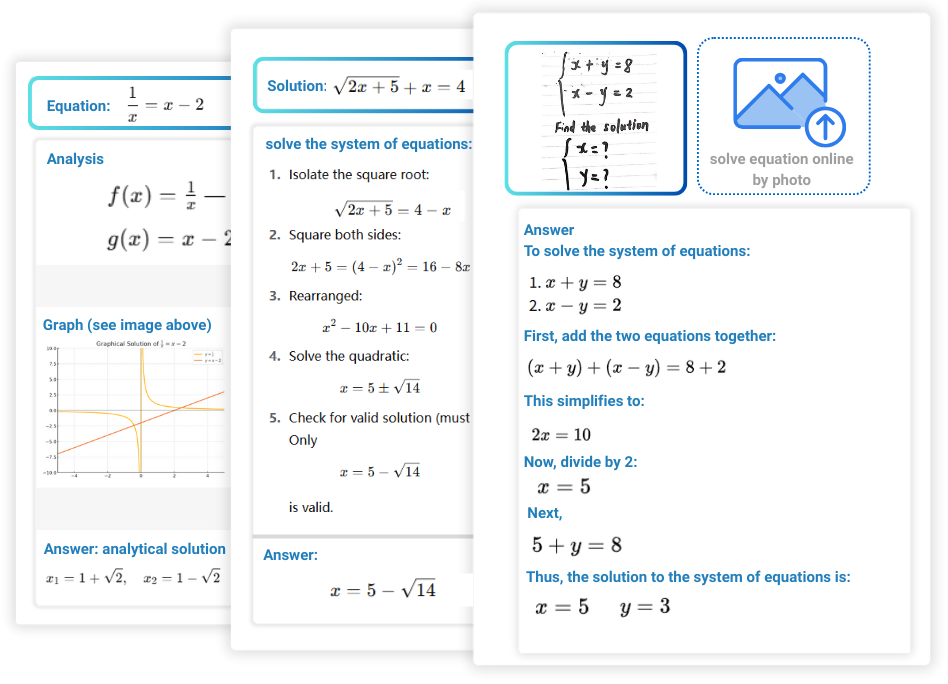
什么是方程计算器？
方程计算器是一种AI解决数学问题的工具，它通过算法分析，帮助用户快速、准确地求解各种类型的方程和方程组，用户可以输入方程，或直接上传包含方程的照片，计算器会自动识别并应用标准的数学方法进行求解，并以逐步推导的形式展示详细过程。
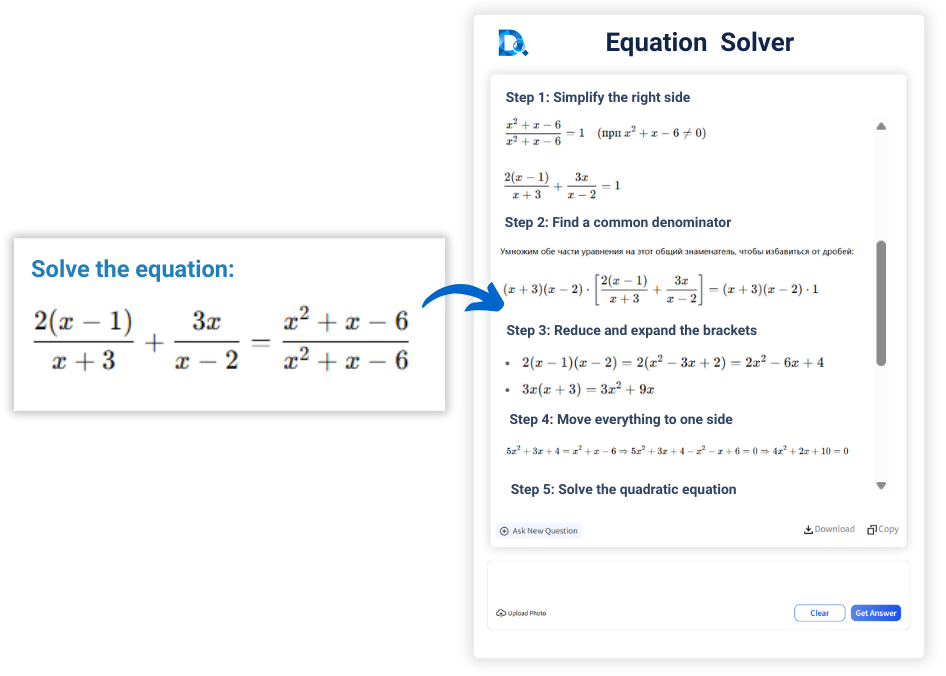
如何求解方程？
求解方程传统上需要手动列式、变换和运算，如使用因式分解法、判别式法、高斯消元法等。对于高次方程或复杂非线性系统，则需要更高级的数学方法和数值计算技术。
使用在线方程计算器，只需简单上传方程照片或直接输入方程，AI方程式计算器即可快速给出准确的答案，除此之外为了让用户更容易理解，方程式计算器会模拟人类解题思路，如消元法、代入法、求根公式等给出详细的解题步骤。
方程计算器如何工作？
方程计算器基于先进的AI数学引擎，结合代数、数值分析和算法优化技术工作。
当用户输入或上传方程时，系统会自动进行格式识别，判断方程类型（如线性、二次、三角、对数等），并根据适用的方法选择最佳求解路径：
对于线性方程和方程组，通常采用高斯消元、矩阵方法进行快速求解；
对于二次方程，使用判别式公式（求根公式）一步步推导出答案；
对于三角、对数、立方方程，应用标准变换技巧、因式分解或数值近似；
对于复杂非线性系统，调用数值逼近算法或高级计算方法进行求解。
该方程求解器提供最终答案并显示逐步解决方案，以帮助用户理解数学原理。
方程计算器的功能
在线快速、无错误地解决方程式，使用照片或手动，支持所有类型和逐步分析。
拍照解题
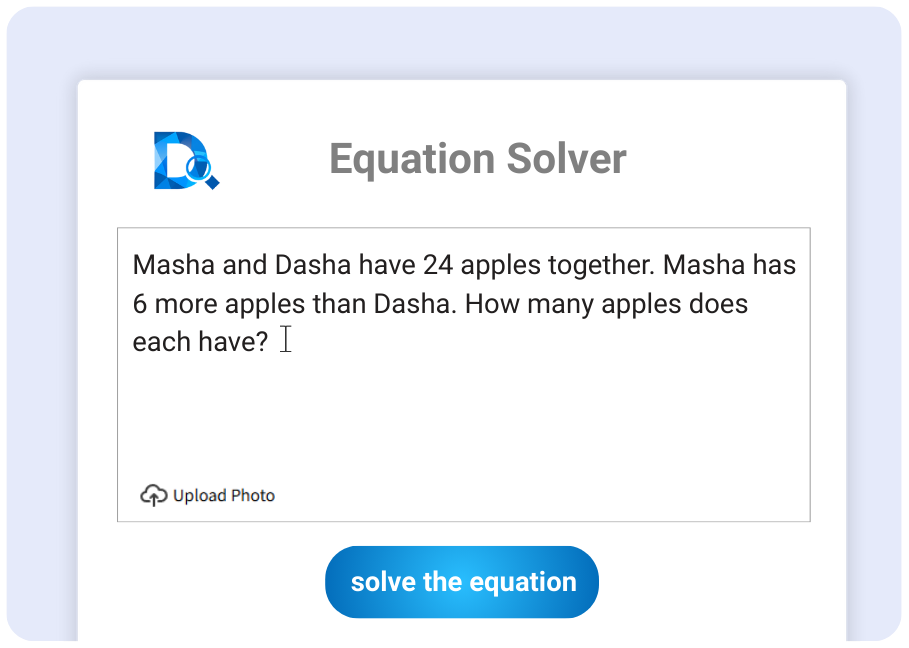
手动输入
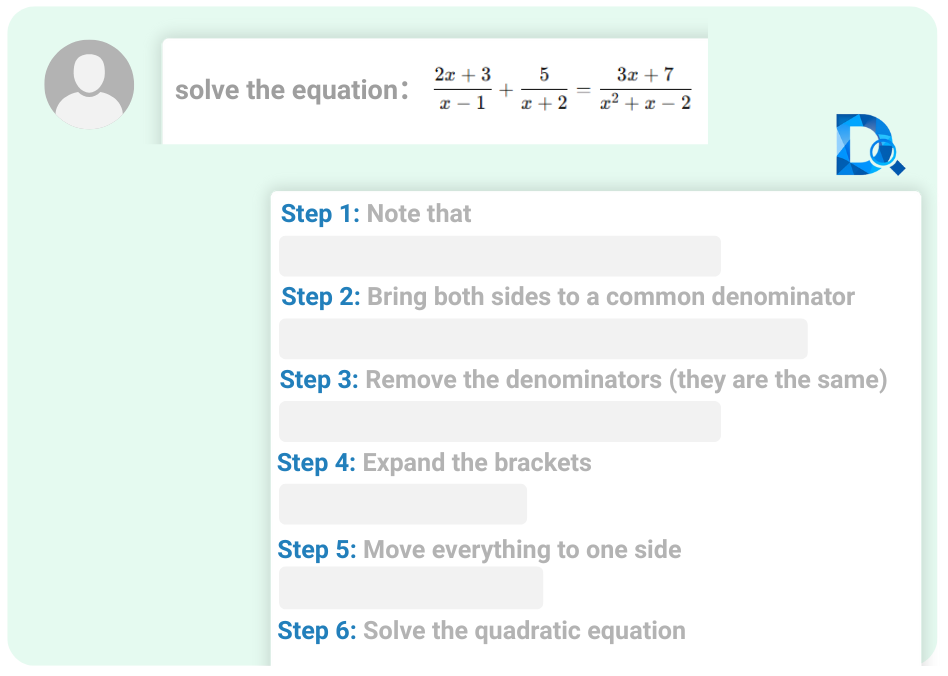
逐步解析
多类型方程支持
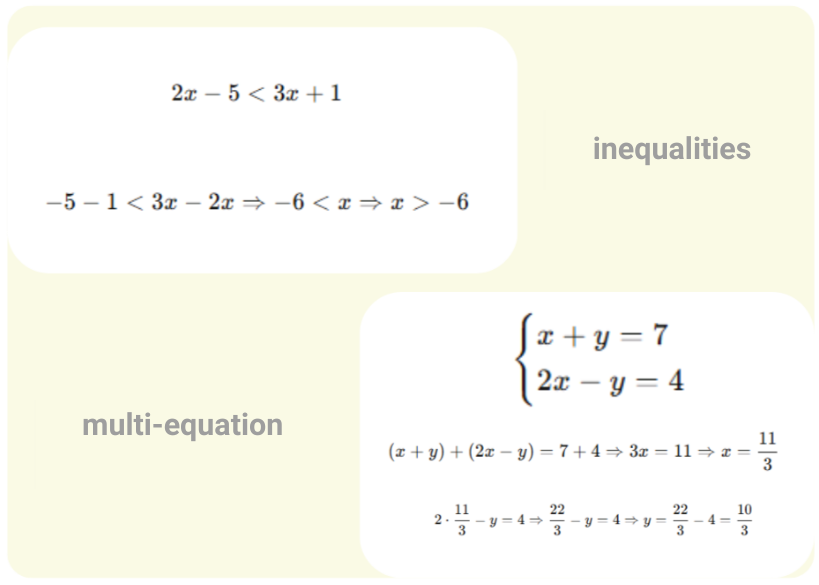
不等式与方程组求解
移动端优化
随时随地可用的方程计算器
移动便捷在线解方程工具，支持照片手动输入和分步分析。
学生作业
考前复习
课堂辅助
复杂验证
教学批改
自主学习
支持的方程类型
我们的方程计算器可以求解以下类型的数学方程。无论方程式多么复杂，您都能获得详细的分步解答。
| 方程类型 | 通用形式 | 解答特点 |
|---|---|---|
| 线性方程 | ax + b = 0 | 一个根，通过重新排列和除法求解 |
| 二次方程 | ax² + bx + c = 0 | 二次方程公式，至多两个解 |
| 四次方程 | x⁴ + bx² + c = 0 | 使用变量替换法求解 |
| 多项式方程 | aₙxⁿ + ... + a₀ = 0 | 至多n个实或复根 |
| 对数方程 | log_b(f(x)) = g(x) | 通过重写为f(x) = b^g(x)求解 |
| 指数方程 | a^{f(x)} = b^{g(x)} | 对两边进行对数变换 |
| 根式方程 | √f(x) = g(x) | 对两边平方并检查定义域 |
| 绝对值方程 | |f(x)| = g(x) | 两个情况：f(x)=g(x)和f(x)=–g(x) |
| 三角函数方程 | sin(x), cos(x), ... | 使用周期性和恒等式 |
| 复数方程 | f(z) = 0 | 复平面中的解 |
| 矩阵方程 | AX = B | 线性代数方法，逆矩阵 |
| 有理方程 | P(x)/Q(x) = 0 | 检查定义域并找到有理根 |
| 楼层函数方程 | ⌊f(x)⌋ = g(x) | 在整数区间内求解 |
| 根基构造 | f(x) = (x − r₁)... | 从已知根构建多项式 |
| 点基构造 | f(x) through (x₁, y₁)... | 插值方法 |
| 数值方法 | f(x) = 0 | 近似根的寻找（例如，牛顿法） |
| 微分方程 | y', y'' = f(x) | 通过解法方法找到函数y(x) |
如何使用方程计算器？
- 1
打开网站，进入方程计算器页面。
- 2
上传照片或直接输入方程式。
- 3
点击开始求解，AI自动解算。
- 4
查看逐步解答或继续追问。
在线方程计算器适合哪些人
快速准确地解决从小学到大学水平的数学方程式，并全面支持小学到大学的国家评估和标准化考试。
小学阶段学生
用于基础数学训练，培养代数与方程的早期思维能力。
初高中生
此工具可帮助学生解决初中和高中考试中常见的数学问题，包括代数、函数和三角函数。非常适合准备中考和高考的数学考试。
大学生和研究生
适用于高等数学、微积分、线性代数课程，轻松应对复杂函数与多元方程。
数学自学者
适合想独立提升数学思维与逻辑结构能力的成年人。
教师与辅导员
教师提供备课参考、标准解法与学生答题反馈辅助，提升教学效率。
留学生
涵盖研究生入学考试及海外标准考试中的数学部分，快速验证答案，节省备考时间。
为什么使用我们的方程计算器
完全免费使用
无登录、无广告，免费在线解方程，无任何隐藏费用。
解答精准可靠
AI智能算法驱动，准确处理各种方程，包括多步运算与复杂结构。
操作简单高效
支持输入或上传含变量、符号的方程式，轻松获取完整解析过程。
支持多语言方程
识别八国语言，适配全球主流数学考试。
无需下载，随时解题
无需下载App，直接网页版操作。
多类型方程全覆盖
支持线性、二次、三角、对数、指数、不等式及方程组求解，适应从基础到高阶的学习需求。
用户反馈
常见问题 (FAQs)
不同类型的方程适用不同的解法：
代入法 – 适合解两个未知数的方程组；
消元法 –
用于消除变量，求出特解；
配方法 / 求根公式 – 适合一元二次方程；
图像法 / 数值法 –
适用于高阶方程或无解析解的问题；
方程求解器 –
适合快速解决结构复杂、步骤繁琐的问题，并展示完整过程。
配方法是解决一元二次方程 ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0 的技巧。通过将表达式整理为完整平方的形式，如 (x+d)2=e(x + d)^2 = e(x+d)2=e，可更直观地求出变量的值。特别适合结构不整齐、系数较难处理的二次方程。
解方程最重要的原则是：保持等式两边平衡。
无论是加、减、乘、除，只要对一边操作，也必须对另一边做相同处理。否则方程的本质（等式）将被破坏，解也会出错。
步骤如下：
1. 移项: 将未知数移至一边，常数项移至另一边；
2. 化简:
合并同类项，简化表达式；
3. 求解: 通过加减、乘除，整理为 x=数值x = 数值x=数值 的形式；
始终确保每一步操作都同时作用于方程两边。
化简是解题的基础操作，通常包括：
1. 去除括号；
2. 合并同类项（如 3x+2x=5x3x + 2x =
5x3x+2x=5x）；
3. 遵循 PEMDAS 运算顺序（括号 → 指数 → 乘除 → 加减），使方程更整洁，方便求解。
1. 简化两边: 合并项、去括号；
2. 隔离未知数: 将变量项移至一侧；
3. 求出变量:
用相反运算简化系数，得到最终结果。
只需输入方程，系统自动识别变量和结构，使用智能算法（如代数推导、数值计算等）进行求解，并展示详细步骤与每一步推理依据。非常适合用于学习理解、作业检查或复杂题验证。
📘 完整的支持数学函数列表
探索Decopy AI方程计算器中可以使用的语法和符号。
📂 点击查看支持的函数
| 函数 | 描述 |
|---|---|
| abs(x) | x的绝对值 |
| arccos(x) | x的反余弦 |
| arccosh(x) | 双曲反余弦 |
| arcsin(x) | x的反正弦 |
| arcsinh(x) | 双曲反正弦 |
| arctg(x) | x的反正切 |
| arctgh(x) | 双曲反正切 |
| asec(x) | x的反正割 |
| asech(x) | 双曲反正割 |
| cbrt(x) | x的立方根 |
| ceiling(x) | 向上取整到最近的整数 |
| chi(x) | 双曲余弦积分 |
| cos(x) | x的余弦 |
| cosh(x) | 双曲余弦 |
| cosec(x), csc(x) | x的余割 |
| ctg(x) | x的余切 |
| diracdelta(x) | 狄拉克δ函数 |
| e | 欧拉数 ≈ 2.71828 |
| exp(x) | 指数函数 (e^x) |
| factorial(x), x! | x的阶乘 |
| floor(x) | 向下取整到最近的整数 |
| gamma(x) | 伽马函数 |
| heaviside(x) | 海维塞阶跃函数 |
| i | 虚数单位 (√-1) |
| lambertw(x) | 朗伯特W函数 |
| ln(x), log(x) | 自然对数 |
| log(a,x) | 以a为底的对数 |
| oo | 无穷大 |
| pi | 圆周率 ≈ 3.14159 |
| sec(x) | x的正割 |
| sech(x) | 双曲正割 |
| sign(x) | 数的符号 |
| sin(x) | x的正弦 |
| sinh(x) | 双曲正弦 |
| sqrt(x) | 平方根 |
| sqr(x), x^2 | x的平方 |
| Si(x), Ci(x), Shi(x), Chi(x) | 积分三角和双曲函数 |
| tg(x), tan(x) | 正切 |
| tgh(x) | 双曲正切 |
| x + y, x - y | 加法、减法 |
| x * y, x / y | 乘法、除法 |
| x^n, pow(x,n) | 幂运算 |