学生
图形计算器对从小学到大学的学生都有益。它帮助他们掌握数学概念，培养解决问题的技能。
图形计算器
图形计算器能够解决方程并绘制函数的图形，帮助您直观且准确地理解函数的变化模式。
什么是图形计算器？
图形计算器是一款功能强大、技术先进的绘图工具，它能帮助我们绘制函数图像、进行复杂计算和数据分析，通过参数调整影响图形的变换，让数学学习与研究变得更加直观、高效和有趣。
代替复杂的手动绘图
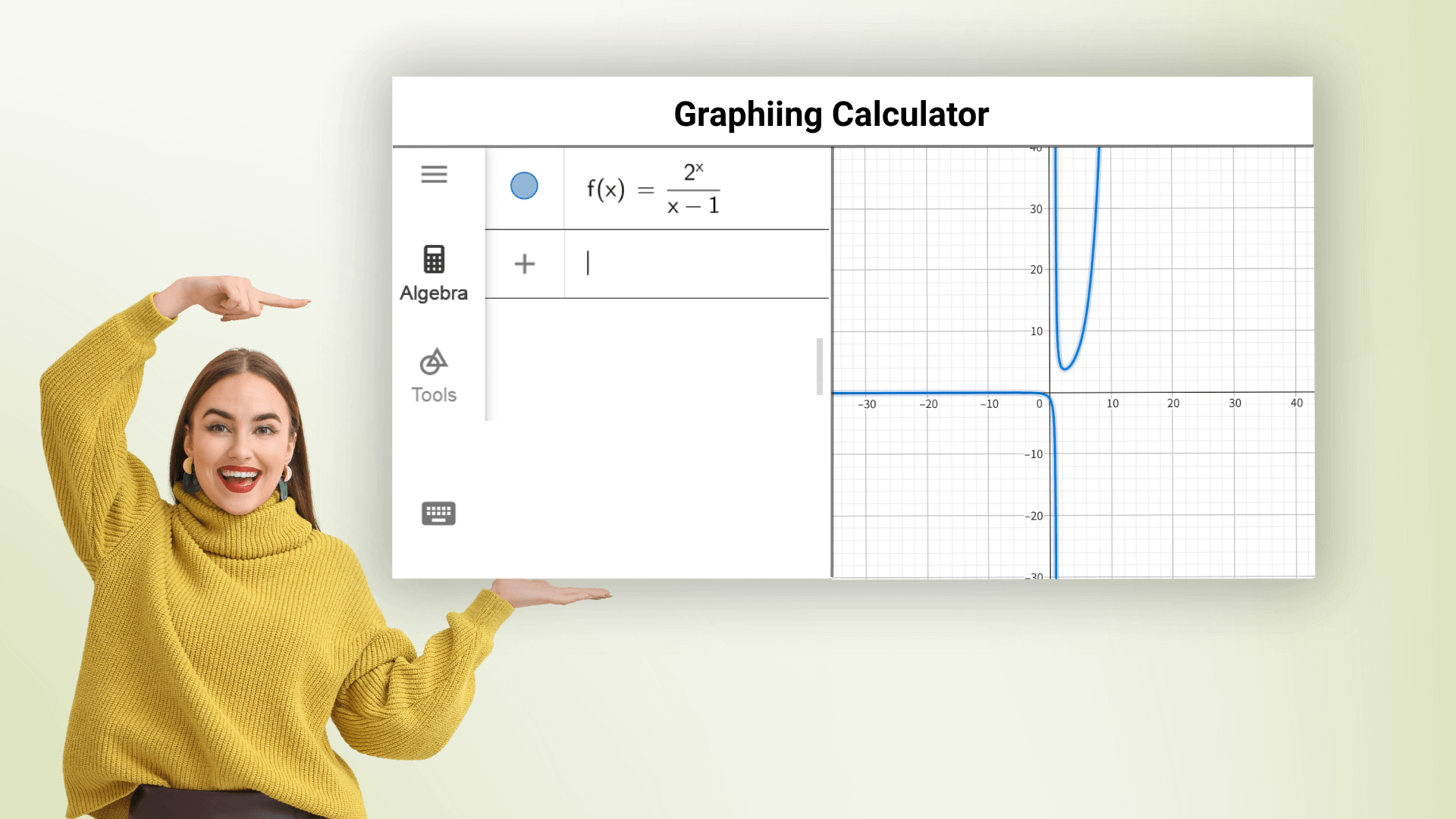
图形计算器可以绘制多种类型的函数图像，如直线、抛物线、三角函数、对数函数等，并能同时绘制多个方程图像，通过不同颜色进行区分。您只需输入函数表达式，就能快速得到精准的图像，直观地观察函数的变化趋势和特点。 我们的在线图形计算器让每个人都能成为数学高手，告别复杂的计算过程。
丰富的科学计算方式
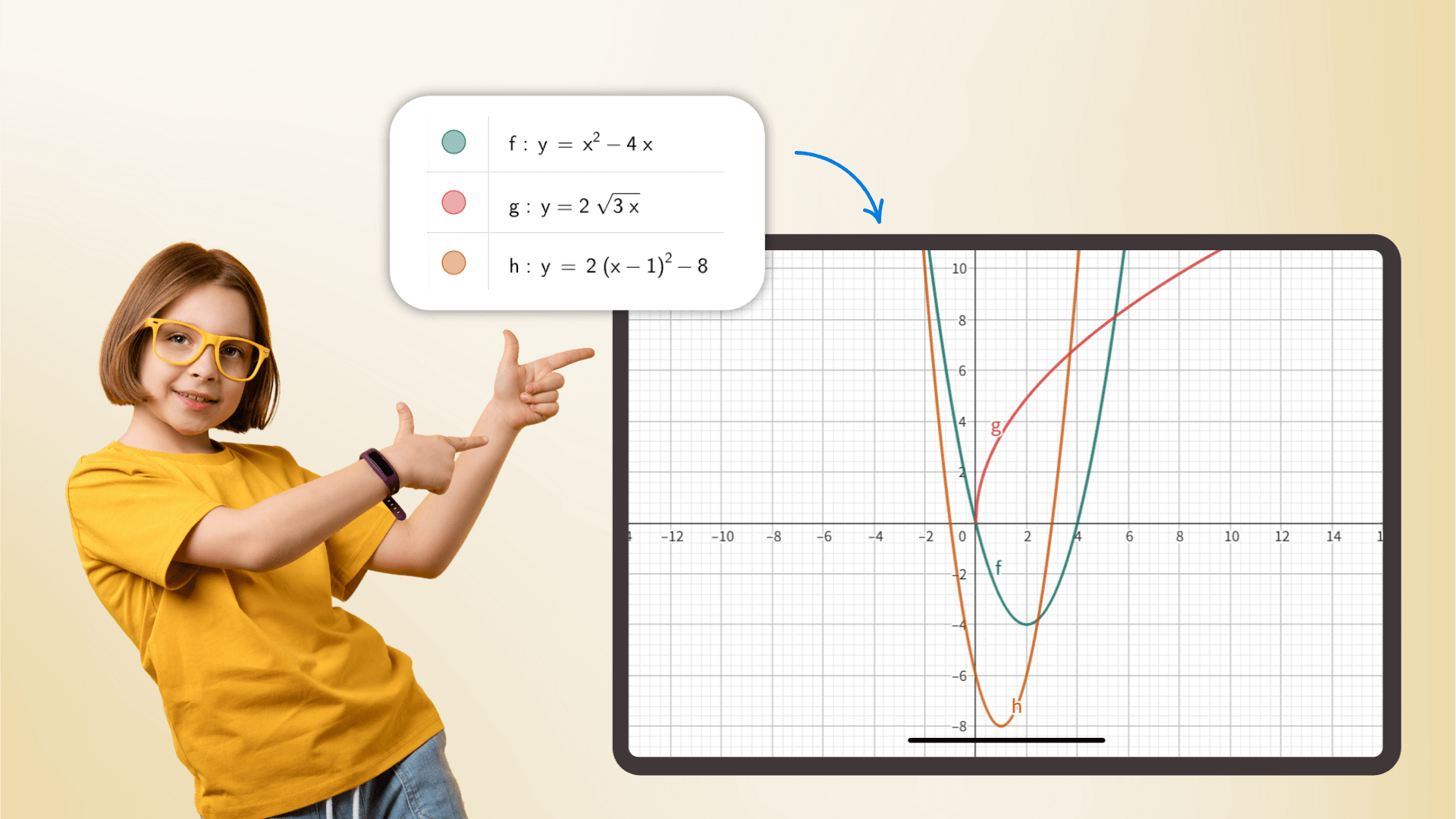
作为一款科学计算器，它能够处理从基础算术到高级数学微积分、概率统计等所有内容。凭借精准的计算，它是学生和研究人员不可或缺的助手，能够提升学术和专业领域的效率。
智能交互式绘图
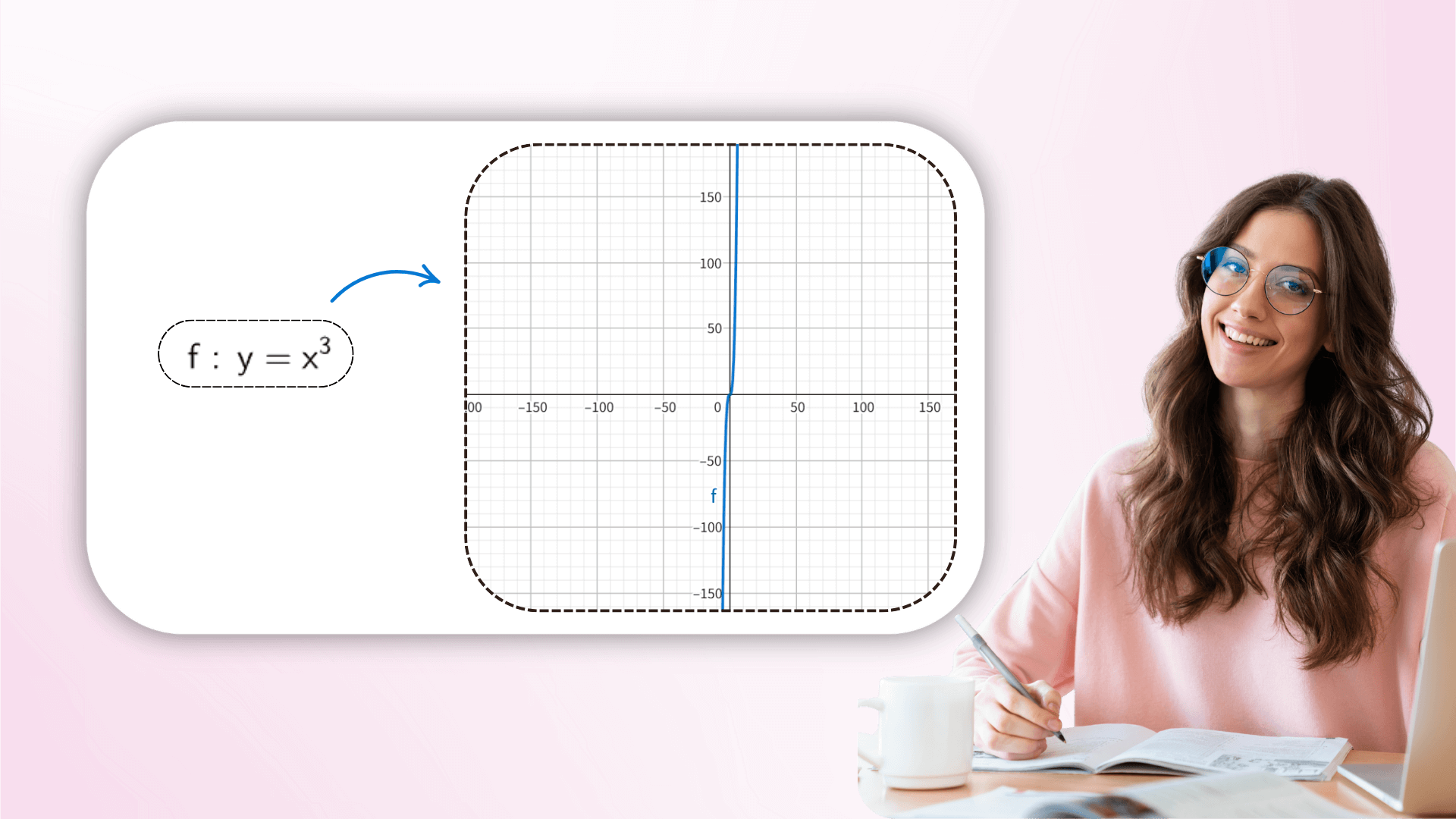
通过实时调整参数值，用户可以观察图像动态变化，从而了解系数如何影响函数几何形状，从线性平移到复杂变换，将抽象公式与视觉联系起来，这种交互式探索可以加深对数学方程的理解。
图形计算器的功能
交互式绘图
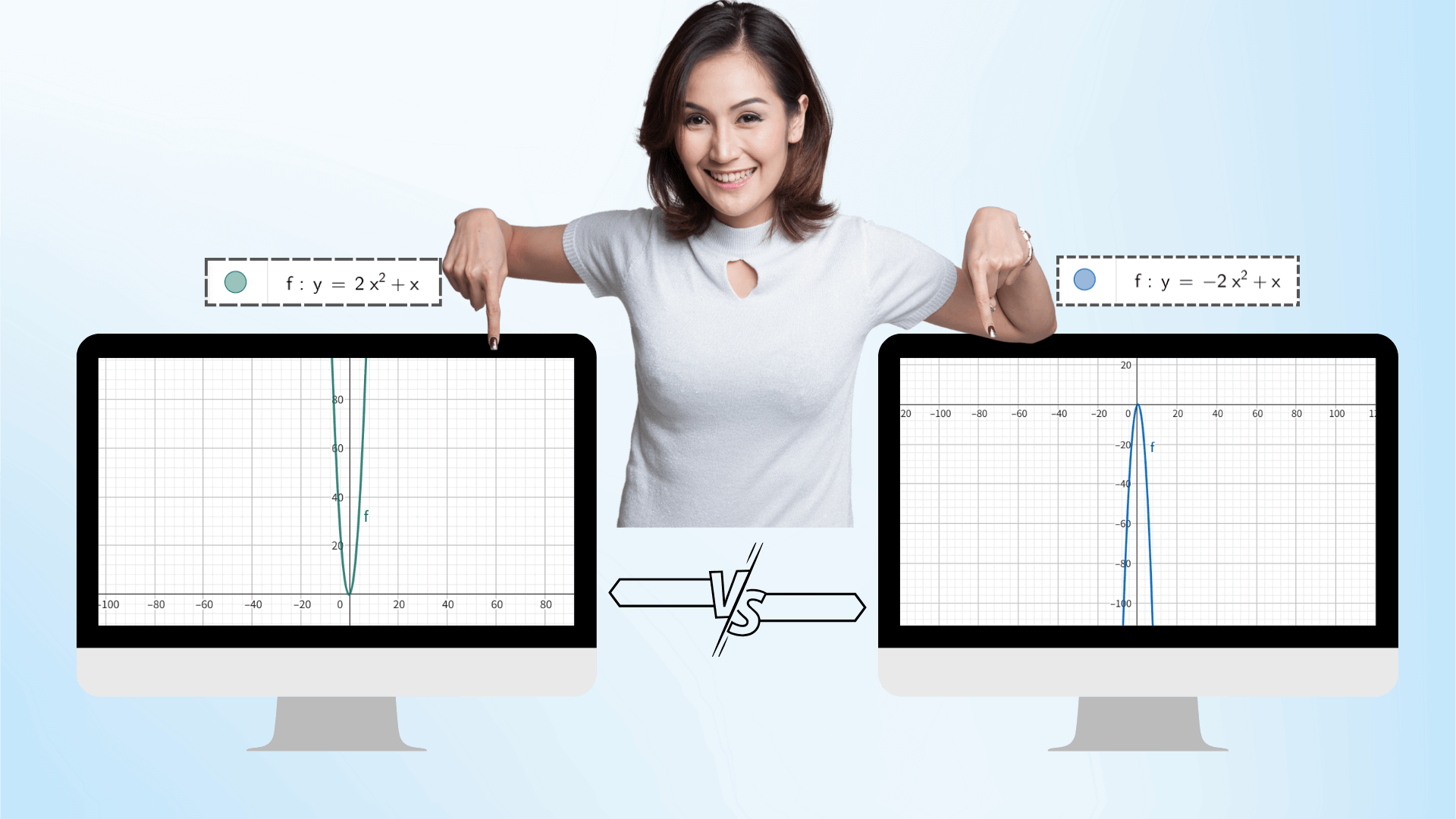
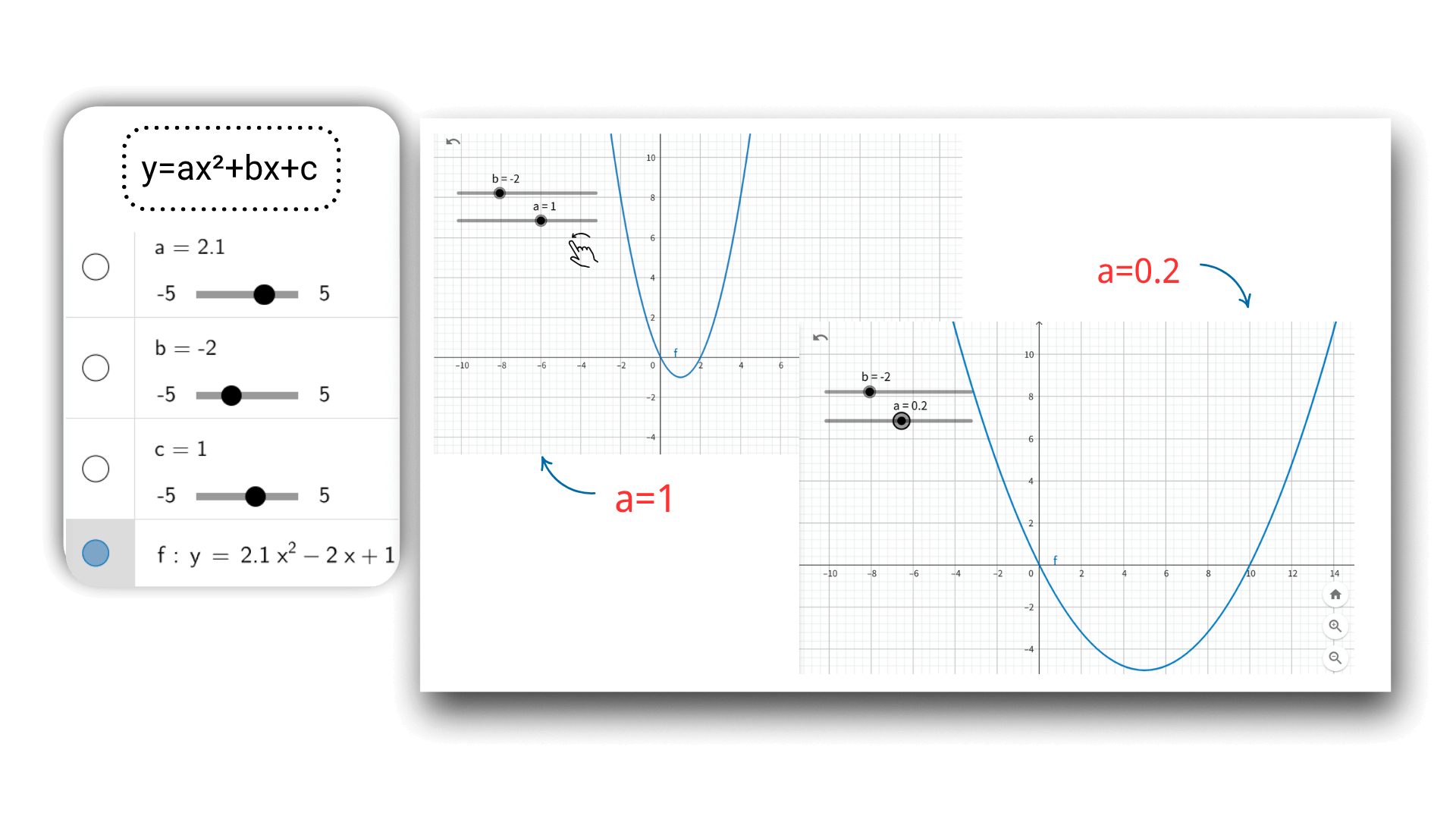
利用 AI 绘图技术，输入函数后即可通过滑块动态调节参数，例如二次函数的 a、b、c，图像如动画般实时变形，坐标数据同步更新，直观揭示参数变化对图像的影响，更好地理解数学概念之间的联系。
智能数据分析
采用先进的计算算法，确保每一次计算结果都具有极高的精度，为您的数学工作提供可靠的数据支持。只需在我们的图像计算器上输入数组，即可一键生成各种图像。
自动纠错与建议
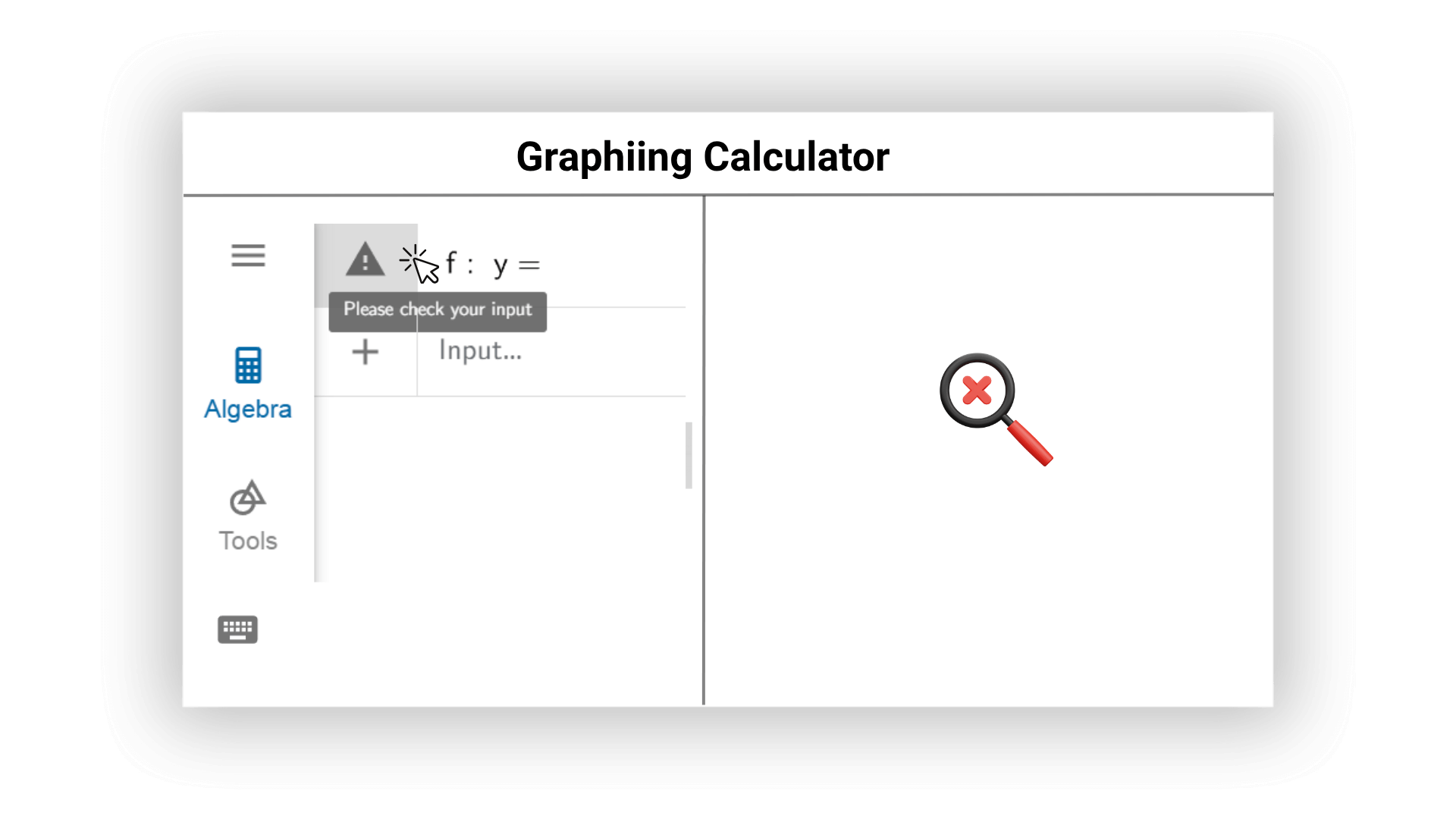
我们的AI图形计算器能实时在线检查数学表达式中可能存在的错误，并主动给出修改建议。语法上的问题和不合理的输入，AI都能及时提醒用户，保证计算结果准确且运算效率高，避免图像和结果出错。
图形计算器的应用场景
数学教育
图形计算器是学生学习数学的得力助手，从中学到大学，无论是代数、几何、微积分还是统计学课程，都能帮助学生更好地理解和掌握数学知识，提高学习效率和成绩。教师可以利用它进行教学演示，制作生动形象的教学课件，激发学生的学习兴趣和积极性。
科学研究
图形计算器为科研人员提供了强大的数学工具，方便他们进行数据处理、实验分析、模型建立和理论验证等工作。在物理、化学、生物、工程等各个科学领域，都能借助图形计算器快速准确地完成复杂的数学运算和数据分析，辅助科研工作的顺利开展。
商业与数据分析
利用图形计算器绘制供需曲线、复利增长模型等，分析边际成本与收益函数交点，可视化展示市场饱和趋势，辅助企业决策。
如何使用图形计算器？
Step 1
输入数学表达式
在输入区输入您需要绘制的函数表达式或要分析的数据，AI 图形计算器即刻开始处理它。
Step 2
即时生成图表
运行计算或绘图后，您可以立即看到生成的图像、数据和计算结果。
Step 3
交互式操作
调整参数或对其进行进一步的分析和解读，图标会实时更新。
谁能使用我们的图形计算器？
- 学生
- 教师
- 研究人员
- 数据分析师
- 软件工程师
- 设计师
教师
数学教师可以使用图形计算器来创建教学材料，展示概念和解决问题的过程，从而提高教学的有效性和互动性。
研究人员
各个领域的研究人员都依赖图形计算器来进行复杂的数学计算和数据分析。在线图形计算器提供精确的结果，推动研究的进行。
数据分析师
使用图形计算器绘制供需曲线、复利增长模型等，分析边际成本与收益函数交点，视觉化展示市场饱和趋势，辅助企业决策。
软件工程师
图形计算器帮助软件工程师可视化滤波算法并优化渲染参数，确保像素完美的功能性能。
建筑设计师
对于建筑设计师，图形计算器是参数设计的强大工具，输入曲线方程生成函数/位移图，视觉验证结构力学，并缩短设计周期。
Decopy 图形计算器的功能优势
完全免费使用
所有功能都无需注册或付费，一用到底。
高精度算法
计算矩阵行列式、积分等高级问题时也保持高精度，避免科研误差。
数据私密安全
运算完全在浏览器本地完成，数据无上传，页面关闭即清除。
随时可用
无需下载安装，手机、电脑都可即刻使用。
无广告打扰
专注学习本质，无弹窗，无广告，提升专注度。
全场景支持
无论是学业、科研、办公还是工程应用，我们都能满足您的图形化运算需求。
用户反馈
Sarah Johnson
大学生
Robert Thompson
数学教师
David Wilson
金融分析师
常见问题 (FAQs)
您无需注册账号或下载任何软件，只需在浏览器中输入我们的网址，即可直接开始使用这个功能强大的图形计算器，立即体验其便捷性。
尽管我们的图形计算器完全免费，但并未因此削减或限制任何核心功能。您同样可以使用强大的绘图、计算、数据分析等功能，无需担心付费门槛。我们致力于为所有用户提供便捷、高效的数学计算工具。
我们高度重视用户数据的安全与隐私。您的所有计算、绘图和输入的数据不会被上传或保存到我们的服务器上。您可以放心使用，无需担心数据泄露或被滥用的风险。
要在 AI 图形计算器中输入函数，只需在主页提供的输入框中输入公式即可。例如，您可以输入“y=2x^2”或“f(x) = sin(x)”之类的表达式。AI 图形计算器将自动处理您的输入并显示图形。就是这么简单！
是的，AI 图形计算器能够处理各种数学函数，从简单的线性方程到更复杂的函数，例如积分、导数和多变量方程。它设计用于处理基础数学和高级数学，非常适合学生、专业人士以及任何需要将数学函数可视化的人士。
是的，它完全可以在移动设备上使用。无论您使用的是智能手机还是平板电脑，都可以轻松访问网站并使用该工具绘制函数图形。该工具针对所有屏幕尺寸进行了优化，因此您可以在移动设备上享受相同的特性和功能。
↑